Problemas de valor inicial
Observamos técnicas para integrar una gran variedad de funciones que involucran productos, cocientes y composiciones más adelante en el texto. Aquí pasamos a un uso común para los antiderivadas que surge a menudo en muchas aplicaciones: resolver ecuaciones diferenciales.
Una ecuación diferencial es una ecuación que relaciona una función desconocida y una o más de sus derivadas. La ecuación


es un ejemplo simple de una ecuación diferencial. Resolver esta ecuación significa encontrar una función y cuya primera derivada sea igual a f(x). Por lo tanto, las soluciones de esta ecuación son las antiderivadas de f. Si F es una antiderivada de f, cada función de la forma y = F (x) + C es una solución de esa ecuación diferencial. Por ejemplo, las soluciones de


son dadas por


A veces estamos interesados en determinar si una curva de solución particular pasa por un cierto punto (x0, y0), es decir, y(x0) = y0. El problema de encontrar una función y que satisfaga una ecuación diferencial


con la condición adicional


es un ejemplo de un problema de valor inicial. La condición y(x0) = y0 se conoce como condición inicial.
Por ejemplo, buscando una función y que satisfaga la ecuación diferencial


y la condición inicial
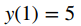
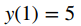
es un ejemplo de un problema de valor inicial. Dado que las soluciones de la ecuación diferencial son


para encontrar una función y que también satisfaga la condición inicial, necesitamos encontrar C tal que
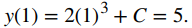
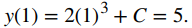
A partir de esta ecuación, vemos que C = 3, y concluimos que
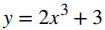
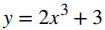
es la solución de este problema de valor inicial como se muestra en la siguiente gráfica.


Los problemas de valor inicial surgen en muchas aplicaciones como veremos en los videos sobre los siguientes ejercicios resueltos.

¿Alguna vez ha considerado incluir un poco más que solo sus artículos? Quiero decir, lo que dices es fundamental y todo. ¡Pero piense si agregó algunas fotos o videos geniales para dar más a sus publicaciones, “pop”! Su contenido es excelente, pero con fotos y videos, este blog podría ser uno de los mejores en su nicho. Excelente blog!
Poco a poco iré enriqueciendo este sitio web incluyendo videos e imágenes sobre la solución de problemas y ejercicios!