Ejercicios propuestos para el capítulo 9.5.6
En los ejercicios 1 a 17, encuentre la solución general, dado que y1 satisface la ecuación complementaria. Como subproducto, encuentre un conjunto fundamental de soluciones de la ecuación complementaria.
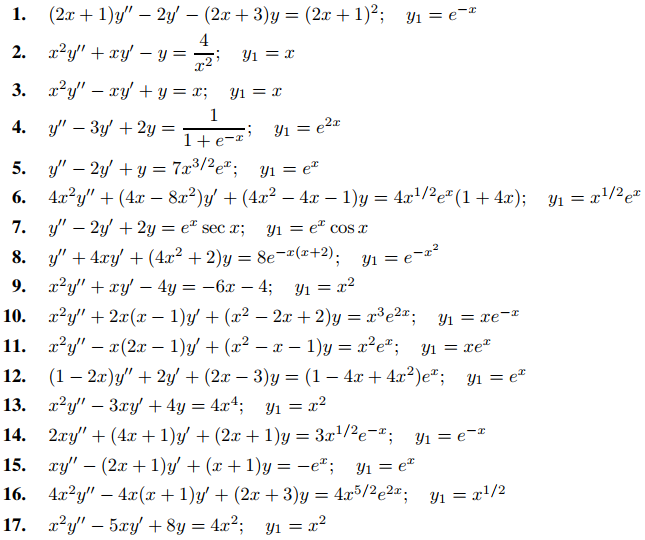
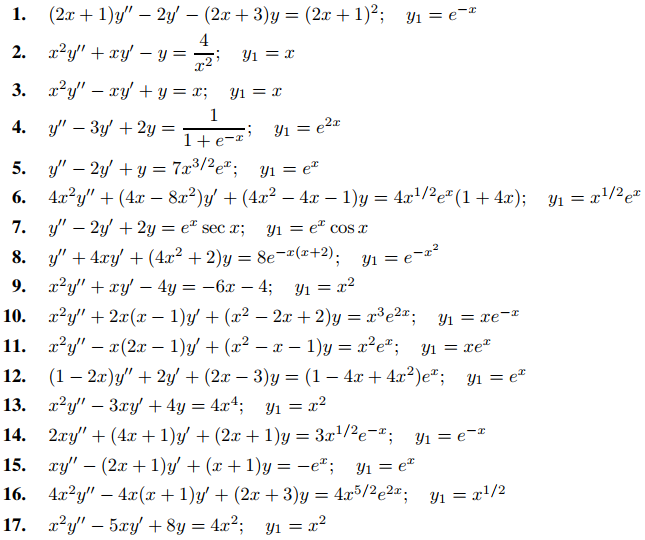
En los ejercicios 18 a 30 encuentre un conjunto fundamental de soluciones, dado que y1 es una solución.
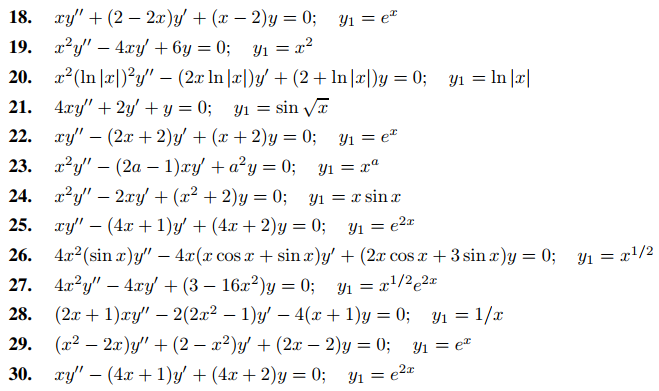
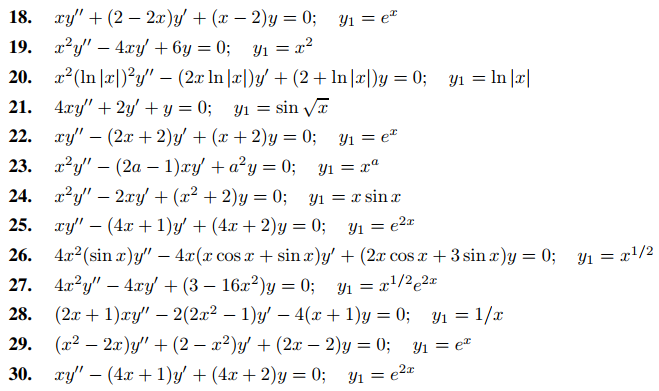
En los Ejercicios 31 a 33 resuelva el problema del valor inicial, dado que y1 satisface la ecuación complementaria.
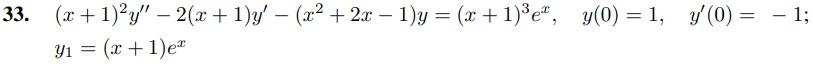
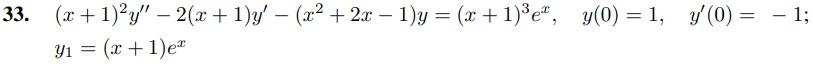
En los Ejercicios 34 y 35 resuelva el problema de valor inicial y grafique la solución, dado que y1 satisface la ecuación complementaria.
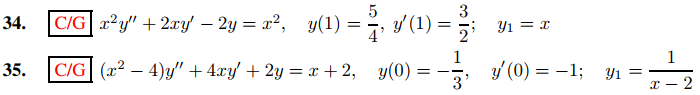
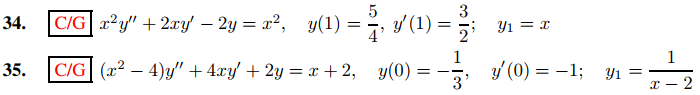
36. Suponga que p1 y p2 son continuos en (a, b). Sea y1 una solución de
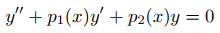
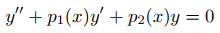
que no tiene ceros en (a, b), y sea x0 perteneciente (a, b). Utilice la reducción de orden para mostrar que y1 y
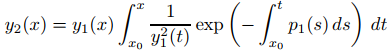
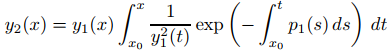
Forme un conjunto fundamental de soluciones de (A) en (a, b). (NOTA: este ejercicio está relacionado con el ejercicio 9.)
37. La ecuación de primer orden no lineal
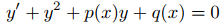
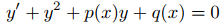
es una ecuación de Riccati. (Consulte el ejercicio 9.2.4.55.) Suponga que p y q son continuas.
(a) Demuestre que y es una solución de (A) si y solo si y = z′/z, donde
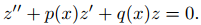
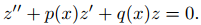
(b) Demuestre que la solución general de (A) es
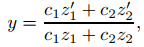
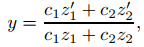
donde {z1, z2} es un conjunto fundamental de soluciones de (B) y c1 y c2 son constantes arbitrarias.
(c) ¿La fórmula (C) implica que la ecuación de primer orden (A) tiene una familia de soluciones de dos parámetros? Explica tu respuesta.
38. Utilice un método sugerido por el ejercicio 37 para encontrar todas las soluciones. de la ecuación dada.
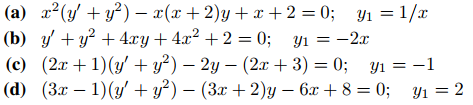
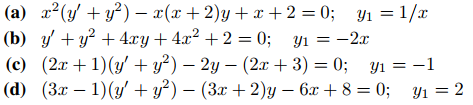
39. Utilice un método sugerido por el ejercicio 37 y reducción de orden para encontrar todas las soluciones de la ecuación, dado que y1 es una solución.
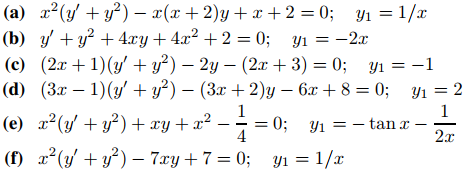
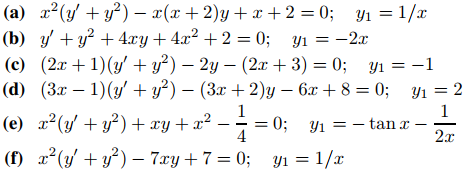
40. La ecuación no lineal de primer orden
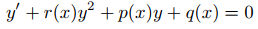
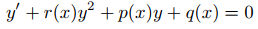
es la ecuación de Riccati generalizada. (Consulte el ejercicio 9.2.4.55.) Suponga que p y q son continuas y que r es derivable.
(a) Muestre que y es una solución de (A) si y solo si y = z′/rz, donde
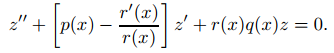
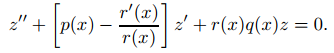
(b) Demuestre que la solución general de (A) es
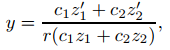
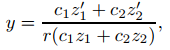
donde {z1, z2} es un conjunto fundamental de soluciones de (B) y c1 y c2 son constantes arbitrarias.
