| 10. Cálculo vectorial – Vectores en el espacio | 10.1 Vectores en el plano |

Ejercicios propuestos para el Capítulo 10.1

       Para los siguientes ejercicios, 1 a 10, considere los puntos P(−1, 3), Q(1, 5) y R(−3, 7). Determinar los vectores solicitados y expresar cada uno de ellos a. en forma de componente y b. utilizando los vectores unitarios estándar.

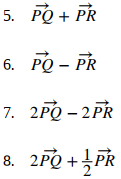
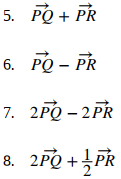
11. Un vector v tiene un punto inicial (−1, −3) y un punto terminal (2, 1). Encuentre el vector unitario en la dirección de v. Exprese la respuesta en forma de componentes.

12. Un vector v tiene un punto inicial (−2, 5) y un punto terminal (3, −1). Encuentre el vector unitario en la dirección de v. Exprese la respuesta en forma de componentes.

13. El vector v tiene un punto inicial P(1, 0) y un punto terminal Q que está en el eje y y arriba del punto inicial. Encuentre las coordenadas del punto terminal Q de manera que la magnitud del vector v sea √5.

14. El vector v tiene un punto inicial P(1, 1) y un punto terminal Q que está en el eje x y a la izquierda del punto inicial. Encuentre las coordenadas del punto terminal Q tales que la magnitud del vector v sea √10.

       

       Para los siguientes ejercicios, use los vectores a y b dados.

1. Determine la suma vectorial a + b y expresela tanto en la forma componente como usando los vectores unitarios estándar.
2. Encuentre la diferencia vectorial a − b y expresela tanto en la forma de componente como usando los vectores unitarios estándar.
3. Verifique que los vectores a, b y a + b,  y  a, b y a − b satisfacen, respectivamente, la desigualdad del triángulo.
4. Determine los vectores 2a, −b  y  2a − b. Exprese los vectores tanto en la forma de componentes como utilizando vectores unitarios estándar.

17. Sea a un vector de posición estándar con punto terminal (−2, −4). Sea b un vector con punto inicial (1, 2) y punto terminal (−1, 4). Encuentre la magnitud del vector −3a + b −  4i + j.

18. Sea a un vector de posición estándar con punto terminal en (2, 5). Sea b un vector con punto inicial (−1, 3) y punto terminal (1, 0). Encuentre la magnitud del vector a − 3b + 14i − 14j.

19. Sean u y v dos vectores distintos de cero que no son equivalentes. Considere los vectores a = 4u + 5v  y  b = u + 2v definidos en términos de u y v. Encuentre el escalar λ tal que los vectores a + λb  y  u − v sean equivalentes. 

20. Sean u y v dos vectores distintos de cero que no son equivalentes. Considere los vectores a = 2u − 4v  y  b = 3u − 7v definidos en términos de u y v. Encuentre los escalares α y β tales que los vectores αa + βb  y  u − v sean equivalentes.

21. Considere el vector a(t) = ⟨cost, sent⟩ con componentes que dependen de un número real t. A medida que varía el número t, los componentes de a(t) también cambian, dependiendo de las funciones que los definen.

1. Escriba los vectores a(0) y a(π) en forma de componentes.
2. Demuestre que la magnitud ∥a(x)∥ del vector a(x) permanece constante para cualquier número real x
3. A medida que x varía, demuestre que el punto terminal del vector a(x) describe un círculo centrado en el origen del radio 1.

 

22. Considere el vector a(x) = ⟨x, √(1 − x²)⟩ con componentes que dependen de un número real x∈[−1, 1]. A medida que varía el número x, los componentes de a(x) también cambian, dependiendo de las funciones que los definen.

1. Escriba los vectores a(0) y a(1) en forma de componentes.
2. Demuestre que la magnitud ∥a(x)∥ del vector a(x) permanece constante para cualquier número real x
3. A medida que x varía, demuestre que el punto terminal del vector a(x) describe un círculo centrado en el origen de radio 1.

 

23. Muestre que los vectores a(t) = ⟨cost, sent⟩ y a(x) = ⟨x, √(1 − x²)⟩ son equivalentes para x = 1  y  t = 2kπ, donde k es un número entero.

24. Muestre que los vectores a(t) = ⟨cost, sent⟩  y  a(x) = ⟨x, √(1 − x²)⟩ son opuestos para x = r  y  t = π + 2kπ, donde k es un número entero.

 

       Para los siguientes ejercicios, encuentre el vector v con la magnitud dada y en la misma dirección que el vector u.

       Para los siguientes ejercicios, encuentre la forma componente del vector u, dada su magnitud y el ángulo que forma el vector con el eje x positivo. Dé respuestas exactas cuando sea posible.

      Para los siguientes ejercicios, se da el vector u. Encuentre el ángulo θ∈ [0, 2π) que forma el vector u con la dirección positiva del eje x, en sentido antihorario.

37. Sean a = ⟨a₁, a₂⟩, b = ⟨b₁, b₂⟩ y c = ⟨c₁, c₂⟩ tres vectores distintos de cero. Si a₁b₂ − a₂b₁ ≠ 0, entonces demuestre que hay dos escalares, α y β, tales que c = αa + βb.

38. Considere los vectores a = ⟨2, −4⟩, b = ⟨− 1,2⟩ y c = 0 Determine los escalares α y β tales que c = αa + βb.

39. Sea P(x₀, f (x₀)) un punto fijo en la gráfica de la función diferenciable f con un dominio que es el conjunto de números reales.

1. Determine el número real z₀ tal que el punto Q(x₀ + 1, z₀) esté situado en la recta tangente a la gráfica de f en el punto P.
2. Determine el vector unitario u con el punto inicial P y el punto terminal Q.

 

40. Considere la función f (x) = x⁴, donde x∈R.

1. Determine el número real z₀  tal que el punto Q(2, z₀) está situado en la recta tangente a la gráfica de f en el punto P(1, 1).
2. Determine el vector unitario u con el punto inicial P y el punto terminal Q.

 

41. Considere f  y  g dos funciones definidas en el mismo conjunto de números reales D. Sean a = ⟨x, f (x)⟩ y b = ⟨x, g(x)⟩ dos vectores que describen las gráficas de las funciones , donde x∈D. Demuestre que si las gráficas de las funciones f  y  g no se intersecan, entonces los vectores a y b no son equivalentes.

42. Encuentre x∈R tal que los vectores a = ⟨x, senx⟩  y  b = ⟨x, cosx⟩ sean equivalentes.

43. Calcule las coordenadas del punto D de manera que ABCD sea un paralelogramo, con A(1, 1), B(2, 4)  y  C(7, 4).

45. La rapidez de un objeto es la magnitud de su vector de velocidad relacionado. Una pelota de fútbol lanzada por un mariscal de campo tiene una velocidad inicial de 70 mph y un ángulo de elevación de 30°. Determine el vector de velocidad en mph y expréselo en forma de componentes. (Redondea a dos lugares decimales).

46. Un jugador de béisbol lanza una pelota de béisbol en un ángulo de 30° con la horizontal. Si la velocidad inicial de la pelota es de 100 mph, encuentre las componentes horizontal y vertical del vector de velocidad inicial de la pelota. (Redondea a dos lugares decimales).

47. Se dispara una bala con una velocidad inicial de 1500 pies/seg en un ángulo de 60° con la horizontal. Encuentra las componentes horizontal y vertical del vector de velocidad de la bala. (Redondea a dos lugares decimales).

48. [T] Un velocista de 65 kg ejerce una fuerza de 798 N en un ángulo de 19° con respecto al suelo en el taco de salida en el instante en que comienza una carrera. Encuentra el componente horizontal de la fuerza. (Redondea a dos lugares decimales).

49. [T] Dos fuerzas, una horizontal de 45 lb y otra de 52 lb, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de 25°. Encuentre la magnitud y el ángulo de dirección desde el eje x positivo de la fuerza resultante que actúa sobre el objeto. (Redondea a dos lugares decimales).

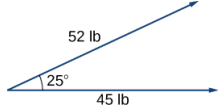
50. [T] Dos fuerzas, una fuerza vertical de 26 lb y otra de 45 lb, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de 55°. Encuentre la magnitud y el ángulo de dirección desde el eje x positivo de la fuerza resultante que actúa sobre el objeto. (Redondea a dos lugares decimales).

51. [T] Tres fuerzas actúan sobre el objeto. Dos de las fuerzas tienen las magnitudes 58 N y 27 N, y forman ángulos de 53° y 152°, respectivamente, con el eje x positivo. Encuentre la magnitud y el ángulo de dirección desde el eje x positivo de la tercera fuerza de manera que la fuerza resultante que actúa sobre el objeto sea cero. (Redondea a dos lugares decimales).

52. Tres fuerzas con magnitudes de 80 lb, 120 lb y 60 lb actúan sobre un objeto en ángulos de 45°, 60° y 30°, respectivamente, con el eje x positivo. Encuentre la magnitud y el ángulo de dirección desde el eje x positivo de la fuerza resultante. (Redondea a dos lugares decimales).

53. [T] Un avión vuela en la dirección de 43° al este del norte (también abreviado como N43E) a una velocidad de 550 mph. Un viento con velocidad de 25 mph viene del suroeste con un rumbo de N15E. ¿Cuáles son la velocidad respecto al suelo y la nueva dirección del avión?

54. [T] Un barco viaja en el agua a 30 mph en dirección N20E (es decir, 20° al este del norte). Una fuerte corriente se mueve a 15 mph en dirección N45E. ¿Cuáles son la nueva velocidad y dirección del barco?

55. [T] Un peso de 50 libras se cuelga de un cable de modo que las dos porciones del cable formen ángulos de 40° y 53°, respectivamente, con la horizontal. Encuentre las magnitudes de las fuerzas de tensión T₁ y T₂ en los cables si la fuerza resultante que actúa sobre el objeto es cero. (Redondea a dos lugares decimales).

56. [T] Un peso de 62 libras cuelga de una cuerda que forma los ángulos de 29° y 61°, respectivamente, con la horizontal. Encuentre las magnitudes de las fuerzas de tensión T₁ y T₂ en los cables si la fuerza resultante que actúa sobre el objeto es cero. (Redondea a dos lugares decimales).

57. [T] Un bote de 1500 lb está estacionado en una rampa que forma un ángulo de 30° con la horizontal. El vector de peso del barco apunta hacia abajo y es una suma de dos vectores: un vector horizontal v₁ que es paralelo a la rampa y un vector vertical v₂ que es perpendicular a la superficie inclinada. Las magnitudes de los vectores v₁ y v₂ son la componente horizontal y vertical, respectivamente, del vector de peso del barco. Encuentre las magnitudes de v₁ y v₂. (Redondea al número entero más cercano).

58. [T] Una caja de 85 libras está en reposo en una pendiente de 26°. Determine la magnitud de la fuerza paralela a la pendiente necesaria para evitar que la caja se deslice. (Redondea al número entero más cercano).

59. Un cable de sujeción sostiene un poste de 75 pies de altura. Un extremo del cable está unido a la parte superior del poste y el otro extremo está anclado al suelo a 50 pies de la base del poste. Determine las componentes horizontal y vertical de la fuerza de tensión en el alambre si su magnitud es de 50 lb (redondee al número entero más cercano).

60. El cable de sujeción de un poste telefónico tiene un ángulo de elevación de 35° con respecto al suelo. La fuerza de tensión en el cable de sujeción es de 120 lb. Encuentre las componentes horizontal y vertical de la fuerza de tensión. (Redondea al número entero más cercano).