Superficies cuadráticas

Superficies Cuadráticas

Hemos aprendido sobre superficies en tres dimensiones descritas por ecuaciones de primer grado; estos son planos. Algunos otros tipos comunes de superficies se pueden describir mediante ecuaciones de segundo grado. Podemos ver estas superficies como extensiones tridimensionales de las secciones cónicas que discutimos anteriormente: la elipse, la parábola y la hipérbola. Llamamos a estos gráficos superficies cuadráticas.

DEFINICIÓN. Superficies cuadráticas Las superficies cuadráticas son las gráficas de ecuaciones que se pueden expresar en la forma

Cuando una superficie cuadrática cruza con un plano de coordenadas, la traza es una sección cónica.

Un elipsoide es una superficie descrita por una ecuación de la forma

Establezca x = 0 para ver la traza del elipsoide en el plano yz. Para ver las trazas en los planos xy y xz, establezca z = 0 e y = 0, respectivamente. Observe que, si a = b, la traza en el plano xy es una circunferencia. De manera similar, si a = c, la traza en el plano xz es una circunferencia y, si b = c, entonces la traza en el plano yz es una circunferencia. Una esfera, entonces, es un elipsoide con a = b = c.

EJEMPLO ILUSTRATIVO 10.6_2. Dibujar un elipsoide

Dibuja el elipsoide

Solución:

Comience por dibujar los rastros. Para encontrar la traza en el plano xy, establezca z = 0:

Para encontrar los otros rastros, primero establezca y = 0 y luego establezca x = 0.

Ahora que sabemos cómo son las trazas de este sólido, podemos dibujar la superficie en tres dimensiones (Figura 10.6_8).

Figura 10.6_8 (a) Las trazas proporcionan un marco para la superficie. (b) El centro de este elipsoide es el origen.

La traza de un elipsoide es una elipse en cada uno de los planos de coordenadas. Sin embargo, este no tiene que ser el caso para todas las superficies cuadráticas. Muchas superficies cuadráticas tienen trazas que son diferentes tipos de secciones cónicas, y esto generalmente se indica con el nombre de la superficie. Por ejemplo, si una superficie puede describirse mediante una ecuación de la forma

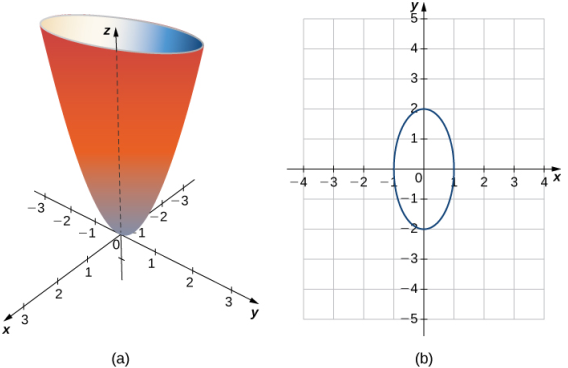
entonces llamamos a esa superficie un paraboloide elíptico. La traza en el plano xy es una elipse, pero las trazas en el plano xz y el plano yz son parábolas (Figura 10.6_9).

Otros paraboloides elípticos pueden tener otras orientaciones simplemente intercambiando las variables para darnos una variable diferente en el término lineal de la ecuación.

EJEMPLO ILUSTRATIVO 10.6_3. Identificación de rastros de superficies cuadráticas

Describir las trazas del paraboloide elíptico.

Solución:
Para encontrar la traza en el plano xy, establezca z = 0:

La traza en el plano z = 0 es simplemente un punto, el origen. Dado que un solo punto no nos dice cuál es la forma, podemos subir el eje z a un plano arbitrario para encontrar la forma de otros rastros de la figura.

La traza en el plano z = 5 es la gráfica de la ecuación

que es una elipse. En el plano xz, la ecuación se convierte en z = 5x^2. La traza es una parábola en este plano y en cualquier plano con la ecuación y = b.

En planos paralelos al plano yz, las trazas también son parábolas, como podemos ver en la siguiente figura.

Los hiperboloides de una hoja tienen algunas propiedades fascinantes. Por ejemplo, se pueden construir utilizando líneas rectas, como en la escultura de la Figura 10.6_11 (a). De hecho, las torres de enfriamiento para centrales nucleares a menudo se construyen en forma de hiperboloide. Los constructores pueden usar vigas de acero rectas en la construcción, lo que hace que las torres sean muy fuertes mientras usan relativamente poco material (Figura 106_11 (b)).

EJEMPLO ILUSTRATIVO 10.6_4. Encontrar el foco de un reflector parabólico

La energía que golpea la superficie de un reflector parabólico se concentra en el punto focal del reflector (Figura 10.6_12). Si la superficie de un reflector parabólico se describe por la ecuación

¿dónde está el punto focal del reflector?

Figura 10.6_12 La energía se refleja en el reflector parabólico y se recoge en el punto focal. (crédito: modificación de CGP Gray, Wikimedia Commons)

Solución:
Como z es la variable de primera potencia, el eje del reflector corresponde al eje z. Los coeficientes de x² e y² son iguales, por lo que la sección transversal del paraboloide perpendicular al eje z es una circunferencia. Podemos considerar una traza en el plano xz o en el plano yz; el resultado es el mismo. Estableciendo y = 0, la traza es una parábola que se abre a lo largo del eje z, con la ecuación estándar x² = 4pz, donde p es la distancia focal de la parábola. En este caso, esta ecuación se convierte en x² = 100⋅z/4 = 4pz o 25 = 4p. Entonces p es 6.25 m, lo que nos dice que el foco del paraboloide está 6.25 m arriba del eje desde el vértice. Debido a que el vértice de esta superficie es el origen, el punto focal es (0, 0, 6.25).

Diecisiete superficies cuadráticas estándar pueden derivarse de la ecuación general

Las siguientes figuras resumen las más importantes.

Características comunes de las superficies cuadráticas

(Figura 10.6_13 Características de las superficies cuadráticas comunes: elipsoide, hiperboloide de una hoja, hiperboloide de dos hojas.)

Características comunes de las superficies cuadráticas

(Figura 106_14 Características de las superficies cuadráticas comunes: cono elíptico, paraboloide elíptico, paraboloide hiperbólico.)

EJEMPLO ILUSTRATIVO 10.6_5. Identificación de ecuaciones de superficies cuadráticas

Identifica las superficies representadas por las ecuaciones dadas.

Solución:
a. Los términos x, y y z son todos al cuadrado, y todos son positivos, por lo que este es probablemente un elipsoide. Sin embargo, vamos a poner la ecuación en la forma estándar para un elipsoide solo para estar seguros. Tenemos

Dividiendo todos los términos por 144, se obtiene

Entonces, esto es, de hecho, un elipsoide, centrado en el origen.

b. Primero notamos que el término z se eleva sólo a la primera potencia, por lo que este es un paraboloide elíptico o un paraboloide hiperbólico. También notamos que hay términos xy términos y que no son cuadrados, por lo que esta superficie cuadrática no está centrada en el origen. Necesitamos completar el cuadrado para poner esta ecuación en una de las formas estándar. Tenemos

Este es un paraboloide elíptico centrado en (1, 2, 0).