Solución de problemas de optimización cuando el intervalo no está cerrado o no está limitado
En los ejemplos anteriores, consideramos funciones en dominios cerrados y acotados. En consecuencia, por el teorema del valor extremo, se nos garantizó que las funciones tenían extremos absolutos. Consideremos ahora las funciones para las cuales el dominio no está cerrado ni limitado.
Muchas funciones todavía tienen al menos un extremo absoluto, incluso si el dominio no está cerrado o el dominio no tiene límites. Por ejemplo, la función f (x) = x2 + 4 sobre (−∞, ∞) tiene un mínimo absoluto de 4 en x = 0. Por lo tanto, aún podemos considerar funciones sobre dominios ilimitados o intervalos abiertos y determinar si tienen algún extremo absoluto. En el siguiente ejemplo, tratamos de minimizar una función sobre un dominio ilimitado. Veremos que, aunque el dominio de consideración es (0, ∞), la función tiene un mínimo absoluto. En la solución del problema ilustrativo que sigue, observamos la construcción de una caja de menor superficie con un volumen prescrito. No es difícil demostrar que, para una caja superior cerrada, por simetría, entre todas las cajas con un volumen especificado, un cubo tendrá el área de superficie más pequeña. En consecuencia, consideramos el problema modificado de determinar qué caja abierta con un volumen especificado tiene el área de superficie más pequeña.
Minimizando un área de superficie
Se construirá una caja rectangular con una base cuadrada, una parte superior abierta y un volumen de 216 pulgadas. ¿Cuáles deberían ser las dimensiones de la caja para minimizar el área de superficie de la caja? ¿Cuál es el área de superficie mínima?
Solución:
Paso 1: Se dibuja una caja rectangular e introduce la variable x para representar la longitud de cada lado de la base cuadrada, en pulgadas; la letra y representa la altura de la caja, en plg. La letra S denota el área de superficie del cuadrado superior abierto, en pulgadas cuadradas.


Paso 2: Necesitamos minimizar el área de la superficie. Por lo tanto, debemos minimizar S.
Paso 3: Dado que la caja tiene una parte superior abierta, solo necesitamos determinar el área de los cuatro lados verticales y la base cuadrada. El área de cada uno de los cuatro lados verticales es x⋅y. El área de la base es x2. Por lo tanto, el área de la superficie de la caja es
S = 4xy + x2.
Paso 4: Dado que el volumen de esta caja es x2 y y el volumen que se da es 216 plg.3, la ecuación de restricción es
x2 y = 216.
Resolviendo la ecuación de restricción para y, tenemos y = 216/x2. Por lo tanto, podemos escribir el área de la superficie en función de la variable independiente x solamente:
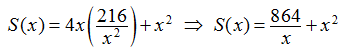
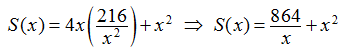
Paso 5: Dado que estamos requiriendo que x2y = 216, no podemos tener x = 0. Por lo tanto, necesitamos x > 0. Por otro lado, x puede tener cualquier valor positivo. Tenga en cuenta que a medida que x se hace grande, la altura y de la caja se hace correspondientemente pequeña, de modo que se cumpla x2y = 216. Del mismo modo, a medida que x se vuelve pequeña, la altura de la caja se vuelve correspondientemente grande. Llegamos a la conclusión de que el dominio es el intervalo abierto, sin límites (0, ∞). Tenga en cuenta que, a diferencia de los ejemplos anteriores, no podemos reducir nuestro problema a buscar un máximo absoluto o un mínimo absoluto en un intervalo cerrado y acotado. Sin embargo, en el siguiente paso, descubrimos por qué esta función debe tener un mínimo absoluto durante el intervalo (0, ∞).
Paso 6: Tenga en cuenta que cuando x → 0+, S (x) → ∞. Además, cuando x → ∞, S (x) → ∞. Como S es una función continua que se aproxima al infinito en los extremos, debe tener un mínimo absoluto en algún x ∈ (0, ∞). Este mínimo debe ocurrir en un punto crítico de S. La derivada de S es
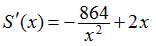
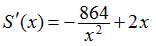
Por lo tanto, S‘ (x) = 0 cuando 2x = 864 / x2. Al resolver esta ecuación para x, obtenemos x3 = 432, entonces
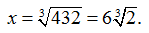
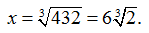
Como este es el único punto crítico de S, el mínimo absoluto debe ocurrir allí (ver Figura 4.38). Cuando


Por lo tanto, las dimensiones de la caja deben ser
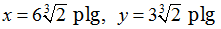
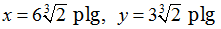
Con estas dimensiones, el área de la superficie de la caja es




Figura 4.38 Podemos usar la gráfica de S para determinar las dimensiones de la caja y el área de superficie mínima dado el volumen.

¡Hurra! Por fin encontré una página web desde donde soy capaz de obtener genuinamente datos útiles sobre mi estudio y así obtener más conocimiento.