Otras estrategias para la integración: Objetivos de aprendizaje
5.12.1. Use una tabla de integrales para resolver problemas de integración.
5.12.2. Use un sistema de álgebra computacional (CAS) para resolver problemas de integración.
Además de las técnicas de integración que ya hemos visto, hay muchas otras herramientas disponibles para ayudar con el proceso de integración. Entre estas herramientas están las tablas de integración, que están fácilmente disponibles en muchos libros, incluidos los apéndices de este. También están ampliamente disponibles los sistemas de álgebra computacional (CAS), que se encuentran en las calculadoras y en muchos laboratorios de computación del campus, y son gratuitos en línea.
Tablas de integrales
Las tablas de integración, si se usan de la manera correcta, pueden ser una forma práctica de evaluar o verificar una integral rápidamente. Tenga en cuenta que cuando usa una tabla para verificar una respuesta, es posible que dos soluciones completamente correctas se vean muy diferentes. Por ejemplo, en la Sustitución trigonométrica, encontramos que, al usar la sustitución x = tanθ, podemos llegar a
Sin embargo, usando x = senhθ, obtuvimos una solución diferente, a saber,
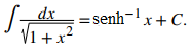
Más tarde demostramos algebraicamente que las dos soluciones son equivalentes. Es decir, demostramos que
En este caso, los dos antiderivadas que encontramos fueron en realidad iguales. Este no tiene por qué ser el caso. Sin embargo, mientras la diferencia en los dos antiderivadas sea constante, son equivalentes.
Ejemplo ilustrativo 5.12_1 Usar una fórmula de una tabla para evaluar una integral
Usa la siguiente fórmula, dada en la tabla de integrales
para evaluar
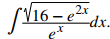
Solución:
Si miramos las tablas de integración, vemos que varias fórmulas contienen expresiones de la forma √(a² − u²). Esta expresión es en realidad similar a √(16 – e²˟), donde a = 4 y u = e˟. Tenga en cuenta que también debemos tener du = e˟ dx. Multiplicar el numerador y el denominador de la integral dada por e˟ debería ayudar a poner esta integral en una forma útil. Por lo tanto, ahora tenemos
Sustituyendo u = e˟ y du = e˟ dx produce
De la tabla de integración (# 88 en el Apéndice A),
De tal modo que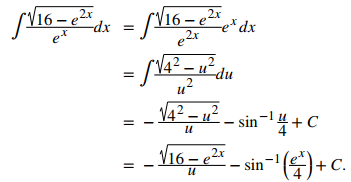
◊
Sistemas de álgebra computacional
Si está disponible, un CAS es una alternativa más rápida a una tabla para resolver un problema de integración. Muchos de estos sistemas están ampliamente disponibles y, en general, son bastante fáciles de usar.
Ejemplo ilustrativo 5.12_2 Uso de un sistema informático de álgebra para evaluar una integral
Use un sistema de álgebra computacional para evaluar
Compare este resultado con
un resultado que podríamos haber obtenido si hubiéramos usado la sustitución trigonométrica.
Solución:
Usando Wolfram Alpha, obtenemos
Tenga presente que
Dado que estas dos antiderivadas difieren solo por una constante, las soluciones son equivalentes. También podríamos haber demostrado que cada uno de estas antiderivadas es correcta por derivación. ◊
Ejemplo ilustrativo 5.12_3 Usando un CAS para evaluar una integral
Evalúe ∫sen³xdx usando un CAS. Compare el resultado con (1/3)cos³x − cosx + C, el resultado que podríamos haber obtenido utilizando la técnica para integrar potencias impares de senx discutidos anteriormente en este capítulo.
Solución:
Usando Wolfram Alpha, obtenemos
Esto se ve bastante diferente de (1/3)cos³x − cosx + C. Para ver que estas antiderivadas son equivalentes, podemos utilizar algunas identidades trigonométricas:
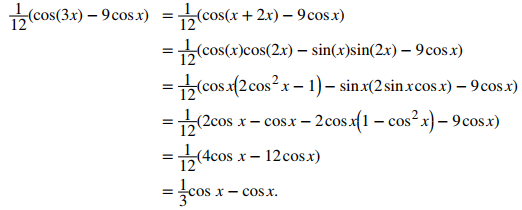
Por lo tanto, las dos antiderivadas son idénticas.
También podemos usar un CAS para comparar las gráficas de las dos funciones, como se muestra en la siguiente figura.
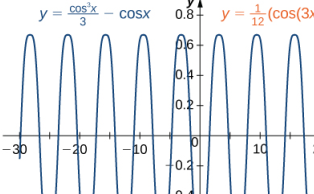
(Figura 5.12_1 Las gráficas de y = (1/3)cos³x − cosx e y = (1/12) (cos(3x) −9cosx) son idénticas.) ◊