Cambio poblacional
Además de analizar la velocidad, la rapidez, la aceleración y la posición, podemos usar derivados para analizar varios tipos de poblaciones, incluidas aquellas tan diversas como las colonias de bacterias y las ciudades. Podemos usar una población actual, junto con una tasa de crecimiento, para estimar el tamaño de una población en el futuro. La tasa de crecimiento de la población es la tasa de cambio de una población y, en consecuencia, puede representarse por la derivada del tamaño de la población.
DEFINICIÓN. Tasa de crecimiento de una población
| Si P(t) es el número de individuos presentes en una población, entonces la tasa de crecimiento de la población P(t) se define como P′(t). |
Ejemplo ilustrativo 3.4_5. Estimando una Población
La población de una ciudad se triplica cada 5 años. Si su población actual es de 10,000, ¿cuál será su población aproximada dentro de 2 años?
Solución:
Sea P(t) la población (en miles) t años a partir de ahora. Por lo tanto, sabemos que P(0) = 10 y en base a la información, anticipamos P(5) = 30. Ahora se estima P′(0), la tasa de crecimiento actual, usando


Al aplicar la fórmula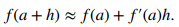
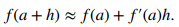


así, en 2 años la población será de, aproximadamente, 18,000 individuos. ◊
Cambios en costos e ingresos
Además de analizar el movimiento a lo largo de una recta y el crecimiento de la población, las derivadas son útiles para analizar los cambios en el costo, los ingresos y las ganancias. El concepto de una función marginal es común en los campos de los negocios y la economía e implica el uso de derivadas. El costo marginal es la derivada de la función de costo. El ingreso marginal es la derivada de la función de ingreso. La utilidad marginal es la derivada de la función de utilidad, que se basa en la función de costo y la función de ingresos.
DEFINICIÓN. Costo marginal, ingreso marginal y utilidad marginal
|
Podemos obtener una aproximación de


eligiendo un valor apropiado para h. Como x representa objetos, un valor razonable y pequeño para h es 1. Por lo tanto, al sustituir h = 1, obtenemos la aproximación MC(x) = C(x) ≈ C′(x + 1) − C(x). En consecuencia, C′(x) para un valor dado de x puede considerarse como el cambio en el costo asociado con la producción de un artículo adicional. De manera similar, MR(x) = R′(x) se aproxima a los ingresos obtenidos por la venta de un artículo adicional, y MP(x) = P′(x) se aproxima a la ganancia obtenida al producir y vender un artículo adicional.
Ejemplo ilustrativo 3.4_6. Aplicando ingresos marginales
Suponga que el número de cenas de barbacoa, x, que se pueden vender está relacionado con el precio cobrado, p, por la ecuación p(x) = 9 − 0.03x, 0 ≤ x ≤ 300.
En este caso, los ingresos en dólares obtenidos al vender x cenas de barbacoa están dados por
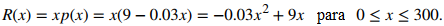
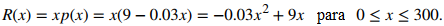
Use la función de ingresos marginales para estimar los ingresos obtenidos de la venta de la 101-ava cena de barbacoa. Compare esto con los ingresos reales obtenidos de la venta de esta cena.
Solución:
Primero, encuentre la función de ingreso marginal: MR(x) = R′(x) = – 0.06x + 9.
Luego, use R′(100) para aproximar R(101) − R(100), los ingresos obtenidos de la venta de la 10.ava cena. Dado que R′(100) = 3, los ingresos obtenidos de la venta de la cena número 101 son de aproximadamente $3.
Los ingresos reales obtenidos de la venta de la 101ª cena son


El ingreso marginal es una estimación bastante buena en este caso y tiene la ventaja de ser fácil de calcular.

El contenido de calidad es la clave para atraer a las personas a visitar un sitio web, eso es lo que ofrece este sitio web, me encanta la matemática bien explicada!.