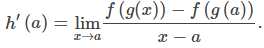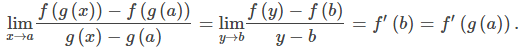Combinando la regla de la cadena con otras reglas
Ahora que podemos combinar la regla de la cadena y la regla de la potencia, examinamos cómo combinar la regla de la cadena con las otras reglas que hemos aprendido. En particular, podemos usarlo con las fórmulas para las derivadas de funciones trigonométricas o con la regla del producto.
Ejemplo ilustrativo 3.6_4. Uso de la regla de la cadena en una función coseno general
Encuentre la derivada de h(x) = cos(g(x)).
Solución:
Piense en h(x) = cos(g(x)) como f (g(x)) donde f (x) = cosx. Como f ′(x) = – senx. tenemos f ′(g(x)) = – sen(g(x). Luego hacemos el siguiente cálculo.
Por lo tanto, la derivada de h(x) = cos(g(x)) viene dada por h′(x) = – sen(g(x)) g′(x). ◊
En el siguiente ejemplo aplicamos la regla que acabamos de deducir.
Ejemplo ilustrativo 3.6_5. Usando la regla de la cadena en una función coseno
Encuentre la derivada de h(x) = cos(5x²).
Solución:
Sea g(x) = 5x². Entonces g ′(x) = 10x. Usando el resultado del ejemplo anterior,
◊
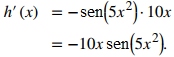
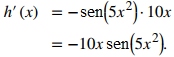
Ejemplo ilustrativo 3.6_6. Uso de la regla de la cadena en una función trigonométrica
Encuentre la derivada de h(x) = sec(4x⁵ + 2x).
Solución:
Aplique la regla de la cadena a h(x) = sec(g(x)) para obtener
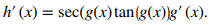
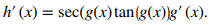
En este problema, g(x) = 4x⁵ + 2x, entonces tenemos g′(x) = 20x⁴ + 2. Por lo tanto, obtenemos
◊
En este punto, proporcionamos una lista de fórmulas de derivadas que se pueden obtener aplicando la regla de la cadena junto con las fórmulas para derivadas de funciones trigonométricas. Sus deducciones son similares a las utilizadas en el ejemplo 3.6_4 y el ejemplo 3.6_6. Por conveniencia, las fórmulas también se dan en la notación de Leibniz, que algunos estudiantes encuentran más fácil de recordar. (Discutimos la regla de la cadena usando la notación de Leibniz al final de esta sección). No es absolutamente necesario memorizarlos como fórmulas separadas, ya que todas son aplicaciones de la regla de la cadena a fórmulas aprendidas previamente.
TEOREMA 3.6.1. Usando la regla de la cadena con funciones trigonométricas
|
Para todos los valores de x para los que se define la derivada,
|
Ejemplo ilustrativo 3.6_7. Combinando la regla de la cadena con la regla del producto
Encuentre la derivada de h(x) = (2x + 1)⁵ (3x − 2)⁷.
Solución:
Primero aplique la regla del producto, luego aplique la regla de la cadena a cada término del producto.
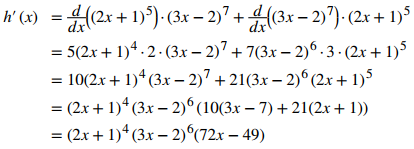
Composición de tres o más funciones
Ahora podemos combinar la regla de la cadena con otras reglas para diferenciar las funciones, pero cuando estamos diferenciando la composición de tres o más funciones, necesitamos aplicar la regla de la cadena más de una vez. Si observamos esta situación en términos generales, podemos generar una fórmula, pero no necesitamos recordarla, ya que simplemente podemos aplicar la regla de la cadena varias veces.
En términos generales, primero dejamos
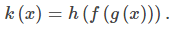
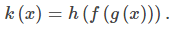
Luego, aplicando la regla de la cadena una vez que obtenemos
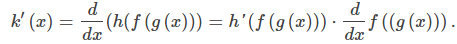
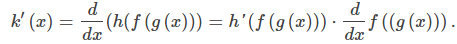
Aplicando nuevamente la regla de la cadena, obtenemos
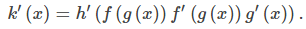
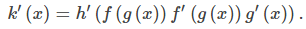
REGLA 3.6_3: REGLA DE CADENA PARA UNA COMPOSICIÓN DE TRES FUNCIONES
|
Para todos los valores de x para los que la función es diferenciable, si
entonces
En otras palabras, estamos aplicando la regla de la cadena dos veces. |
Observe que la derivada de la composición de tres funciones tiene tres partes. (Del mismo modo, la derivada de la composición de cuatro funciones tiene cuatro partes, etc.) Además, recuerde, siempre podemos trabajar desde afuera hacia adentro, tomando una derivada a la vez.
Ejemplo ilustrativo 3.6_8. Diferenciando una composición de tres funciones
Encuentre la derivada de k(x) = cos⁴(7x² + 1).
Solución:
Primero, reescribe k(x) como
Luego aplique la regla de la cadena varias veces.
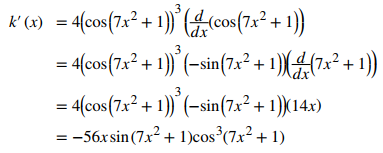
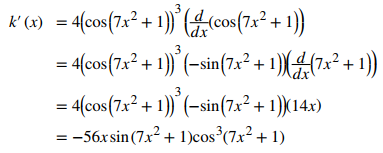
Ejemplo ilustrativo 3.6_9. Usando la regla de la cadena en un problema de velocidad
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo t viene dada por s(t) = sin (2t) + cos (3t). ¿Cuál es la velocidad de la partícula en el tiempo t = π/6?
Solución:
Para encontrar v(t), la velocidad de la partícula en el tiempo t, debemos diferenciar s(t). Así,
Sustituyendo t = π/6 en v(t), obtenemos v(π/6) = – 2. ◊
Prueba informal de la regla de la cadenaEn este punto, presentamos una prueba muy informal de la regla de la cadena. Por simplicidad, ignoramos ciertos problemas: por ejemplo, suponemos que g(x) ≠ g(a) para x ≠ a en un intervalo abierto que contiene a a. Comenzamos aplicando la definición de límite de la derivada a la función h(x) para obtener h′(a):
|
Reescribiendo, obtenemos
Aunque está claro que
Para ver que esto es cierto, primero recuerde que dado que g es diferenciable en a, g también es continua en a. Así,
A continuación, realice la sustitución y = g(x) y b = g(a) y utilice el cambio de variables en el límite para obtener
Finalmente,
◊Ejemplo ilustrativo 3.6_10. Usando la regla de la cadena con valores funcionales
Sea h(x) = f (g(x)). Si g(1) = 4, g′(1) = 3 y f ′(4) = 7, encuentre h′(1).
Solución:
Use la regla de la cadena, luego sustitúyase
◊
La regla de la cadena usando la notación de Leibniz
Al igual que con otras derivadas que hemos visto, podemos expresar la regla de la cadena utilizando la notación de Leibniz. Esta notación para la regla de la cadena se usa mucho en aplicaciones de física.
Para h(x) = f (g(x)), sea u = g(x) e y = h(x) = f (u). Se tiene que,
Por consiguiente,
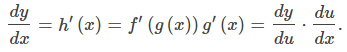
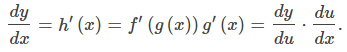
REGLA 3.6_4: REGLA DE CADENA CON LA NOTACIÓN DE LEIBNIZ
|
Si y es una función de u, y u es una función de x, entonces
|
Ejemplo ilustrativo 3.6_11. Tomar una derivada usando la notación de Leibniz, ejemplo 1
Encuentre la derivada de y = (x/(3x + 2))⁵.
Solución:
Primero, sea u = x/(3x + 2). Por lo tanto, y = u⁵. Luego, encuentra du/dx y dy/du. Usando la regla del cociente,
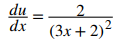
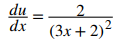
y
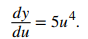
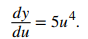
Finalmente, lo juntamos todo.
Es importante recordar que, cuando se usa la forma de Leibniz de la regla de la cadena, la respuesta final debe expresarse completamente en términos de la variable original dada en el problema. ◊
Ejemplo ilustrativo 3.6_12. Tomar una derivada usando la notación de Leibniz, ejemplo 2
Encuentre la derivada de y = tan(4x² − 3x + 1).
Solución:
Primero, sea u = 4x² − 3x + 1. Entonces y = tanu. A continuación, encuentre du/dx y dy/du:
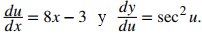
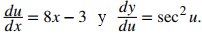
Finalmente, lo juntamos todo.
◊