La serie p
La serie armónica
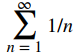
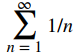
y la serie
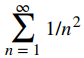
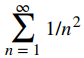
son ejemplos de un tipo de serie llamada serie p.
DEFINICIÓN 7.3_1. Serie p
|
Para cualquier número real p, la serie
se llama serie p. |
Sabemos que la serie p converge si p = 2 y diverge si p = 1. ¿Qué pasa con otros valores de p? En general, es difícil, si no imposible, calcular el valor exacto de la mayoría de las series p. Sin embargo, podemos usar las pruebas presentadas hasta ahora para probar si una serie p converge o diverge.
Si p < 0, entonces 1/nᴾ → ∞, y si p = 0, entonces 1/nᴾ → 1. Por lo tanto, por la prueba de divergencia,
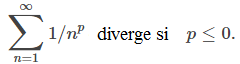
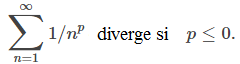
Si p > 0, entonces f (x) = 1/xᴾ es una función positiva, continua y decreciente. Por lo tanto, para p > 0, usamos la prueba integral, comparando
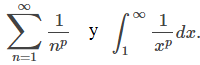
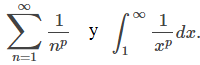
Ya hemos considerado el caso cuando p = 1. Aquí consideramos el caso cuando p > 0, p ≠ 1. Para este caso,
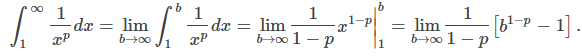
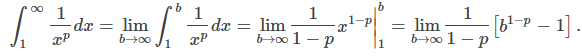
Porque
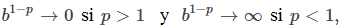
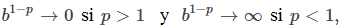
concluimos que
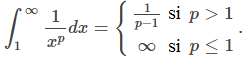
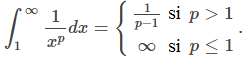
Por lo tanto,


converge si p > 1 y diverge si 0 < p < 1.
En resumen,


EJEMPLO ILUSTRATIVO 7.3_3. Prueba de convergencia de la serie p
Para cada una de las siguientes series, determine si converge o diverge.
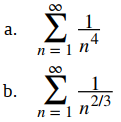
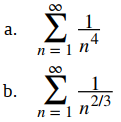
Solución:
a. Esta es una serie p con p = 4 > 1, por lo que la serie converge.
b. Como p = 2/3 < 1, la serie diverge.
Estimando el valor de una serie
Supongamos que sabemos que una serie
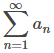
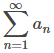
converge y queremos estimar la suma de esa serie. Ciertamente podemos aproximar esa suma usando cualquier suma finita
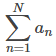
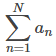
donde N es cualquier número entero positivo. La pregunta que abordamos aquí es, para una serie convergente
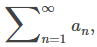
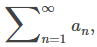
que tan buena es la aproximación
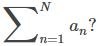
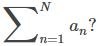
Más específicamente, si dejamos que
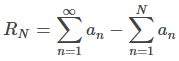
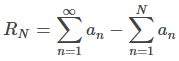
sea el resto cuando la suma de una serie infinita se aproxima por la enésima suma parcial, ¿qué tan grande es RN? Para algunos tipos de series, podemos usar las ideas de la prueba integral para estimar RN.
TEOREMA 7.3_2. Estimación del remanente en la prueba de la integral
|
Supongamos que i. f es continua, Deje que SN sea la enésima suma parcial de Para todos los enteros positivos N,
En otras palabras, el resto o remanente
satisface la siguiente estimación:
Esto se conoce como la estimación remanente. |
Ilustramos la estimación remanente en la prueba de la integral en la figura 7.3_4. En particular, al representar el resto RN = aN + 1 + aN + 2 + aN + 3 + ⋯ como la suma de las áreas de los rectángulos, vemos que el área de esos rectángulos está limitada por
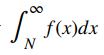
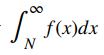
y acotado abajo por
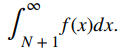
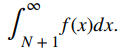
En otras palabras,
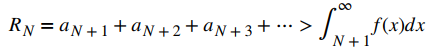
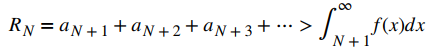
y
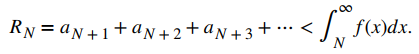
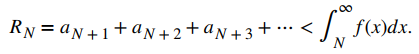
Concluimos que
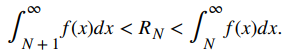
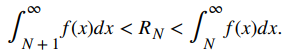
Ya que


donde SN es la enésima suma parcial, concluimos que


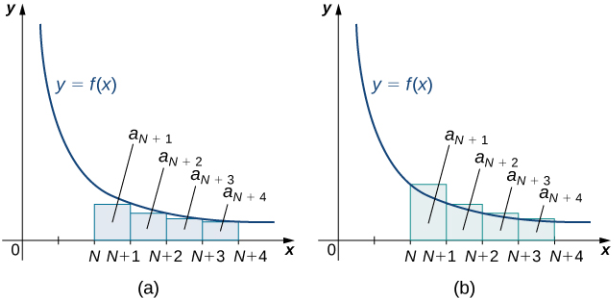

Figura 7.3_4 Dada una función continua, positiva y decreciente f, y una secuencia de términos positivos an tal que an = f (n) para todos los enteros positivos n,
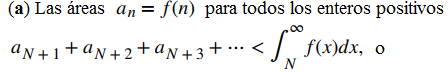
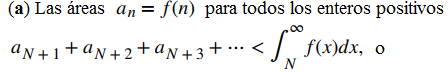
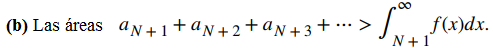
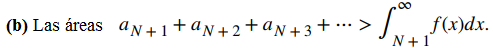
Por lo tanto, la integral es una sobreestimación o una subestimación del error.
EJEMPLO ILUSTRATIVO 7.3_4. Estimando el valor de una serie
Considere la serie
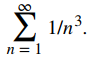
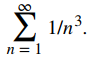
a. Calcule


y estime el error.
b. Determine el menor valor de N necesario de modo que SN estimará
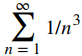
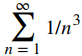
hasta dentro de 0.001.
Solución:
a. Usando una calculadora, obtenemos
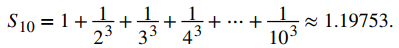
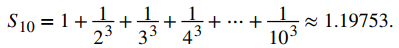
Según la estimación remanente, sabemos que
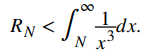
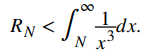
Tenemos que
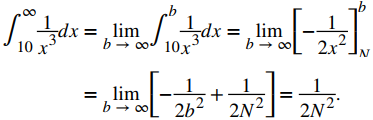
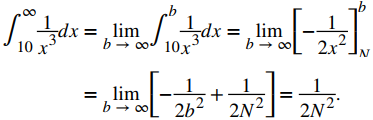
Por lo tanto, el error es R10 <1/2(10)² = 0.005.
b. Encuentre N tal que RN < 0.001. En la parte a. mostramos que RN < 1 / 2N². Por lo tanto, el resto RN <0.001 siempre que 1/2N² < 0.001. Es decir, necesitamos 2N² > 1000. Al resolver esta desigualdad para N, vemos que necesitamos N > 22.36. Para garantizar que el resto esté dentro de la cantidad deseada, debemos redondear al entero más cercano. Por lo tanto, el valor mínimo necesario es N = 23.




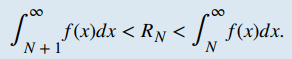
Explicación muy clara y completa. Excelente la resolción de ejemplos pertinentes.