Integrales que implican funciones exponenciales y logarítmicas

Integrales que implican funciones logarítmicas

Las funciones integradas de la forma f (x) = x‾¹ dan como resultado el valor absoluto de la función logaritmo natural, como se muestra en la siguiente regla. Las fórmulas integrales para otras funciones logarítmicas, como f (x) = lnx y f (x) = log_ax, también se incluyen en la regla.

REGLA 5.6.2: FÓRMULAS DE INTEGRACIÓN QUE INCLUYEN FUNCIONES LOGARÍTMICAS

Las siguientes fórmulas se pueden usar para evaluar integrales que involucran funciones logarítmicas:

EJEMPLO ILUSTRATIVO 5.6_10. Encontrar una antiderivada que involucra lnx

Encuentre la antiderivada de la función 3/(x − 10).

Solución:
Primero factoriza el 3 fuera del símbolo integral. Luego usa la regla u‾¹. Así,

EJEMPLO ILUSTRATIVO 5.6_11. Encontrar una antiderivada de una función racional

Encuentra la antiderivada deLa función a integrar puede reescribirse como

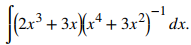
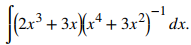
Usar sustitución u. Sea u = x⁴ + 3x², luego du = 4x³ + 6x. Cambiamos du factorizando por 2. Por lo tanto,

Reescribe el integrando en términos de u:

Entonces obtenemos

◊

EJEMPLO ILUSTRATIVO 5.6_12. Encontrar la antiderivada de una función logarítmica

Encuentre la antiderivada de la función logarítmica log₂x.

Solución:
Siga el formato en la fórmula que figura en la regla sobre fórmulas de integración que involucran funciones logarítmicas. En base a este formato, tenemos◊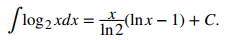

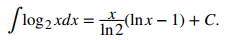
En el ejemplo 5.6_13 se tiene una integral definida de una función trigonométrica. Con las funciones trigonométricas, a menudo tenemos que aplicar una propiedad trigonométrica o una identidad antes de poder avanzar. Encontrar la forma correcta del integrando suele ser la clave para una integración fluida.

EJEMPLO ILUSTRATIVO 5.6_13. Evaluación de una integral definida

Encuentra la integral definida de

Solución:
Necesitamos sustitución u para resolver este problema. Sea u = 1 + cosx, entonces du = −senxdx. Reescribe la integral en términos de u, cambiando también los límites de integración. Así,

Entonces,

◊