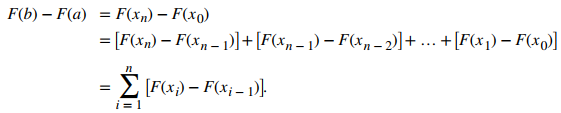Teorema fundamental del cálculo, Parte 2: El teorema de la evaluación

El teorema fundamental del cálculo, Parte 2, es quizás el teorema más importante en el cálculo. Después de los incansables esfuerzos de los matemáticos durante aproximadamente 500 años, surgieron nuevas técnicas que proporcionaron a los científicos las herramientas necesarias para explicar muchos fenómenos. Utilizando el cálculo, los astrónomos finalmente podrían determinar distancias en el espacio y mapear órbitas planetarias. Los problemas financieros cotidianos, como el cálculo de los costos marginales o la predicción de las ganancias totales, ahora se pueden manejar con simplicidad y precisión. Los ingenieros pueden calcular la resistencia a la flexión de los materiales o el movimiento tridimensional de los objetos. Nuestra visión del mundo cambió para siempre con el cálculo.

Después de encontrar áreas aproximadas al sumar las áreas de n rectángulos, la aplicación de este teorema es sencilla en comparación. Casi parece demasiado simple que el área de una región curva completa se pueda calcular simplemente evaluando una antiderivada en el primer y último punto final de un intervalo.

TEOREMA 5.3.3. Teorema fundamental del cálculo Parte 2

Si f es continua en el intervalo [a, b] y F(x) es cualquier antiderivada de f (x), entonces

A menudo vemos la notación

para denotar la expresión F(b) − F(a). Utilizamos esta barra vertical y los límites asociados a y b para indicar que debemos evaluar la función F(x) en el límite superior (en este caso, b), y restar el valor de la función F(x) evaluada en el límite inferior (en este caso, a).

El teorema fundamental del cálculo, Parte 2 (también conocido como teorema de evaluación) establece que si podemos encontrar una antiderivada para el integrando, entonces podemos evaluar la integral definida evaluando la antiderivada en los puntos finales del intervalo y restando.

Prueba Sea P = {xᵢ}, i = 0, 1, …, n una partición regular de [a, b]. Entonces, podemos escribirAhora, sabemos que F es una antiderivada de f sobre [a, b], así que por el Teorema del valor medio (ver El teorema del valor medio) para i = 0, 1, …, n podemos encontrar cᵢ en [xᵢ₋₁, xᵢ] tal queLuego, sustituyendo en la ecuación anterior, tenemosTomando el límite de ambos lados cuando n → ∞, obtenemos□

EJEMPLO ILUSTRATIVO 5.3_6. Evaluación de una integral con el teorema fundamental del cálculo

Utilice el teorema fundamental del cálculo, parte 2 para evaluar

Solución:
Recordemos la regla de la potencia para las antiderivadas:

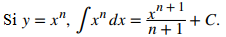
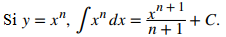
Use esta regla para encontrar la antiderivada de la función y luego aplique el teorema. Tenemos

Análisis

Tenga en cuenta que no incluimos el término “+ C” cuando escribimos la antiderivada. La razón es que, de acuerdo con el Teorema fundamental del cálculo, Parte 2, cualquiera sirve como antiderivada. Entonces, por conveniencia, elegimos la antiderivada con C = 0. Si hubiéramos elegido otro antiderivada, para cualquier otro valor de C distinto de 0, el término constante se habría cancelado. Esto siempre sucede al evaluar una integral definida.

La región del área que acabamos de calcular se representa en la figura 5.3_3. Tenga en cuenta que la región entre la curva y el eje x está debajo del eje x. El área siempre es positiva, pero una integral definida aún puede producir un número negativo (un área neta con signo). Por ejemplo, si esta fuera una función de ganancias, un número negativo indica que la compañía está operando con pérdidas durante el intervalo dado.

Figura 5.3_3 La evaluación de una integral definida puede producir un valor negativo, aunque el área siempre es positiva. ◊

EJEMPLO ILUSTRATIVO 5.3_7. Evaluación de una integral definida utilizando el teorema fundamental del cálculo,  parte 2

Evalúe la siguiente integral utilizando el Teorema fundamental del cálculo, Parte 2:

Solución:

Primero, elimine el radical reescribiendo la integral usando exponentes racionales. Luego, separe los términos del numerador escribiendo cada uno sobre el denominador:

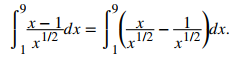
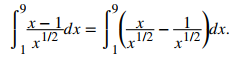
Usa las propiedades de los exponentes para simplificar:

Ahora, integre usando la regla de la potencia:

Figura 5.3_4 El área bajo la curva de x = 1 a x = 9 se puede calcular evaluando una integral definida. ◊

EJEMPLO ILUSTRATIVO 5.3_8. Una carrera de patinaje

James y Kathy corren en patines. Corren a lo largo de una pista larga y recta, y quien haya llegado más lejos después de 5 segundos gana un premio. Si James puede patinar a una velocidad de f (t) = 5 + 2t pies/seg y Kathy puede patinar a una velocidad de g(t) = 10 + cos (πt/2) pies/seg, ¿quién ganará la carrera?

Solución:
Necesitamos integrar ambas funciones durante el intervalo [0, 5] y ver qué valor es mayor. Para James, queremos calcular

Usando la regla de la potencia, tenemos

Por lo tanto, James ha patinado 50 pies después de 5 segundos. Volviendo ahora a Kathy, queremos calcular

Sabemos que sent es una antiderivada de cost, por lo que es razonable esperar que una antiderivada de cos(πt/2) implique sen(πt/2). Sin embargo, cuando diferenciamos sen(πt/2), obtenemos (π/2)cos(πt/2) como resultado de la regla de la cadena, por lo que tenemos que tener en cuenta este coeficiente adicional cuando integramos. Obtenemos

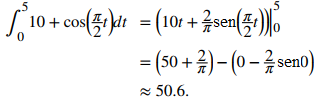
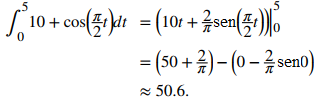
Kathy ha patinado aproximadamente 50.6 pies después de 5 segundos. ¡Kathy gana, pero no por mucho!  ◊