ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
Ejercicios propuestos del Capítulo 8.1
Para los siguientes ejercicios, dibuje las curvas correspondientes eliminando el parámetro t. De la orientación de la curva.
1. x = t² + 2t, y = t + 1
2. x = cos(t), y = sen(t), (0, 2π]
3. x = 2t + 4, y = t − 1
4. x = 3 − t, y = 2t − 3, 1.5 ≤ t ≤ 3
Para e siguiente ejercicio, elimine el parámetro y dibuje la gráfica correspondiente.
5. x = 2t², y = t⁴ + 1
Para los siguientes ejercicios, use tecnología (CAS o calculadora) para bosquejar las ecuaciones paramétricas.
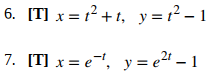
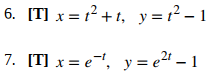
8. [T] x = 3cost, y = 4sent
9. [T] x = sect, y = cost
Para los siguientes ejercicios, dibuje las ecuaciones paramétricas eliminando el parámetro. Indique las asíntotas del gráfico.

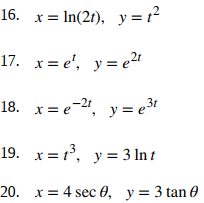
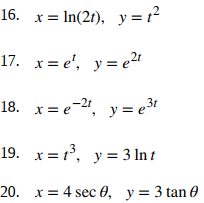
Para los siguientes ejercicios, convierta las ecuaciones paramétricas de una curva en forma rectangular. No es necesario un boceto. Indique el dominio de la forma rectangular.
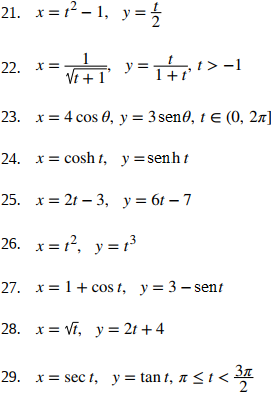
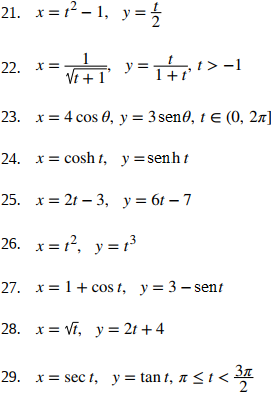


Para los siguientes ejercicios, los pares de ecuaciones paramétricas representan rectas, parábolas, circunferencias, elipses o hipérbolas. Nombra el tipo de curva básica que representa cada par de ecuaciones.
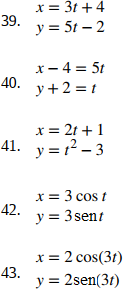
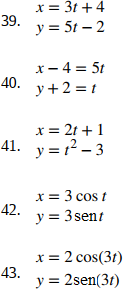
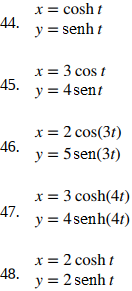
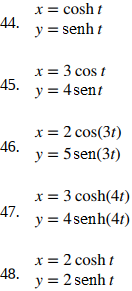
49. Demuestre que
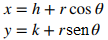
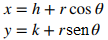
representa la ecuación de una circunferencia.
50. Usa las ecuaciones del problema anterior para encontrar un conjunto de ecuaciones paramétricas para una circunferencia cuyo radio es 5 unidades y cuyo centro es (−2, 3).
Para los siguientes ejercicios, use una herramienta gráfica para graficar la curva representada por las ecuaciones paramétricas e identificar la curva a partir de su ecuación.
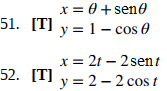
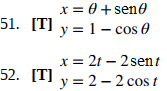


54. Un avión que viaja horizontalmente a 100 m/s sobre un terreno plano a una altura de 4000 metros debe dejar caer un paquete de emergencia sobre un objetivo en el suelo. La trayectoria del paquete viene dada por x = 100t, y = −4.9t² + 4000, t ≥ 0 donde el origen es el punto en el suelo directamente debajo del avión en el momento del lanzamiento. ¿Cuántos metros horizontales antes del objetivo debe soltarse el paquete para alcanzar el objetivo?
55. La trayectoria de una bala está dada por x = v₀ (cosα) t, y = v₀ (senα) t − (1/2)gt² donde v₀ = 500 m/s, g = 9,8 = 9,8 m/s² y α = 30 grados. ¿Cuándo golpeará el suelo la bala? ¿A qué distancia del arma golpeará el suelo la bala?
56. [T] Utilice la tecnología para trazar la curva representada por x = sen(4t), y = sen(3t), 0 ≤ t ≤ 2π.
57. [T] Utilice la tecnología para dibujar x = 2tan(t), y = 3sec(t), – π < t < π.
58. Dibuje la curva conocida como epitrocoide, que da la trayectoria de un punto en un círculo de radio b mientras rueda por fuera de un círculo de radio a. Las ecuaciones son
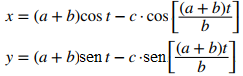
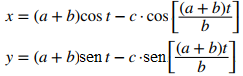
Sea a = 1, b = 2, c = 1.
59. [T] Usa la tecnología para dibujar la curva en espiral dada por x = tcos(t), y = tsen(t) de −2π ≤ t ≤ 2π.
60. [T] Utilice la tecnología para graficar la curva dada por las ecuaciones paramétricas x = 2cot(t), y = 1 − cos(2t), −π/2 ≤ t ≤ π/2. Esta curva se conoce como la bruja de Agnesi.
61. [T] Dibuja la curva dada por ecuaciones paramétricas
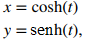
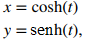
donde −2 ≤ t ≤ 2.

x=2cost,
y=8sint
Donde puedo encontrar las respuestas de los ejercicios propuesto por el cap 8.1 ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
Buen trabajo, felicitaciones
Gracias. 👍
Exelente.
Excelente información
Gracias. Es con mucho gusto! 😺👀
Muy buena información y muchas gracias por su trabajo ha sido muy util.
∑Gracias por el comentario!∞