Concavidad y puntos de inflexión
Ahora sabemos cómo determinar dónde una función está creciendo o decreciendo. Sin embargo, hay otro tema a considerar con respecto a la forma del gráfico de una función. Si el gráfico se curva, ¿se curva hacia arriba o hacia abajo? Esta noción se llama concavidad de la función.
La figura 4.18 (a) muestra una función f con una gráfica que se curva hacia arriba. A medida que x aumenta, la pendiente de la recta tangente aumenta. Por lo tanto, dado que la derivada aumenta a medida que x aumenta, f ‘ es una función creciente. Decimos que esta función f es cóncava hacia arriba. La figura 4.18 (b) muestra una función f que se curva hacia abajo. A medida que x aumenta, la pendiente de la recta tangente disminuye. Como la derivada disminuye a medida que aumenta x, f ‘ es una función decreciente. Decimos que esta función f es cóncava hacia abajo.
Definición 4.5.1. Concavidad
Sea f una función que se puede diferenciar en un intervalo abierto I. Si f ′ aumenta sobre I, decimos que f es cóncavo hacia arriba sobre I. Si f ′ disminuye sobre I, decimos que f es cóncavo hacia abajo sobre I.
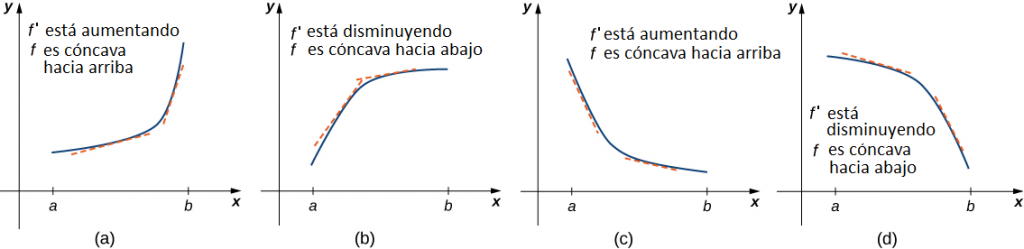
En general, sin tener la gráfica de una función f, ¿cómo podemos determinar su concavidad? Por definición, una función f es cóncava hacia arriba si f ‘ está aumentando. Por el Corolario 3, sabemos que si f ‘ es una función diferenciable, entonces f ‘ aumenta si su segunda derivada f ” (x) > 0. Por lo tanto, una función f que es dos veces diferenciable es cóncava hacia arriba cuando f ” (x) > 0. Del mismo modo, una función f es cóncava hacia abajo si f ‘ está disminuyendo. Sabemos que una función diferenciable f ‘ está disminuyendo si su segunda derivada f ” (x) < 0. Por lo tanto, una función dos veces diferenciable f es cóncava hacia abajo cuando f ” (x) < 0. La aplicación de esta lógica se conoce como prueba de concavidad.
Teorema 4.5.2. Prueba de concavidad
Sea f una función que es dos veces diferenciable en un intervalo I.
(i) Si f ”(x) > 0 para todo x ∈ I, entonces f es cóncava hacia arriba sobre I.
(ii) Si f ”(x) < 0 para todo x ∈ I, entonces f es cóncava hacia abajo sobre I.
Concluimos que podemos determinar la concavidad de una función f observando la segunda derivada de f. Además, observamos que una función f puede cambiar la concavidad (Figura 4.19). Sin embargo, una función continua puede cambiar la concavidad solo en un punto x si f ” (x) = 0 o f ” (x) no está definido. En consecuencia, para determinar los intervalos donde una función f es cóncava hacia arriba y hacia abajo, buscamos aquellos valores de x donde f ” (x) = 0 o f ” (x) no está definida. Cuando hemos determinado estos puntos, dividimos el dominio de f en intervalos más pequeños y determinamos el signo de f ” sobre cada uno de estos intervalos más pequeños. Si f ” cambia de signo cuando pasamos por un punto x, entonces f cambia la concavidad. Es importante recordar que una función f puede no cambiar la concavidad en un punto x incluso si f ”(x) = 0 o f ”(x) no está definida. Sin embargo, si f cambia la concavidad en un punto a y f es continuo en a, decimos que el punto (a, f(a)) es un punto de inflexión de f.
Definición 4.5.2. Punto de inflexión
Si f es continua en a y f cambia la concavidad en a, el punto (a, f (a)) es un punto de inflexión de f.


Ahora resumimos, en la Tabla 4.1, la información que las derivadas primera y segunda de una función f proporcionan sobre la gráfica de f, e ilustramos esta información en la Figura 4.20.
| Signo de f ‘ | ‘Signo de f ” | ¿f aumenta o disminuye? | Concavidad |
| Positivo | Positivo | Aumenta | Cóncava hacia arriba |
| Positivo | Negativo | Aumenta | Cóncava hacia abajo |
| Negativo | Positivo | Disminuye | Cóncava hacia arriba |
| Negativo | Negativo | Disminuye | Cóncava hacia abajo |
Tabla 4.1 Lo que nos dicen las derivadas sobre las gráficas


Prueba de la segunda derivada
La prueba de la primera derivada proporciona una herramienta analítica para encontrar extremos locales, pero la segunda derivada también se puede usar para localizar valores extremos. Usar la segunda derivada a veces puede ser un método más simple que usar la primera derivada.
Sabemos que si una función continua tiene extremos locales, debe ocurrir en un punto crítico. Sin embargo, una función no necesita tener extremos locales en un punto crítico. Aquí examinamos cómo se puede usar la prueba de la segunda derivada para determinar si una función tiene un extremo local en un punto crítico. Sea f una función dos veces diferenciable de tal manera que f ′(a) = 0 y f ” es continua durante un intervalo abierto I que contiene a a. Supongamos que f ”(a) < 0. Como f ” es continua sobre I, f ”(x) < 0 para todo x ∈ I (Figura 4.21). Luego, según el Corolario 3, f ′ es una función decreciente sobre I. Como f ′ (a) = 0, concluimos que para todos x ∈ I, f ′ (x) > 0 si x < a y f ′ (x) < 0 si x > a. Por lo tanto, mediante la prueba de la primera derivada, f tiene un máximo local en x = a. Por otro lado, supongamos que existe un punto b tal que f ′(b) = 0 pero f ”(b) > 0. Como f ” es continuo en un intervalo abierto I que contiene a b, entonces f ” (x) > 0 para todo x ∈ I (Figura 4.20). Luego, según el Corolario 3, f ′ es una función creciente sobre I. Como f ′(b) = 0, concluimos que para todos x ∈ I, f ′(x) < 0 si x < b y f ′ (x) > 0 si x > b. Por lo tanto, mediante la prueba de la primera prueba derivada, f tiene un mínimo local en x = b.


Figura 4.20 Considere una función dos veces diferenciable f tal que f ” sea continua. Como f ‘(a) = 0 y f ”(a) < 0, hay un intervalo I que contiene a a tal que para todo x en I, f aumenta si x < a y f disminuye si x > a. Como resultado, f tiene un máximo local en x = a. Dado que f ‘(b) = 0 y f ”(b) > 0, hay un intervalo I que contiene a b tal que para todas las x en I, f disminuye si x < b y f aumenta si x > b. Como resultado, f tiene un mínimo local en x = b.
Teorema 4.5.3. Prueba de la segunda derivada
Supongamos que f ′(c) = 0, f ” es continua en un intervalo que contiene c.
(i) Si f ”(c) > 0, entonces f tiene un mínimo local en c.
(ii) Si f ”(c) < 0, entonces f tiene un máximo local en c.
(iii) Si f ”(c) = 0, entonces la prueba no es concluyente.
Tenga en cuenta que para el caso (iii) cuando f ”(c) = 0, entonces f puede tener un máximo local, un mínimo local, o ninguno en c. Por ejemplo, las funciones f (x) = x3, f (x) = x4 y f (x) = – x4 tienen puntos críticos en x = 0. En cada caso, la segunda derivada es cero en x = 0. Sin embargo, la función f (x) = x4 tiene un mínimo local en x = 0, mientras que la función f (x) = – x4 tiene un máximo local en x, y la función f (x) = x3 no tiene un extremo local en x = 0.
Ahora hemos desarrollado las herramientas que necesitamos para determinar dónde una función está creciendo y decreciendo, así como también hemos adquirido una comprensión de la forma básica de la gráfica de una función. En la siguiente sección discutimos lo que le sucede a una función cuando x → ± ∞. En ese momento, tendremos suficientes herramientas para proporcionar gráficas precisos de una gran variedad de funciones.
