Vectores tangentes y vectores tangentes unitarios
Recuerde de la Introducción a las Derivadas que la derivada en un punto puede interpretarse como la pendiente de la recta tangente a la gráfica en ese punto. En el caso de una función de valor vectorial, la derivada proporciona un vector tangente a la curva representada por la función. Considere la función de valor vectorial r (t) = cost i + sent j. La derivada de esta función es r ′ (t) = – sent i + cost j. Si sustituimos el valor t = π / 6 en ambas funciones obtenemos


La gráfica de esta función aparece en la Figura 10.9_1, junto con los vectores r (π/6) y r ′ (π/6).

Observe que el vector r ′ (π/6) es tangente a la circunferencia en el punto correspondiente a t = π / 6. Este es un ejemplo de un vector tangente a la curva plana definida por r (t) = cost i + sent j.
DEFINICIÓN. Vector tangente de la unidad principalSea C una curva definida por una función de valor vectorial r, y suponga que r ‘(t) existe cuando t = t0. Un vector tangente v en t = t0 es cualquier vector tal que, cuando la cola del vector se coloca en el punto r (t0) en la gráfica, el vector v es tangente a la curva C. El vector r ‘(t0) es un ejemplo de un vector tangente en el punto t = t0. Además, suponga que r ′ (t) ≠ 0. El vector tangente de la unidad principal en t se define como
con ∥ r ′ (t) ∥ ≠ 0. |
El vector unitario tangente es exactamente lo que parece: un vector unitario que es tangente a la curva. Para calcular un vector tangente unitario, primero encuentre la derivada r ‘(t). Segundo, calcule la magnitud de la derivada. El tercer paso es dividir la derivada por su magnitud.
EJEMPLO ILUSTRATIVO 10.9_4. Encontrar un vector tangente unitario
Encuentre el vector tangente unitario para cada una de las siguientes funciones vectoriales:
a. r (t) = cost i + sent j
b. u (t) = (3t ² + 2t) i + (2 − 4t ³) j + (6t + 5) k
Solución:
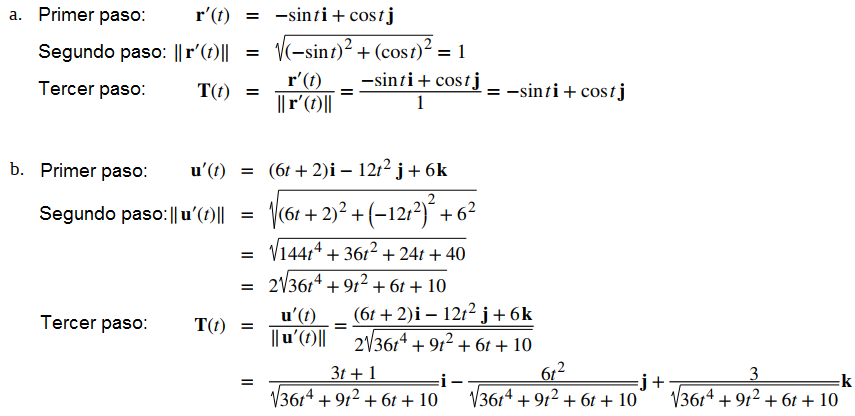
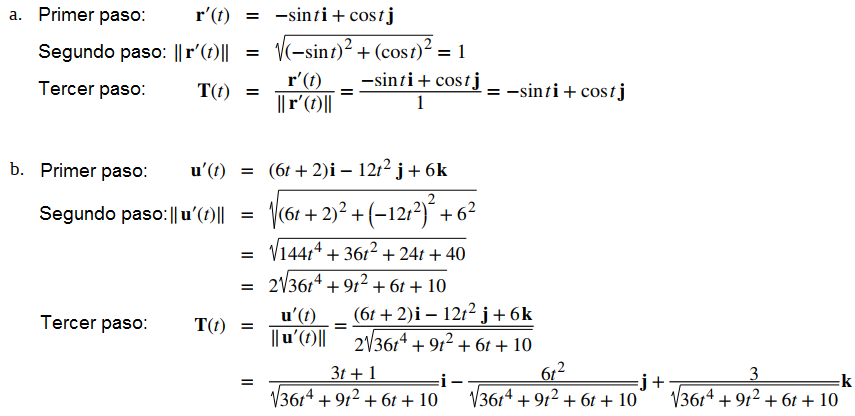
Integrales de funciones vectoriales
Introdujimos antiderivadas de funciones de valor real en Antiderivadas e integrales definidas de funciones de valor real en La integral definida. Cada uno de estos conceptos se puede extender a funciones con valores vectoriales. Además, así como podemos calcular la derivada de una función con valor vectorial diferenciando las funciones componentes por separado, podemos calcular la antiderivada de la misma manera. Además, el teorema fundamental del cálculo se aplica también a las funciones de valor vectorial.
La antiderivada de una función de valor vectorial aparece en las aplicaciones. Por ejemplo, si una función de valor vectorial representa la velocidad de un objeto en el tiempo t, entonces su antiderivada representa la posición. O, si la función representa la aceleración del objeto en un momento dado, entonces la antiderivada representa su velocidad.
DEFINICIÓN. Integral indefinida y definida de una función de valor vectorialSean f, g y h funciones integrables de valor real durante el intervalo cerrado [a, b].
La integral definida de una función vectorial es
2. La integral indefinida de una función de valor vectorial r (t) = f (t) i + g (t) j + h (t) k es
La integral definida de la función vectorial es
|
Dado que la integral indefinida de una función de valor vectorial implica integrales indefinidas de las funciones componentes, cada una de estas integrales componentes contiene una constante de integración. Todas pueden ser diferentes. Por ejemplo, en el caso bidimensional, podemos tener


donde F y G son las antiderivadas de f y g, respectivamente. Luego


donde C = C1i + C2j. Por lo tanto, la constante de integración se convierte en un vector constante.
EJEMPLO ILUSTRATIVO 10.9_5. Integrando funciones vectoriales
Calcule cada una de las siguientes integrales:
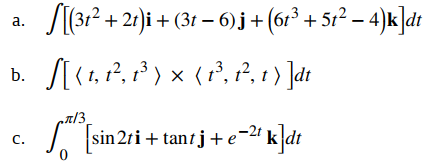
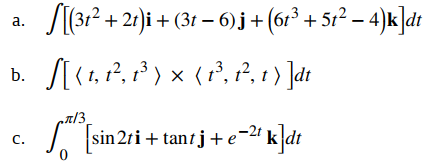
Solución:
a. Usamos la primera parte de la definición de la integral de una curva espacial:


b. Primero calcule ⟨t, t ², t ³⟩ × ⟨t ³, t ², t⟩:


Luego, sustituya esto nuevamente en la integral e integre:


c. Use la segunda parte de la definición de la integral de una curva espacial:




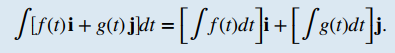



Great content! Super high-quality! Keep it up! 🙂
Ty!