Diferenciales
Hemos visto que las aproximaciones lineales se pueden usar para estimar valores de funciones. También se pueden usar para estimar la cantidad que cambia el valor de una función como resultado de un pequeño cambio en la entrada. Para discutir esto más formalmente, definimos un concepto relacionado: diferenciales. Los diferenciales nos proporcionan una forma de estimar la cantidad que cambia una función como resultado de un pequeño cambio en los valores de entrada.
En el capítulo anterior cuando estudiamos las derivadas, se utilizó la notación de Leibniz dy/dx para representar la derivada de y con respecto a x. Aunque usamos las expresiones dy y dx en esta notación, no tenían significado por sí mismas. Aquí damos un significado para las expresiones dy y dx por separado. Supongamos que y = f (x) es una función diferenciable. Sea dx una variable independiente a la que se le puede asignar cualquier número real distinto de cero y definamos la variable dependiente dy por
| dy = f ′(x) dx. | (4.2) |
Es importante notar que dy es una función de x y dx. Las expresiones dy y dx se llaman diferenciales. Podemos dividir ambos lados de la ecuación anterior por dx, de lo que resulta


Esta es la expresión familiar que hemos usado para denotar una derivada. La ecuación 4.2 se conoce como la forma diferencial de la ecuación 4.3.
EJEMPLO ILUSTRATIVO 4.2_4. Cálculo de diferenciales
Para cada una de las siguientes funciones, encuentre dy y evalúe cuando x = 3 y dx = 0.1.
a. y = x² + 2x
b. y = cosx
Solución:
El paso clave es calcular la derivada. Cuando tenemos eso, podemos obtener dy directamente.
a. Como f (x) = x² + 2x, sabemos que f ′(x) = 2x + 2, y por lo tanto
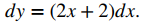
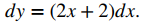
Cuando x = 3 y dx = 0.1,
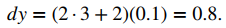
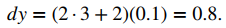
b. Como f (x) = cosx, f ′(x) = – sen(x). Esto nos da
dy = −senx dx.
Cuando x = 3 y dx = 0.1,
dy = −sen(3) (0.1) = – 0.1sen(3).
Ahora conectamos diferenciales a aproximaciones lineales. Los diferenciales se pueden usar para estimar el cambio en el valor de una función resultante de un pequeño cambio en los valores de entrada. Considere una función f que es diferenciable en el punto a. Suponga que la entrada x cambia en una pequeña cantidad. Estamos interesados en cuánto cambia la salida y. Si x cambia de a a a + dx, entonces el cambio en x es dx (también denotado Δx), y el cambio en y viene dado por
Δy = f (a + dx) − f (a).
Sin embargo, en lugar de calcular el cambio exacto en y, a menudo es más fácil aproximar el cambio en y utilizando una aproximación lineal. Para x cerca de a, f (x) se puede aproximar por la aproximación lineal
L (x) = f (a) + f ‘(a) (x − a).
Por lo tanto, si dx es pequeño,
f (a + dx) ≈ L (a + dx) = f (a) + f ‘(a) (a + dx − a).
Es decir,
f (a + dx) − f (a) ≈ L (a + dx) − f (a) = f ‘(a) dx.
En otras palabras, el cambio real en la función f si x aumenta de a a a + dx es aproximadamente la diferencia entre L (a + dx) y f (a), donde L (x) es la aproximación lineal de f en a. Por definición de L (x), esta diferencia es igual a f ‘(a) dx. En resumen,
Δy = f (a + dx) − f (a) ≈ L (a + dx) − f (a) = f ‘(a) dx = dy.
Por lo tanto, podemos usar el diferencial dy = f ‘(a) dx para aproximar el cambio en y si x aumenta de x = a a x = a + dx. Podemos ver esto en la siguiente gráfica.


En los videos veremos cómo usar diferenciales para aproximar el cambio en el valor de la función que resulta de un pequeño cambio en el valor de la entrada. Tenga en cuenta que el cálculo con diferenciales es mucho más simple que calcular los valores reales de las funciones y el resultado está muy cerca de lo que obtendremos con el cálculo más exacto.
EJEMPLO ILUSTRATIVO 4.2_5. Cambio aproximado con diferenciales
Sea y = x² + 2x. Calcule Δy y dy en x = 3 si dx = 0.1.
Solución:
El cambio real en y si x cambia de x = 3 a x = 3.1 viene dado por


El cambio aproximado en y viene dado por dy = f ′(3) dx. Como f ′(x) = 2x + 2, tenemos
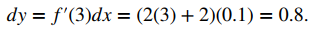
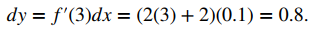
Calculando el grado de error en una medición
Cualquier tipo de medición es propensa a una cierta cantidad de error. En muchas aplicaciones, ciertas cantidades se calculan en función de las mediciones. Por ejemplo, el área de un círculo se calcula midiendo el radio del círculo. Un error en la medición del radio conduce a un error en el valor calculado del área. Aquí examinamos este tipo de error y estudiamos cómo se pueden usar los diferenciales para estimar el error.
Considere una función f con una entrada que es una cantidad medida empíricamente. Suponga que el valor exacto de la cantidad medida es a, pero el valor medido es a + dx. Decimos que el error de medición es dx (o Δx). Como resultado, se produce un error en la cantidad calculada f (x). Este tipo de error se conoce como error propagado y viene dado por
Δy = f (a + dx) − f (a).
Como todas las mediciones son propensas a algún grado de error, no conocemos el valor exacto de una cantidad medida, por lo que no podemos calcular el error propagado exactamente. Sin embargo, dada una estimación de la precisión de una medición, podemos usar diferenciales para aproximar el error propagado Δy. Específicamente, si f es una función diferenciable en a, el error propagado es
Δy ≈ dy = f ′(a) dx.
Desafortunadamente, no sabemos el valor exacto de a. Sin embargo, podemos usar el valor medido a + dx y estimar
Δy ≈ dy = f ′(a + dx) dx.
En el siguiente ejemplo, observamos cómo se pueden usar los diferenciales para estimar el error al calcular el volumen de una caja si asumimos que la medición de la longitud del lado se realiza con cierta precisión.
EJEMPLO ILUSTRATIVO 4.2_6. Volumen de un cubo
Suponga que la longitud lateral de un cubo se mide en 5 cm con una precisión de 0.1 cm.
a. Use diferenciales para estimar el error en el volumen calculado del cubo.
b. Calcule el volumen del cubo si la longitud del lado es (i) 4.9 cm y (ii) 5.1 cm para comparar el error estimado con el error potencial real.
Solución:
a. La medida de la longitud del lado es precisa dentro de ± 0.1 cm. Por lo tanto,


El volumen de un cubo viene dado por V = x³, lo que lleva a
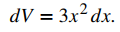
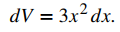
Usando la longitud lateral medida de 5 cm, podemos estimar que


Por lo tanto,
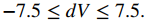
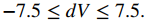
b. Si la longitud del lado es en realidad 4,9 cm, entonces el volumen del cubo es
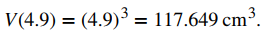
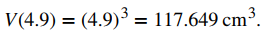
Si la longitud lateral es en realidad de 5,1 cm, entonces el volumen del cubo es
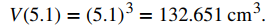
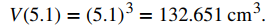
Por lo tanto, el volumen real del cubo está entre 117.649 y 132.651. Dado que la longitud del lado se mide en 5 cm, el volumen calculado es V(5) = 5³ = 125. Por lo tanto, el error en el volumen calculado es
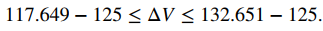
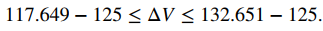
Es decir,


Vemos que el error estimado dV está relativamente cerca del error potencial real en el volumen calculado.
Error absoluto y error relativo
El error de medición dx (= Δx) y el error propagado Δy son errores absolutos. Normalmente estamos interesados en el tamaño de un error en relación con el tamaño de la cantidad que se mide o calcula. Dado un error absoluto Δq para una cantidad particular, definimos el error relativo como Δq/q, donde q es el valor real de la cantidad. El error porcentual es el error relativo expresado como un porcentaje. Por ejemplo, si medimos la altura de una escalera de 63 pulgadas cuando la altura real es 62 pulgadas, el error absoluto es 1 pulgada pero el error relativo es 1/62 = 0.016, o 1.6%. En comparación, si medimos que el ancho de un pedazo de cartón es de 8.25 pulgadas cuando el ancho real es de 8 pulgadas, nuestro error absoluto es de 14 pulgadas, mientras que el error relativo es 0.25/8 = 1/32, o 3.1%. Por lo tanto, el porcentaje de error en la medición del cartón es mayor, aunque 0.25 pulg. Sea menor que 1 pulg.
EJEMPLO ILUSTRATIVO 4.2_7. Error relativo y porcentual
Un astronauta que usa una cámara mide el radio de la Tierra como 4000 mi con un error de ± 80 mi. Usemos diferenciales para estimar el error relativo y el porcentaje de error al usar esta medida de radio para calcular el volumen de la Tierra, suponiendo que el planeta sea una esfera perfecta.
Solución:
Si la medida del radio es precisa dentro de ± 80, tenemos
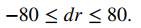
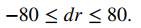
Dado que el volumen de una esfera está dado por
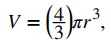
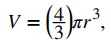
Tenemos que
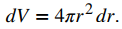
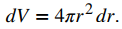
Usando el radio medido de 4000 mi, podemos estimar
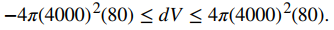
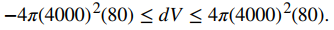
Para estimar el error relativo, considere dV/V. Como no conocemos el valor exacto del volumen V, use el radio medido r = 4000 mi para estimar V. Obtenemos
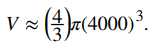
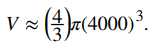
Por lo tanto, el error relativo satisface


que se simplifica a


El error relativo es 0.06 y el error porcentual es 6%.

Muchas gracias por la información, me ha sido de gran utilidad.
Muy bien! 👍