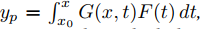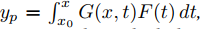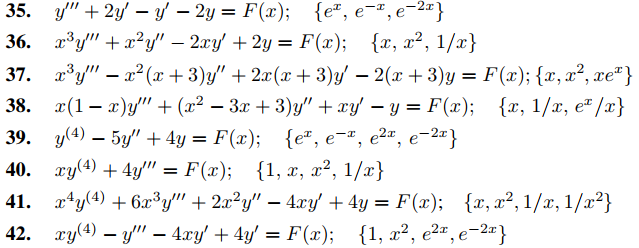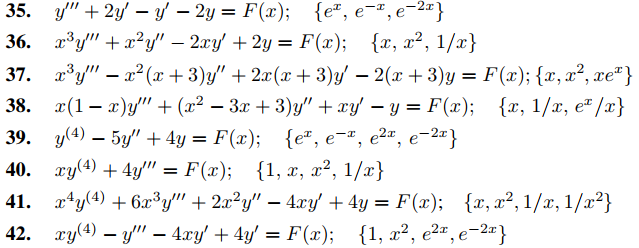| 9. Ecuaciones diferenciales | 9.9. Ecuaciones lineales de orden superior | 9.9.4 Variación de parámetros para ecuaciones de orden superior |

Ejercicios propuestos para la sección 9.9.4

      En los ejercicios 1 a 21 encuentre una solución particular, dado el conjunto fundamental de soluciones de la ecuación complementaria

 

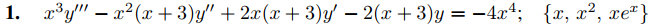
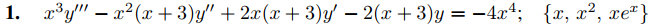
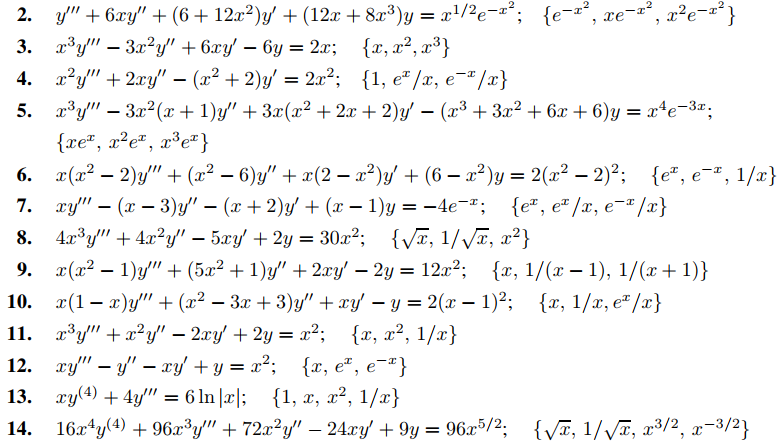
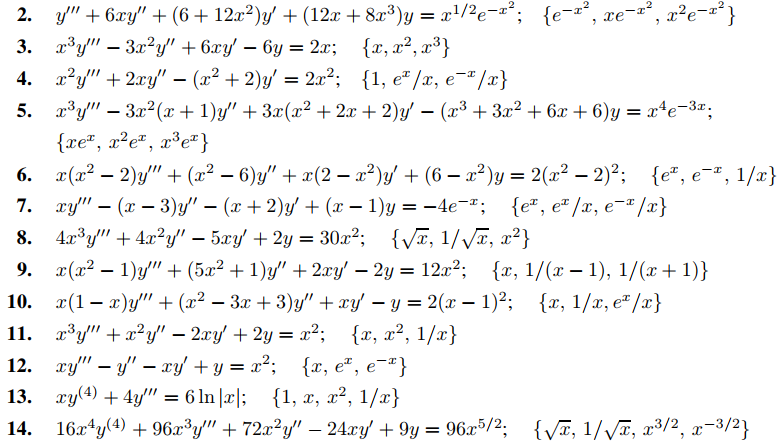
      En los ejercicios 22 a 33, resuelva el problema con valores iniciales, dado el conjunto fundamental de soluciones de la ecuación complementaria. Donde lo indique C/G, grafique la solución.

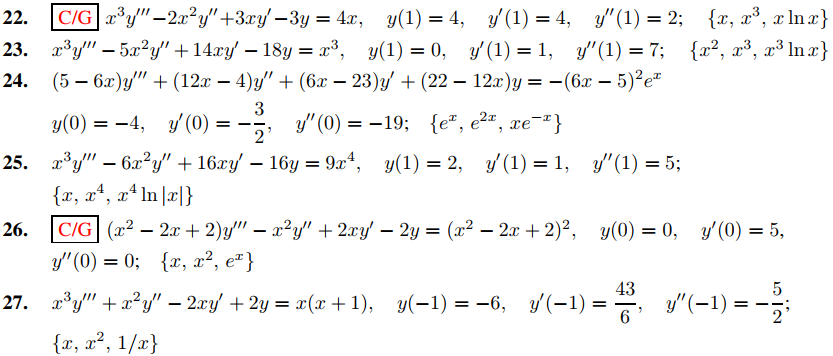
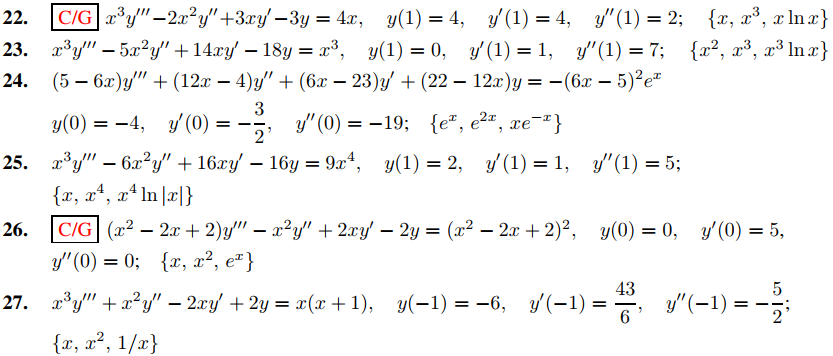
34. Supongamos que la ecuación

       (A)

es normal en un intervalo (a, b). Sea {y₁, y₂, . . ., y_n} un conjunto fundamental de soluciones de su ecuación complementaria en (a, b), sea W el wronskiano de {y₁, y₂, . . ., y_n}, y sea W_j el determinante obtenido al eliminar la última fila y la j-ésima columna de W. Supongamos que x₀ está en (a, b), sea

y definamos

y_p = u₁y₁ + u₂y₂ + · · · + u_ny_n.

(a) Demuestre que y_p es una solución de (A) y que

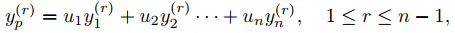
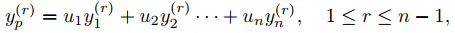
y

SUGERENCIA: Consulte la derivación del método de variación de parámetros al comienzo de la sección.

(b) Demuestre que y_p es la solución del problema con valores iniciales

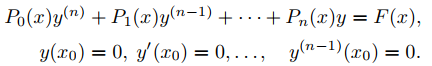
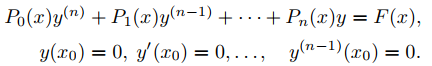
(c) Demuestre que y_p se puede escribir como

donde

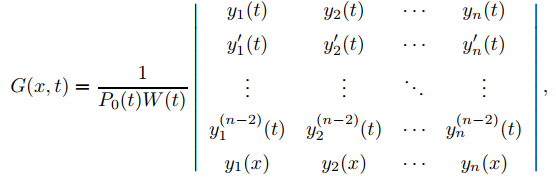
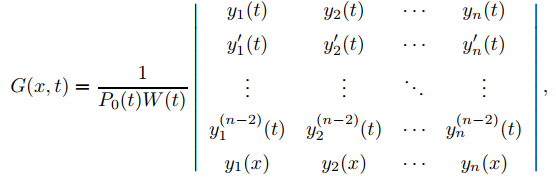
que se llama función de Green para (A).

(d) Demuestre que

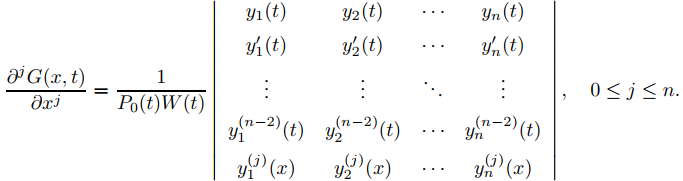
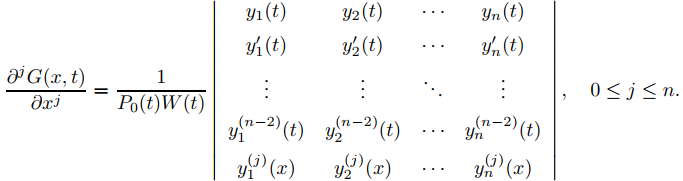
(e) Demuestre que si a < t < b entonces

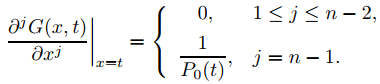
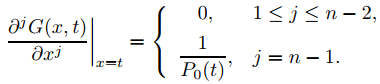
(f) Demuestre que

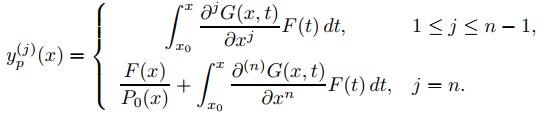
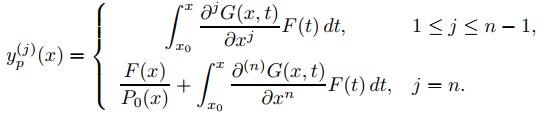
      En los ejercicios 35 a 42, utilice el método sugerido en el ejercicio 34 para encontrar una solución particular en la forma dado el conjunto fundamental de soluciones indicado. Suponga que x y x₀ están en un intervalo en el que la ecuación es normal.