Ejercicios propuestos para el Capítulo 9.8.1
1. Encuentra las transformadas de Laplace de las siguientes funciones evaluando la integral 
2. Usa la tabla de transformadas de Laplace para encontrar las transformadas de Laplace de las siguientes funciones.
para cada número real s.
4. Grafique las siguientes funciones continuas por partes y evalúe f (t +), f (t−) y f (t) en cada punto de discontinuidad.
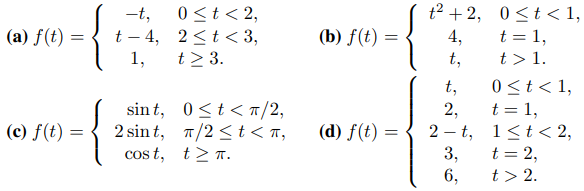
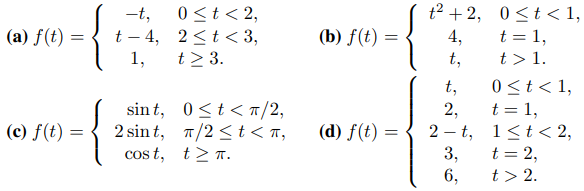
5. Encuentra la transformada de Laplace:
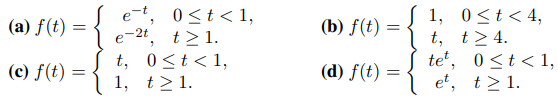
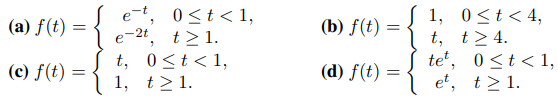
6. Demuestre que si f (t) ↔ F(s) entonces tk f (t) ↔ (−1)kF(k)(s). SUGERENCIA: Suponga que está permitido diferenciar la integral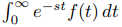 
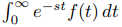
con respecto a s bajo el signo integral.
7. Utilice las transformadas de Laplace conocidas
y 
y el resultado del Ejercicio 6 para encontrar 
(teλt cos ωt) y (teλt sen ωt).
8. Utilice la transformada de Laplace conocida (1) = 1/s y el resultado del Ejercicio 6 para demostrar que
entero.
9. (a) Demuestre que si 
existe y es finito, entonces f es de orden exponencial s0.
(b) Demuestre que si f es de orden exponencial s0 entonces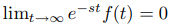 
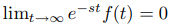
para todos los s > s0.
(c) Muestre que si f es de orden exponencial s0 y g(t) = f (t + τ) donde τ > 0, entonces g también es de orden exponencial s0.
10. Recuerde el siguiente teorema del cálculo.
Teorema A. Sea g integrable en [0, T] para todo T > 0. Suponga que hay una función w definida en algún intervalo [τ, ∞) (con τ ≥ 0) tal que | g(t) | ≤ w(t) para t ≥ τ y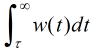 
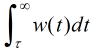
converge, entonces 
converge.
Utilice el Teorema A para demostrar que si f es continua por partes en [0, ∞) y de orden exponencial s0, entonces f tiene una transformada de Laplace F(s) definida para s > s0.
11. Demuestre: Si f es continuo por partes y de orden exponencial, entonces lims → ∞ F(s) = 0.
12. Demuestre: Si f es continua en [0, ∞) y de orden exponencial s0 > 0, entonces
SUGERENCIA: Utilice la integración por partes para evaluar la transformada de la izquierda.
13. Suponga que f es continua por partes y de orden exponencial, y que limt → 0+ f (t)/t existe. Muestre que
SUGERENCIA: Utilice los resultados de los Ejercicios 6 y 11.
14. Suponga que f es continua por tramos en [0, ∞).
(a) Demuestre: Si la integral 
satisface la desigualdad | g(t) | ≤ M(t ≥ 0), entonces f tiene una transformada de Laplace F(s) definida para s > s0. SUGERENCIA: Utilice la integración por partes para demostrar que
(b) Muestre que si ( f ) existe para s = s0, entonces existe para s > s0. Demuestre que la función
tiene una transformada de Laplace definida para s > 0, aunque f no es de orden exponencial.
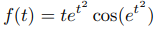
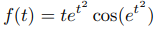
tiene una transformada de Laplace definida para s > 0, aunque f no es de orden exponencial.
15. Utilice la tabla de transformadas de Laplace y el resultado del Ejercicio 13 para encontrar las transformadas de Laplace de las siguientes funciones.
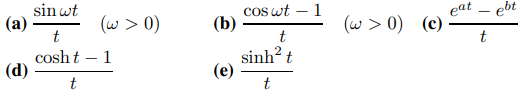
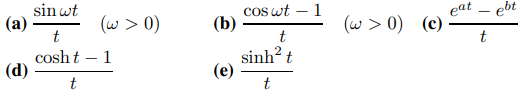
16. La función gamma está definida por
que se puede demostrar que converge si α > 0.
(a) Utilice la integración por partes para demostrar que
Γ(α + 1) = αΓ(α), α > 0.
(b) Demuestre que Γ(n + 1) = n! si n = 1, 2, 3 ,. . . .
(c) De (b) y la tabla de transformadas de Laplace,
si α es un número entero no negativo. Demuestre que esta fórmula es válida para cualquier α > −1. AYUDA: Cambie la variable de integración en la integral por Γ(α + 1).
17. Suponga que f es continua en [0, T] y f (t + T) = f (t) para todo t ≥ 0. (En este caso, decimos que f es periódica con el período T.)
(a) Concluya del Teorema 9.8.1.6 que la transformada de Laplace de f se define para s > 0. AYUDA: Dado que f es continua en [0, T] y periódica con el período T, está acotada en [0, ∞).
(b) Demuestre que
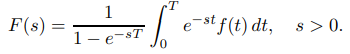
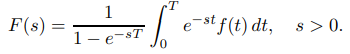
SUGERENCIA: Escriba
Entonces muestre que
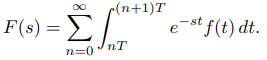
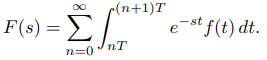
y recuerde la fórmula para la suma de una serie geométrica.
18. Use la fórmula dada en el Ejercicio 17 (b) para encontrar las transformadas de Laplace de las funciones periódicas dadas:
