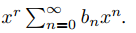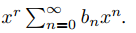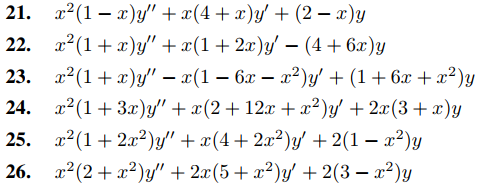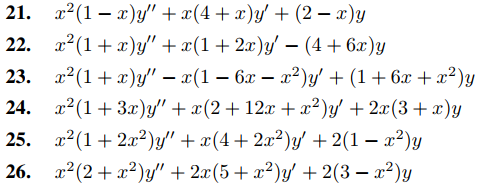| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.1. Revisión de series de potencias |

Ejercicios propuestos para el Capítulo 9.7.1

1. Para cada serie de potencias, use el Teorema 9.7.1.2 para encontrar el radio de convergencia R. Si R > 0, encuentre el intervalo abierto de convergencia.

2. Supongamos que hay un entero M tal que b_m ≠ 0 para m ≥ M, y

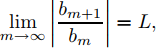
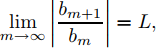
donde 0 ≤ L ≤ ∞. Demuestre que el radio de convergencia de

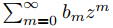
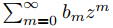
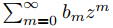
es R = 1/√L, lo que se interpreta como que R = 0 si L = ∞ o R = ∞ si L = 0. AYUDA: aplique el Teorema 9.7.1.2 a la serie y luego sea z = (x − x₀)².

3. Para cada serie de potencias, use el resultado del ejercicio 2 para encontrar el radio de convergencia R. Si R > 0, encuentre el intervalo abierto de convergencia.

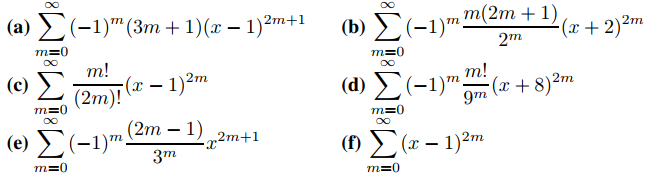
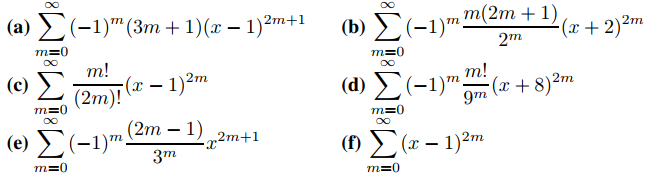
4. Supongamos que hay un entero M tal que b_m ≠ 0 para m ≥ M, y

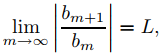
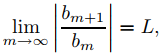
donde 0 ≤ L ≤ ∞. Sea k un entero positivo. Demuestre que el radio de convergencia de

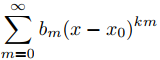
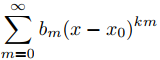
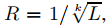
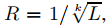
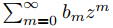
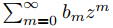
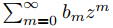
es que se interpreta como que R = 0 si L = ∞ o R = ∞ si L = 0. AYUDA: Aplique el Teorema 9.7.1.2 a la serie y luego sea z = (x − x₀)^k.

5. Para cada serie de potencias, use el resultado del ejercicio 4 para encontrar el radio de convergencia R. Si R > 0, encuentre el intervalo abierto de convergencia.

6. L Grafique y = senx y el polinomio de Taylor

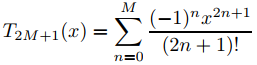
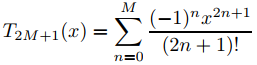
en el intervalo (−2π, 2π) para M = 1, 2, 3, . . . , hasta que encuentre un valor de M para el cual no haya una diferencia perceptible entre las dos gráficas.

7. L Grafique y = cosx y el polinomio de Taylor

en el intervalo (−2π, 2π) para M = 1, 2, 3, . . . , hasta que encuentre un valor de M para el cual no haya una diferencia perceptible entre los dos gráficos.

8. L Grafique y = 1/(1 − x) y el polinomio de Taylor

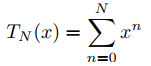
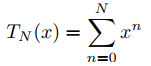
en el intervalo [0, .95] para N = 1, 2, 3, . . . , hasta que encuentre un valor de N para el cual no haya una diferencia perceptible entre los dos gráficos. Elige la escala en el eje y para que 0 ≤ y ≤ 20.

9. L Grafique y = coshx y el polinomio de Taylor

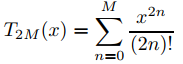
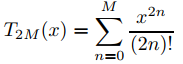
en el intervalo (−5, 5) para M = 1, 2, 3, . . . , hasta que encuentre un valor de M para el cual no haya una diferencia perceptible entre los dos gráficos. Elige la escala en el eje y para que 0 ≤ y ≤ 75.

10. L Grafique y = senhx y el polinomio de Taylor

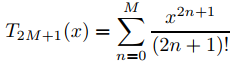
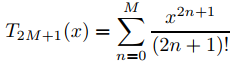
en el intervalo (−5, 5) para M = 0, 1, 2, . . . , hasta que encuentre un valor de M para el cual no haya una diferencia perceptible entre los dos gráficos. Elige la escala en el eje y para que −75 ≤ y ≤ 75.

      En los ejercicios 11 a 15, encuentre una solución en serie de potencias 

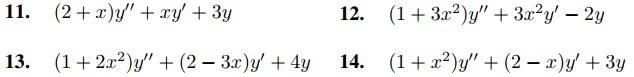
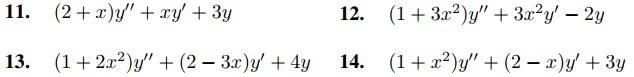
15. (1 + 3x²)y′′ − 2xy′ + 4y

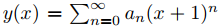
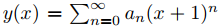
16. Supongamos en un intervalo abierto que contiene x₀ = − 1. Encuentra una serie de potencias en x + 1 para

xy′′ + (4 + 2x)y′ + (2 + x)y.

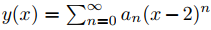
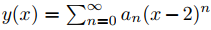
17. Supongamos en un intervalo abierto que contiene x₀ = 2. Encuentra una serie de potencias en x − 2 para

x²y′′ + 2xy′ − 3xy.

18. L Haz el siguiente experimento para varias opciones de números reales a₀ y a₁.

(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial

(2 − x)y′′ + 2y = 0,   y(0) = a₀,  y′(0) = a₁,

numéricamente en (−1.95, 1.95). Elija el método más preciso que proporcione su paquete de software. (Consulte la Sección 9.10.1 para una breve discusión de uno de estos métodos).

(b) Para N = 2, 3, 4, . . . , calcule a₂, . . . , a_N de la ecuación (9.7.1.18) y graficar

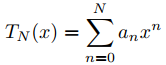
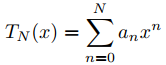
y la solución obtenida en (a) en los mismos ejes. Continúe aumentando N hasta que sea obvio que no tiene sentido continuar. (Esto suena vago, pero sabrá cuándo detenerse).

19. L Siga las instrucciones del ejercicio 18 para el problema de valor inicial

(1 + x)y′′ + 2(x − 1)²y′ + 3y = 0,   y(1) = a₀, y′(1) = a₁,

en el intervalo (0, 2). Utilice ecuaciones. (9.7.1.24) y (9.7.1.25) para calcular {a_n}.

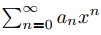
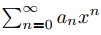
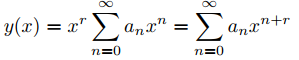
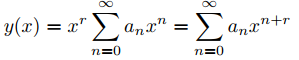
20. Supongamos que la serie converge en un intervalo abierto (−R, R), sea r un número real arbitrario y defina

en (0, R). Use el Teorema 9.7.1.4 y la regla para derivar el producto de dos funciones para demostrar que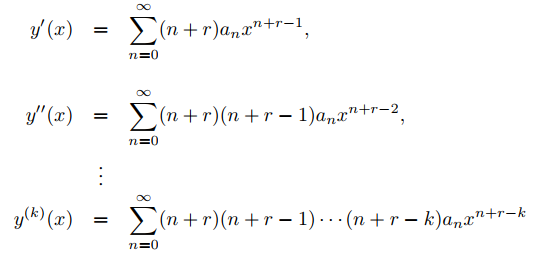
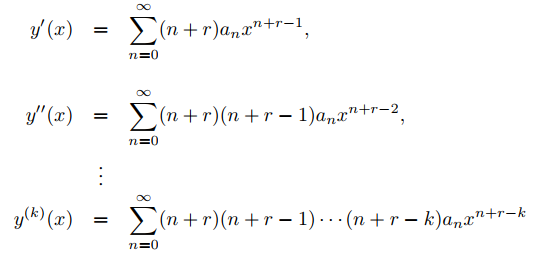
en (0, R).

      En los ejercicios 21 a 26, sea y como se define en el ejercicio 20 y escriba la expresión dada en la forma