| 9. Ecuaciones diferenciales | 9.7.Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.6 El método de Frobenius II |
Ejercicios propuestos para el Capítulo 9.7.6
En los ejercicios 1 a 11, encuentre un conjunto fundamental de soluciones de Frobenius. Calcule los términos relacionados con xn + r1, donde 0 ≤ n ≤ N (N al menos 7) y r1 es la raíz de la ecuación indicial. Opcionalmente, escriba un programa de computadora para implementar las fórmulas de recurrencia aplicables y tome N > 7.


En los ejercicios 12 a 22 encuentre un conjunto fundamental de soluciones de Frobenius. Dé fórmulas explícitas para los coeficientes.


En los ejercicios 23 a 27 encuentre un conjunto fundamental de soluciones de Frobenius. Calcule los términos relacionados con xn + r1, donde 0 ≤ n ≤ N (N al menos 7) y r1 es la raíz de la ecuación indicial. Opcionalmente, escriba un programa de computadora para implementar las fórmulas de recurrencia aplicables y tome N > 7.


En los ejercicios 28 a 38 encuentre un conjunto fundamental de soluciones de Frobenius. Dé fórmulas explícitas para los coeficientes.


En los ejercicios 39 a 43 encuentre un conjunto fundamental de soluciones de Frobenius. Calcule los términos relacionados con x2m + r1, donde 0 ≤ m ≤ M (M al menos 3) y r1 es la raíz de la ecuación indicial. Opcionalmente, escriba un programa de computadora para implementar las fórmulas de recurrencia aplicables y tome M > 3.


En los ejercicios 44 a 52 encuentre un conjunto fundamental de soluciones de Frobenius. Dé fórmulas explícitas para los coeficientes.
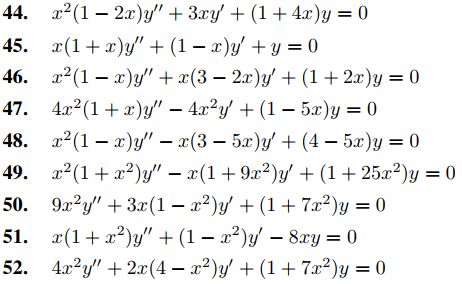
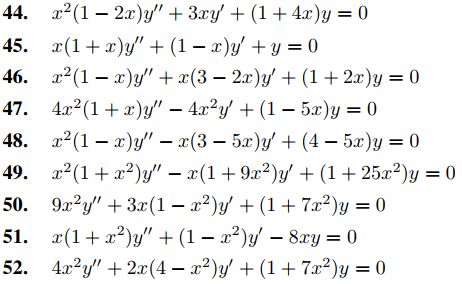
53. Bajo los supuestos del Teorema 9.7.6.2, suponga que la serie de potencias


convergen en (−ρ, ρ).
(a) Demuestre que




son linealmente independientes en (0, ρ). AYUDA: Demuestre que si c1 y c2 son constantes tales que c1y1 + c2y2 ≡ 0 en (0, ρ), entonces


Entonces, deja x → 0+ para concluir que c2 = 0.
(b) Use el resultado de (a) para completar la prueba del Teorema 9.7.6.2.
54. Sea
Ly = x2(α0 + α1x)y′′ + x(β0 + β1x)y′ + (γ0 + γ1x)y
y defina
p0(r) = α0r(r − 1) + β0r + γ0 y p1(r) = α1r(r − 1) + β1r + γ1.
El Teorema 9.7.6.1 y el ejercicio 9.7.5.55(a) implican que si


donde


entonces
Ly(x, r) = p0(r)xr.
Ahora suponga que p0(r) = α0(r − r1)2 y p1(k + r1) ≠ 0 si k es un número entero no negativo.
(a) Demuestre que Ly = 0 tiene la solución


donde


(b) Demuestre que Ly = 0 tiene la segunda solución


donde


(c) Concluya de (a) y (b) que si γ1 ≠ 0 entonces


y


son soluciones de
α0x2y′′ + β0xy′ + (γ0 + γ1x)y = 0.
(La conclusión también es válida si γ1 = 0. ¿Por qué?)
55. Sea
Ly = x2(α0 + αqxq)y′′ + x(β0 + βqxq)y′ + (γ0 + γqxq)y
donde q es un entero positivo, y definamos
p0(r) = α0r(r − 1) + β0r + γ0 y pq(r) = αqr(r − 1) + βqr + γq.
Supongamos
p0(r) = α0(r − r1)2 y pq(r) 

(a) Recuerde del Ejercicio 9.7.5.59 que Ly = 0 tiene la solución


donde


(b) Demuestre que Ly = 0 tiene la segunda solución


donde


(c) Concluya de (a) y (b) que si γq ≠ 0 entonces


y


son soluciones de
α0x2y′′ + β0xy′ + (γ0 + γqxq)y = 0.
56. La ecuación
xy′′ + y′ + xy = 0
es la ecuación de Bessel de orden cero. (Consulte el Ejercicio 53). Encuentre dos soluciones de Frobenius linealmente independientes de esta ecuación.
57. Suponga que se cumplen los supuestos del Ejercicio 9.7.5.53, excepto que
p0(r) = α0(r − r1)2.
Muestre que




son soluciones de Frobenius linealmente independientes de


en cualquier intervalo (0, ρ) en el que α0 + α1x + α2x2 no tiene ceros.
En los ejercicios 58 a 65 utilice el método sugerido por el Ejercicio 57 para encontrar la solución general en algún intervalo (0, ρ).


66. (a) Sean L y y(x, r) como en los ejercicios 57 y 58. Amplíe el teorema 9.7.6.1 demostrando que


(b) Demuestre que si
p0(r) = α0(r − r1)2
entonces
y1 = y(x, r1) y 

son soluciones de Ly = 0.
