| 9. Ecuaciones diferenciales | 9.7.Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.5. El método de Frobenius I |

Ejercicios propuestos para el Capítulo 9.7.5

      Este conjunto contiene ejercicios específicamente identificados por L que le piden que implemente el procedimiento de verificación. Estos ejercicios en particular se eligieron arbitrariamente; también puede formular tales problemas de laboratorio para cualquiera de las ecuaciones de los ejercicios 1 a 10, 14 a 25 y 28 a 51.

      En los ejercicios 1 a 10 encuentre un conjunto fundamental de soluciones de Frobenius. Calcule a₀, a₁. . . , a_N para N al menos 7 en cada solución.

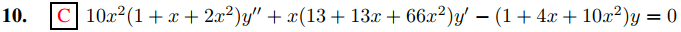
11. L Las soluciones de Frobenius de

2x²(1 + x + x²)y′′ + x(9 + 11x + 11x²)y′ + (6 + 10x + 7x²)y = 0

obtenidas en el Ejemplo 9.7.5.1 están definidas en (0, ρ), donde ρ está definida en el Teorema 9.7.5.2. Encuentre ρ. Luego haga los siguientes experimentos para cada solución de Frobenius, con M = 20 y δ = 0.5ρ, 0.7ρ y 0.9ρ en el procedimiento de verificación descrito al final de esta sección.

(a) Calcule σ_N(δ) (consulte la ecuación (7.5.28)) para N = 5, 10, 15,. . . , 50.
(b) Encuentre N tales que σ_N(δ) < 10⁻⁵.
(c) Encuentre N tal que σ_N(δ) < 10⁻¹⁰

12. L Por el Teorema 9.7.5.2 las soluciones de Frobenius de la ecuación del Ejercicio 4 se definen en (0, ∞). Realice los experimentos (a), (b) y (c) del Ejercicio 11 para cada solución de Frobenius, con M = 20 y δ = 1, 2 y 3 en el procedimiento de verificación descrito al final de esta sección.

13. L Las soluciones de Frobenius de la ecuación del ejercicio 6 se definen en (0, ρ), donde ρ se define en el teorema 9.7.5.2. Encuentre ρ y realice los experimentos (a), (b) y (c) del Ejercicio 11 para cada solución de Frobenius, con M = 20 y δ = .3ρ, .4ρ y .5ρ, en el procedimiento de verificación descrito al final de esta sección.

      En los ejercicios 14 a 25 encuentre un conjunto fundamental de soluciones de Frobenius. Dé fórmulas explícitas para los coeficientes en cada solución

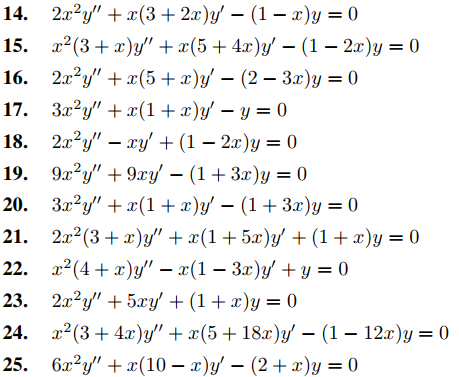
26. L Por el Teorema 9.7.5.2 las soluciones de Frobenius de la ecuación del Ejercicio 17 se definen en (0, ∞). Realice los experimentos (a), (b) y (c) del Ejercicio 11 para cada solución de Frobenius, con M = 20 y δ = 3, 6, 9 y 12 en el procedimiento de verificación descrito al final de esta sección.

27. L Las soluciones de Frobenius de la ecuación del Ejercicio 22 se definen en (0, ρ), donde ρ se define en el teorema 9.7.5.2. Encuentre ρ y realice los experimentos (a), (b) y (c) del ejercicio 11 para cada solución de Frobenius, con M = 20 y δ = 0.25ρ, 0.5ρ y 0.75ρ en el procedimiento de verificación descrito al final de esta sección.

      En los ejercicios 28 a 32 encuentre un conjunto fundamental de soluciones de Frobenius. Calcule los coeficientes a₀, . . . , a_N para N al menos 7 en cada solución.

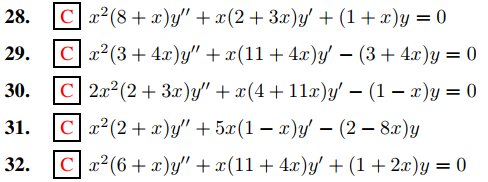
      En los Ejercicios 33 a 46 encuentre un conjunto fundamental de soluciones de Frobenius. Dé fórmulas explícitas para los coeficientes en cada solución.

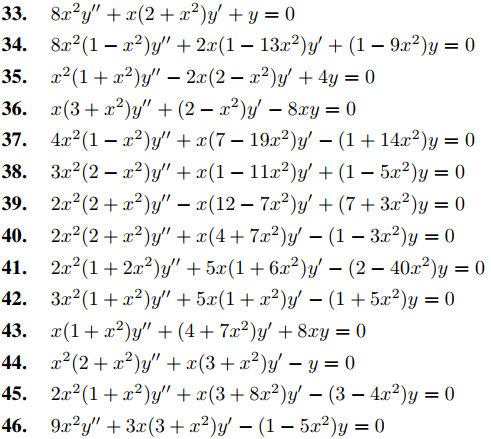
      En los Ejercicios 47 a 51 encuentre un conjunto fundamental de soluciones de Frobenius. Calcule los coeficientes a0, . . . , a_2M para M al menos 7 en cada solución.

52. Suponga que r₁ > r₂, a₀ = b₀ = 1, y la serie de Frobenius

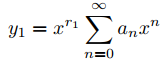  y 

ambos convergen en un intervalo (0, ρ).

(a) Demuestre que y₁ e y₂ son linealmente independientes en (0, ρ). AYUDA: Demuestre que si c₁ y c₂ son constantes tales que c₁y₁ + c₂y₂ ≡ 0 en (0, ρ), entonces

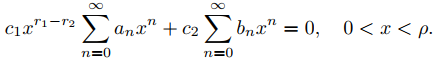
Entonces sea x → 0+ para concluir que c₂ = 0.

(b) Use el resultado de (a) para completar la prueba del Teorema 9.7.5.3.

53. La ecuación

x²y′′ + xy′ + (x² − v²)y = 0         (A)

es la ecuación de Bessel de orden ν. (Aquí ν es un parámetro, y este uso de “orden” no debe confundirse con su uso habitual como “el orden de la ecuación”.) Las soluciones de (A) son funciones de Bessel de orden ν.

(a) Suponiendo que ν no es un número entero, encuentre un conjunto fundamental de soluciones de Frobenius de (A).
(b) Si ν = 1/2, las soluciones de (A) se reducen a funciones elementales familiares. Identifica estas funciones.

54. (a) Verifique que

  y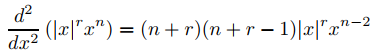 

si x ≠ 0.

(b) Sea

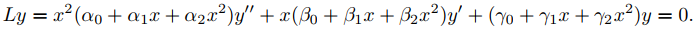
Muestre que si 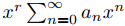es una solución de L_y = 0 en (0, ρ) entonces es una solución en (−ρ, 0) y (0, ρ) .

55. (a) Deduzca de la ecuación (9.7.5.20) que

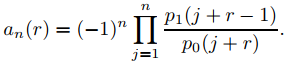
(b) Concluya que si p₀(r) = α₀(r − r₁)(r − r₂) donde r₁ − r₂ no es un número entero, entonces

  y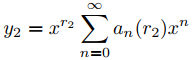 

forman un conjunto fundamental de soluciones de Frobenius de

(c) Demuestre que si p₀ satisface las hipótesis de (b) entonces

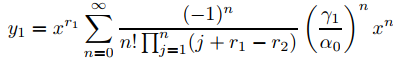
y

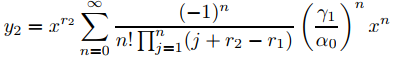
forman un conjunto fundamental de soluciones de Frobenius de

α₀x²y′′ + β₀xy′ + (γ₀ + γ₁x)y = 0.

56. Sea

L_y = x²(α₀ + α₂x²y′′ + x(β₀ + β₂x²y′ + (γ₀ + γ₂x²)y = 0

y definir

p₀(r) = α₀r(r − 1) + β₀r + γ₀   y   p₂(r) = α₂r(r − 1) + β₂r + γ₂.

(a) Use el Teorema 9.7.5.2 para demostrar que si

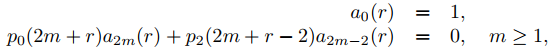       (A)

entonces la serie de Frobenius satisface L_y(x, r) = p₀(r)x^r.

(b) Deduzca de (A) que si p₀(2m + r) es distinto de cero para todo entero positivo

(c) Concluya que si p₀(r) = α₀(r − r₁)(r − r₂) donde r₁ − r₂ no es un entero par, entonces

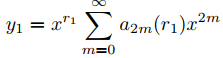  y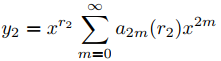 

forman un conjunto fundamental de soluciones de Frobenius de L_y = 0.

(d) Muestre que si p₀ satisface las hipótesis de (c) entonces

y

forman un conjunto fundamental de soluciones de Frobenius de

α₀x²y′′ + β₀xy′ + (γ₀ + γ_2x²)y = 0.

57. Sea

L_y = x²q₀(x)y′′ + xq₁(x)y′ + q₂(x)y,

donde

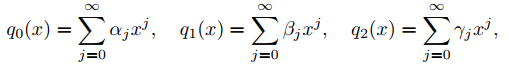
y definir

p_j(r) = α_jr(r − 1) + β_jr + γ_j,  j = 0, 1, . . ..

Sea Muestre que

donde

58. (a) Sea L como en el Ejercicio 57. Demuestre que si

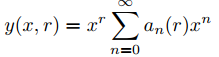
donde

entonces

L_y(x, r) = p₀(r)x^r.

(b) Concluya que si

p₀(r) = α₀(r − r₁)(r − r₂)

donde r₁ − r₂ no es un número entero, entonces y₁ = y(x, r₁) y y₂ = y(x, r₂) son soluciones de L_y = 0.

59. Sea

L_y = x²(α₀ + α_qx^q)y′′ + x(β₀ + β_qx^q)y′ + (γ₀ + γ_qx^q)y

donde q es un entero positivo, y define

p₀(r) = α₀r(r − 1) + β₀r + γ₀   y   p_q(r) = α_qr(r − 1) + β_qr + γ_q.

(a) Demuestre que si

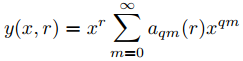
donde

        (A)

entonces

L_y(x, r) = p₀(r)x^r.

(b) Deducir de (A) que

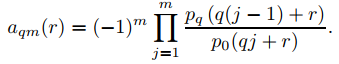
(c) Concluya que si p₀(r) = α₀(r − r₁)(r − r₂) donde r₁ − r₂ no es un múltiplo entero de q, entonces

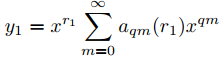  y 

forman un conjunto fundamental de soluciones de Frobenius de L_y = 0.

(d) Demuestre que si p₀ satisface las hipótesis de (c) entonces

y

forman un conjunto fundamental de soluciones de Frobenius de

α₀x²y′′ + β₀xy′ + (γ₀ + γ_qx^q)y = 0.

60. (a) Suponga que α₀, α₁ y α₂ son números reales con α₀ ≠ 0, y está definido por

α0a₁ + α₁a₀ = 0

y

α₀a_n + α₁a_{n − 1} + α₂a_{n − 2} = 0,  n ≥ 2.

Muestre que

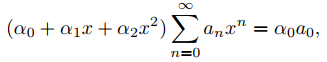
e inferir que

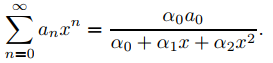
(b) Con α₀, α₁ y α₂ como en (a), considere la ecuación

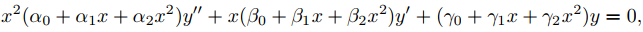       (A)

y defina

Suponga

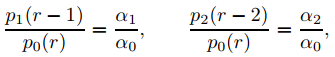
y

p₀(r) = α₀(r − r₁)(r − r₂),

donde r₁ > r₂. Muestre que

  y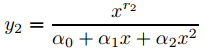 

forman un conjunto fundamental de soluciones de Frobenius de (A) en cualquier intervalo (0, ρ) en el que α₀ + α₁x + α₂x² no tiene ceros.

      En los Ejercicios 61 a 68 use el método sugerido por el Ejercicio 60 para encontrar la solución general en algún intervalo (0, ρ)