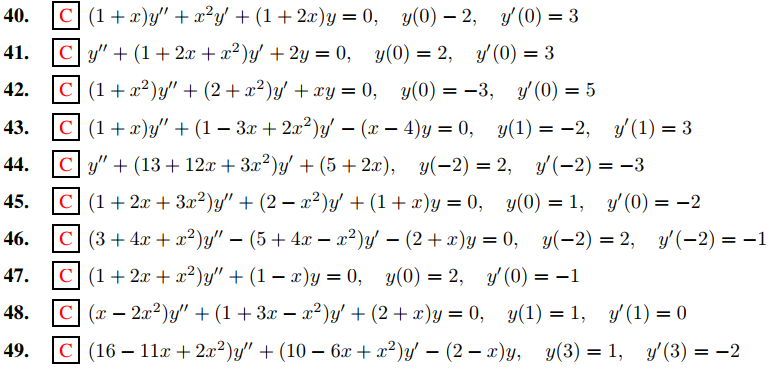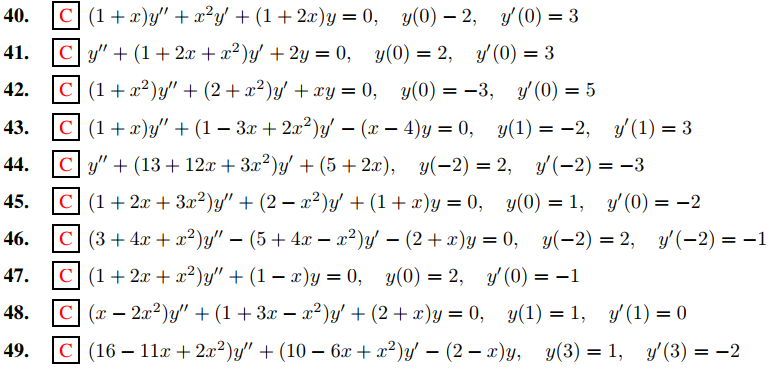| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.2. Soluciones en serie cerca de un punto ordinario II |
Ejercicios propuestos para el Capitulo 9.7.3
En los ejercicios 1 a 12, encuentre los coeficientes a0,. . . , aN para N al menos 7 en la solución en serie 
del problema de valor inicial.
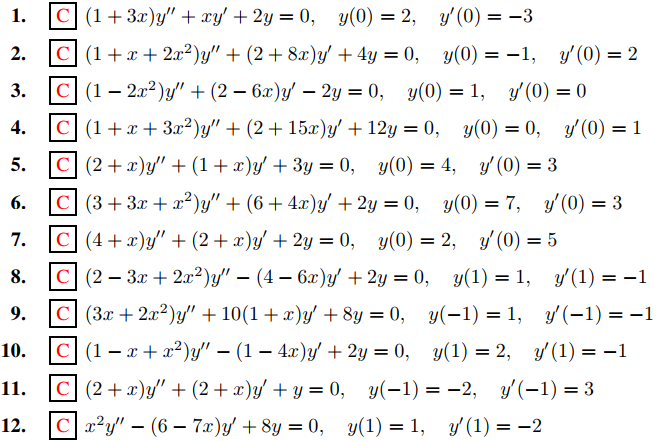
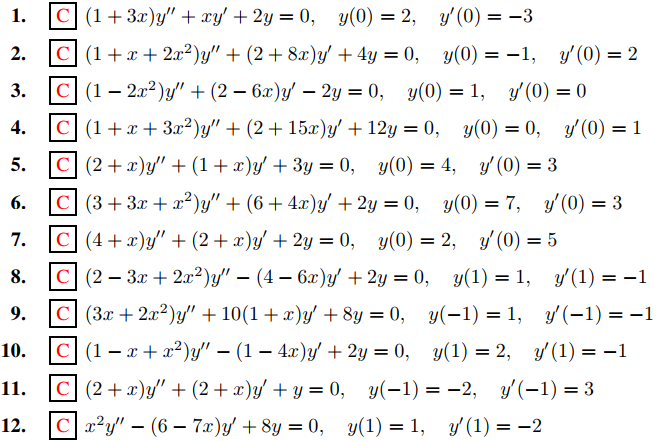
13. L Haz el siguiente experimento para varias opciones de números reales a0, a1 y r, con 0 < r < 1/√2.
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(A)
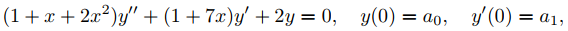
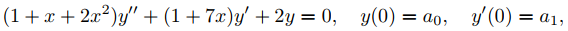
numéricamente en (−r, r). (Vea el Ejemplo 9.7.3.1.)
(b) Para N = 2, 3, 4, . . . , calcule a2, . . . , aN en la solución en serie de potencias 
de (A), y la gráfica
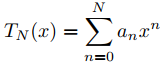
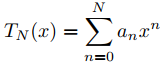
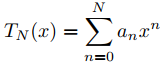
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos.
14. L Haz el siguiente experimento para varias opciones de números reales a0, a1 y r, con 0 < r < 2.
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(A)
numéricamente en (−1 − r, −1 + r). (Consulte el Ejemplo 9.7.3.2. ¿Por qué este intervalo?)
(b) Para N = 2, 3, 4, …, calcule a2, . . ., aN en la solución en serie de potencias
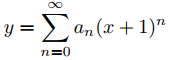
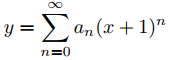
de (A), y la gráfica
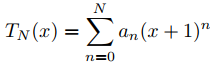
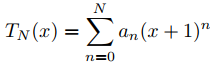
y la solución obtenida en (a) en (−1 − r, −1 + r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos.
15. L Haz el siguiente experimento para varias opciones de a0, a1 y r, con r > 0.
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(A)
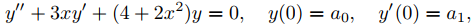
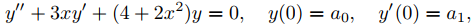
numéricamente en (−r, r). (Vea el Ejemplo 9.7.3.3.)
(b) Encuentre los coeficientes a0, a1, …, aN en la solución en serie de potencias de (A), y la gráfica
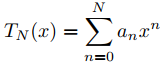
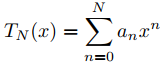
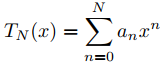
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos.
16. L Haz el siguiente experimento para varias opciones de a0 y a1.
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(1 − x)y′′ − (2 − x)y′ + y = 0, y(0) = a0, y′(0) = a1, (A)
numéricamente en (−r, r).
(b) Encuentre los coeficientes a0, a1, . . . , aN en la solución en serie de potencias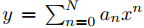 
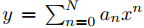
de (A), y grafique
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos. ¿Qué sucede cuando dejas que r → 1?
17. L Siga las instrucciones del Ejercicio 16 para el problema de valor inicial
(1 + x)y′′ + 3y′ + 32y = 0, y(0) = a0, y′(0) = a1.
18. L Siga las instrucciones del Ejercicio 16 para el problema de valor inicial
(1 + x2)y′′ + y′ + 2y = 0, y(0) = a0, y′(0) = a1.
En los Ejercicios 19 a 28 encuentre los coeficientes a0, . . . , aN para N al menos 7 en la solución en serie
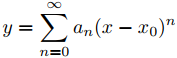
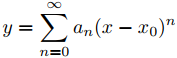
del problema de valor inicial. Tome x0 como el punto donde se imponen las condiciones iniciales.
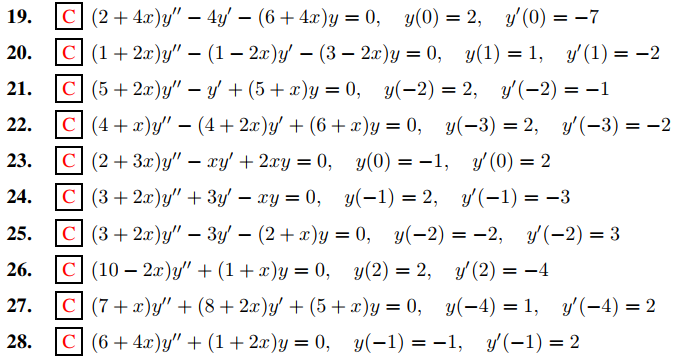
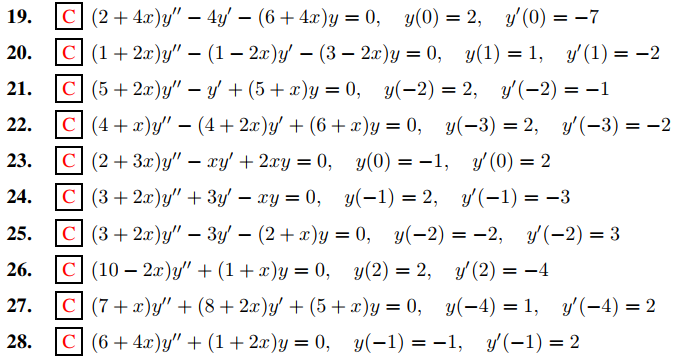
29. Muestre que los coeficientes en la serie de potencias en x para la solución general de
(1 + αx + βx2)y′′ + (γ + δx)y′ + εy = 0
satisface la relación de recurrencia
30. (a) Sean constantes α y β, con β ≠ 0. Demuestre que 
es una solución de
(1 + αx + βx2)y′′ + (2α + 4βx)y′ + 2βy = 0 (A)
si y solo si
an + 2 + αan + 1 + βan = 0, n ≥ 0. (B)
Una ecuación de esta forma se denomina ecuación diferencial lineal homogénea de segundo orden. El polinomio p(r) = r2 + αr + β se denomina polinomio característico de (B). Si r1 y r2 son los ceros de p, entonces 1/r1 y 1/r2 son los ceros de
P0(x) = 1 + αx + βx2.
(b) Suponga que p(r) = (r − r1)(r − r2) donde r1 y r2 son reales y distintos, y sea ρ el menor de los dos números {1/|r1|, 1/|r2| }. Muestre que si c1 y c2 son constantes entonces la sucesión
satisface (B). Concluya de esto que cualquier función de la forma
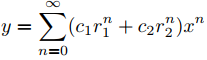
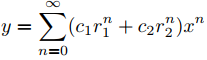
es una solución de (A) en (−ρ, ρ).
(c) Use (b) y la fórmula para la suma de una serie geométrica para mostrar que las funciones
y 
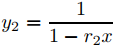
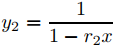
forman un conjunto fundamental de soluciones de (A) en (−ρ, ρ).
(d) Demuestre que {y1, y2} es un conjunto fundamental de soluciones de (A) en cualquier intervalo que no contenga ni 1/r1 ni 1/r2.
(e) Suponga que p(r) = (r − r1)2, y sea ρ = 1/|r1|. Muestre que si c1 y c2 son constantes entonces la sucesión
satisface (B). Concluya de esto que cualquier función de la forma
es una solución de (A) en (−ρ, ρ).
(f) Use (e) y la fórmula para la suma de una serie geométrica para mostrar que las funciones
y 
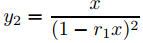
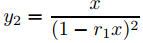
forman un conjunto fundamental de soluciones de (A) en (−ρ, ρ).
(g) Demuestre que {y1, y2} es un conjunto fundamental de soluciones de (A) en cualquier intervalo que no contenga 1/r1.
31. Usa los resultados del Ejercicio 30 para encontrar la solución general de la ecuación dada en cualquier intervalo en el que el polinomio multiplicando y′′ no tenga ceros.
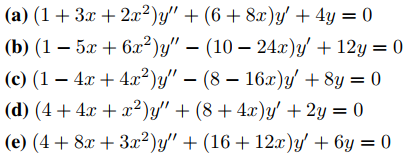
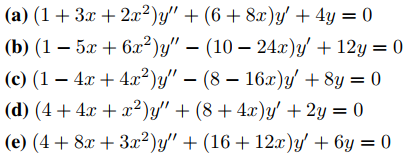
En los Ejercicios 32 a 38 encuentre los coeficientes a0, . . . , aN para N al menos 7 en la solución en serie 
del problema de valor inicial.
39. Encuentra series de potencias en x para las soluciones y1 e y2 de
y′′ + 4xy′ + (2 + 4x2)y = 0
tal que y1(0) = 1, y1′(0) = 0, y2(0) = 0, y2′(0) = 1, e identifique y1 e y2 en términos de funciones elementales familiares.
En los Ejercicios 40 a 49 encuentre los coeficientes a0, …, aN para N al menos 7 en la solución en serie
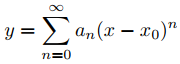
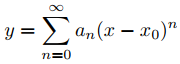
del problema de valor inicial. Tome x0 como el punto donde se imponen las condiciones iniciales.
