| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | Ejercicios propuestos del Capítulo 9.7.2 |
9.7.2 Soluciones en serie cerca de un punto ordinario I
Muchas aplicaciones físicas dan lugar a ecuaciones diferenciales lineales homogéneas de segundo orden de la forma
P0(x)y′′ + P1(x)y′ + P2(x)y = 0, (9.7.2.1)
donde P0, P1 y P2 son polinomios. Por lo general, las soluciones de estas ecuaciones no se pueden expresar en términos de funciones elementales familiares. Por lo tanto, consideraremos el problema de representar soluciones de (9.7.2.1) con series de potencias.
Asumimos en todo momento que P0, P1 y P2 no tienen factores comunes. Entonces decimos que x0 es un punto ordinario de (9.7.2.1) si P0(x0) ≠ 0, o un punto singular si P0(x0) = 0. Para la ecuación de Legendre,
(1 − x2)y′′ − 2xy′ + α(α + 1)y = 0, (9.7.2.2)
x0 = 1 y x0 = −1 son puntos singulares y todos los demás puntos son puntos ordinarios. Para la ecuación de Bessel,
x2y′′ + xy′ + (x2 − ν2) y = 0,
x0 = 0 es un punto singular y todos los demás puntos son puntos ordinarios. Si P0 es una constante distinta de cero como en la ecuación de Airy,
y′′ − xy = 0, (9.7.2.3)
entonces todo punto es un punto ordinario.
Dado que los polinomios son continuos en todas partes, P1/P0 y P2/P0 son continuos en cualquier punto x0 que no sea un cero de P0. Por lo tanto, si x0 es un punto ordinario de (9.7.2.1) y a0 y a1 son números reales arbitrarios, entonces el problema de valor inicial
P0(x)y′′ + P1(x)y′ + P1(x)y = 0, y(x0) = a0, y′(x0) = a1 (9.7.2.4)
tiene una solución única en el intervalo abierto más grande que contiene a x0 y no contiene ceros de P0. Para ver esto, reescribimos la ecuación diferencial en (9.7.2.4) como

y aplicamos el Teorema 9.5.1.1 con p = P1/P0 y q = P2/P0. En esta sección y en la siguiente consideramos el problema de representar soluciones de (9.7.2.1) mediante series de potencias que convergen para valores de x cerca de un punto ordinario x0.
Enunciamos el siguiente teorema sin demostración.
Teorema 9.7.2.1
Supongamos que P0, P1 y P2 son polinomios sin factor común y P0 no es idénticamente igual a cero. Sea x0 un punto tal que P0(x0) ≠ 0, y sea ρ la distancia de x0 al cero más cercano de P0 en el plano complejo. (Si P0 es constante, entonces ρ = ∞). Entonces cada solución de
P0(x)y′′ + P1(x)y′ + P2(x)y = 0 (9.7.2.5)
se puede representar mediante una serie de potencias
 (9.7.2.6)
(9.7.2.6)
que converge al menos en el intervalo abierto (x0 − ρ, x0 + ρ). (Si P0 no es constante, por lo que ρ es necesariamente finito, entonces el intervalo abierto de convergencia de (9.7.2.6) puede ser mayor que (x0 − ρ, x0 + ρ). Si P0 es constante, entonces ρ = ∞ y (x0 − ρ, x0 + ρ) = (−∞, ∞). ♦
Llamamos a (9.7.2.6) una solución en serie de potencias en x − x0 de (9.7.2.5). Ahora desarrollaremos un método para encontrar soluciones en serie de potencias de (9.7.2.5). Para este propósito escribimos (9.7.2.5) como Ly = 0, donde
Ly = P0y′′ + P1y′ + P2y. (9.7.2.7)
El Teorema 9.7.2.1 implica que toda solución de Ly = 0 en (x0 − ρ, x0 + ρ) se puede escribir como

Haciendo x = x0 en esta serie y en la serie

se obtiene y(x0) = a0 y y′(x0) = a1. Dado que cada problema de valor inicial (9.7.2.4) tiene una solución única, esto significa que a0 y a1 pueden elegirse arbitrariamente, y a2, a3, . . . se determinan de manera única a partir de ellas.
Para encontrar a2, a3, . . , escribimos P0, P1 y P2 en potencias de x − x0, sustituimos

en (9.7.2.7), y al agrupar los coeficientes de potencias semejantes de x − x0, da como resultado
 (9.7.2.8)
(9.7.2.8)
donde {b0, b1, . . ., bn, . . .} se expresan en términos de {a0, a1, . . ., an, . . .} y los coeficientes P0, P1 y P2, escritos en potencias de x − x0. Dado que (9.7.2.8) y el inciso (a) del Teorema 9.7.1.5 implican que Ly = 0 si y solo si bn = 0 para n ≥ 0, todas las soluciones en serie de potencias en x − x0 de Ly = 0 se pueden obtener eligiendo a0 y a1 arbitrariamente y calculando a2, a3, . . . , sucesivamente de manera que bn = 0 para n ≥ 0. Por simplicidad, a la serie de potencias así obtenida la llamaremos serie de potencias en x − x0 para la solución general de Ly = 0, sin identificar explícitamente el intervalo abierto de convergencia de la serie .
Ejemplo 9.7.2.1: Representación en series de potencias de la solución general de una ecuación diferencial de segundo orden
Sea x0 un número real arbitrario. Encuentre la serie de potencias en x − x0 para la solución general de
Solución:
Aquí
Ly = y′′ + y.
Si

entonces
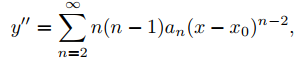
así que

Para agrupar coeficientes de potencias iguales de x − x0, cambiamos el índice de suma en la primera suma. Esto produce

con
bn = (n + 2)(n + 1)an + 2 + an.
Por lo tanto Ly = 0 si y solo si
 (9.7.2.10)
(9.7.2.10)
donde a0 y a1 son arbitrarios. Como los índices de los lados izquierdo y derecho de (9.7.2.10) difieren en dos, escribimos (9.7.2.10) por separado para n par (n = 2m) y n impar (n = 2m + 1). Esto produce
$$ a_{2m+2} = \frac{-a_{2m}}{(2m+2)(2m+1)}, \quad m \geq 0. \tag{9.7.2.11} $$ $$ a_{2m+3} = \frac{-a_{2m+1}}{(2m+3)(2m+2)}, \quad m \geq 0. \tag{9.7.2.12} $$Calculando los coeficientes de las potencias pares de \(x – x_0\) a partir de (9.7.2.11), se obtiene:
$$ a_{2} = -\frac{a_0}{2 \cdot 1}, $$ $$ a_{4} = -\frac{a_{2}}{4 \cdot 3} = -\frac{1}{4 \cdot 3}\left(-\frac{a_0}{2 \cdot 1}\right) = \frac{a_0}{4 \cdot 3 \cdot 2 \cdot 1}, $$ $$ a_{6} = -\frac{a_{4}}{6 \cdot 5} = -\frac{1}{6 \cdot 5}\left(\frac{a_0}{4 \cdot 3 \cdot 2 \cdot 1}\right) = -\frac{a_0}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}, $$y, en general,
$$ a_{2m} = (-1)^m \frac{a_0}{(2m)!}, \quad m \geq 0. \tag{9.7.2.13} $$Calculando los coeficientes de las potencias impares de \( x – x_0 \) a partir de (9.7.2.12) se obtiene:
$$ a_{3} = -\frac{a_{1}}{3 \cdot 2}, $$ $$ a_{5} = -\frac{a_{3}}{5 \cdot 4} = -\frac{1}{5 \cdot 4} \left( -\frac{a_{1}}{3 \cdot 2} \right) = \frac{a_{1}}{5 \cdot 4 \cdot 3 \cdot 2}, $$ $$ a_{7} = -\frac{a_{5}}{7 \cdot 6} = -\frac{1}{7 \cdot 6} \left( \frac{a_{1}}{5 \cdot 4 \cdot 3 \cdot 2} \right) = -\frac{a_{1}}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2}, $$y, en general,
$$ a_{2m+1} = (-1)^m \frac{a_{1}}{(2m+1)!}, \quad m \geq 0. \tag{9.7.2.14} $$Por lo tanto, la solución general de (9.7.2.9) puede escribirse como:
$$ y = \sum_{m=0}^{\infty} a_{2m} (x – x_0)^{2m} + \sum_{m=0}^{\infty} a_{2m+1} (x – x_0)^{2m+1}, $$o, a partir de (9.7.2.13) y (9.7.2.14), como:
$$ y = a_0 \sum_{m=0}^{\infty} (-1)^m \frac{(x – x_0)^{2m}}{(2m)!} + a_1 \sum_{m=0}^{\infty} (-1)^m \frac{(x – x_0)^{2m+1}}{(2m+1)!}. \tag{9,7.2.15} $$Si recordamos del cálculo que
$$ \sum_{m=0}^{\infty} (-1)^m \frac{(x – x_0)^{2m}}{(2m)!} = \cos(x – x_0) \quad \text{y} \quad \sum_{m=0}^{\infty} (-1)^m \frac{(x – x_0)^{2m+1}}{(2m+1)!} = \sin(x – x_0), $$entonces (9.7.2.15) se convierte en
$$ y = a_0 \cos(x – x_0) + a_1 \sin(x – x_0), $$lo cual debería ser familiar.
♦Las ecuaciones como (9.7.2.10), (9.7.2.11) y (9.7.2.12), que definen un coeficiente dado en la sucesión \( \{a_n\} \) en términos de uno o más coeficientes con índices menores, se llaman relaciones de recurrencia. Cuando usamos una relación de recurrencia para calcular los términos de una sucesión, estamos calculando los términos recursivamente.
En el resto de esta sección consideraremos el problema de encontrar soluciones en serie de potencias en \(x – x_0\) para ecuaciones de la forma:
\[ (1 + \alpha (x – x_0)^2 ) y” + \beta (x – x_0)y’ + \gamma y = 0. \tag{9.7.2.16} \]Muchas ecuaciones importantes que aparecen en aplicaciones son de esta forma con \( x_0 = 0 \), incluyendo:
Ecuación de Chebyshev:
\[ (1 – x^2)y” – xy’ + \alpha^2 y = 0. \]Ecuación de Hermite:
\[ y” – 2xy’ + 2\alpha y = 0. \]Dado que \( P_0(x) = 1 + \alpha (x – x_0)^2 \) en (9.7.2.16), el punto \( x_0 \) es un punto ordinario de (9.7.2.16), y el Teorema 9.7.2.1 implica que las soluciones de (9.7.2.16) pueden escribirse como series de potencias en \(x – x_0\) que convergen en el intervalo:
\[ (x_0 – 1/\sqrt{|\alpha|},\; x_0 + 1/\sqrt{|\alpha|}) \quad \text{si } \alpha \ne 0, \]o en \( (-\infty, \infty) \) si \( \alpha = 0 \).
Veremos que los coeficientes de estas series de potencias pueden obtenerse por métodos similares al usado en el Ejemplo 9.7.2.1.
Para simplificar el hallazgo de los coeficientes, introducimos una notación para productos:
\[ \prod_{j=r}^{s} b_j = b_r b_{r+1} \cdots b_s \quad \text{si } s \ge r. \]Así,
\[ \prod_{j=2}^{7} b_j = b_2 b_3 b_4 b_5 b_6 b_7, \] \[ \prod_{j=0}^{4} (2j + 1) = (1)(3)(5)(7)(9) = 945, \]y
\[ \prod_{j=2}^{2} j^2 = 2^2 = 4. \]Definimos
\[ \prod_{j=r}^{s} b_j = 1 \quad \text{si } s < r, \]sin importar la forma de \( b_j \).
Ejemplo 9.7.2.2
Encontrar la serie de potencias en \(x\) para la solución general de
\[ (1 + 2x^2)y” + 6xy’ + 2y = 0. \tag{9.7.2.17} \]Solución: Aquí
\[ Ly = (1 + 2x^2)y” + 6xy’ + 2y. \]Si
\[ y = \sum_{n=0}^{\infty} a_n x^n, \]entonces
\[ y’ = \sum_{n=1}^{\infty} n\,a_n x^{n-1} \quad \text{y} \quad y” = \sum_{n=2}^{\infty} n(n-1)a_n x^{n-2}. \]Por lo tanto,
\[ Ly = (1 + 2x^2)\sum_{n=2}^{\infty} n(n-1)a_n x^{n-2} + 6x\sum_{n=1}^{\infty} n a_n x^{n-1} + 2\sum_{n=0}^{\infty} a_n x^{n}. \] \[ = \sum_{n=2}^{\infty} n(n-1)a_n x^{n-2} + \sum_{n=0}^{\infty} [2n(n-1) + 6n + 2]a_n x^{n}. \] \[ = \sum_{n=2}^{\infty} n(n-1)a_n x^{n-2} + 2\sum_{n=0}^{\infty} (n+1)^2 a_n x^{n}. \] Para reunir los coeficientes de \(x^n\), desplazamos el índice de suma en la primera suma. Esto produce \[ Ly = \sum_{n=0}^{\infty} (n+2)(n+1)a_{n+2}x^n + 2\sum_{n=0}^{\infty}(n+1)^2 a_n x^n = \sum_{n=0}^{\infty} b_n x^n, \] donde \[ b_n = (n+2)(n+1)a_{n+2} + 2(n+1)^2 a_n, \qquad n \ge 0. \] Para obtener soluciones de (9.7.2.17), hacemos \( b_n = 0 \) para \( n \ge 0 \). Esto es equivalente a la relación de recurrencia \[ a_{n+2} = -2\,\frac{n+1}{n+2}\, a_n, \qquad n \ge 0. \tag{9.7.2.18} \] Como los índices en el lado izquierdo y derecho difieren en dos, escribimos (9.7.2.18) por separado para \( n = 2m \) y \( n = 2m+1 \), como en el Ejemplo 9.7.2.1. Esto da \[ a_{2m+2} = -2\,\frac{2m+1}{2m+2}a_{2m} = -\frac{2m+1}{m+1}a_{2m}, \qquad m \ge 0. \tag{9.7.2.19} \] y \[ a_{2m+3} = -2\,\frac{2m+2}{2m+3}a_{2m+1} = -4\,\frac{m+1}{2m+3}a_{2m+1}, \qquad m \ge 0. \tag{9.7.2.20} \] Calculando los coeficientes de las potencias pares de \(x\) a partir de (9.7.2.19) se obtiene \[ a_2 = -\frac{1}{1}a_0, \] \[ a_4 = -\frac{3}{2}a_2 = -\frac{3}{2}\left(-\frac{1}{1}\right)a_0 = \frac{1\cdot 3}{1\cdot 2}a_0, \] \[ a_6 = -\frac{5}{3}a_4 = -\frac{5}{3}\cdot \frac{1\cdot 3}{1\cdot 2}a_0 = \frac{1\cdot 3\cdot 5}{1\cdot 2\cdot 3}a_0, \] \[ a_8 = -\frac{7}{4}a_6 = -\frac{7}{4}\cdot\frac{1\cdot 3\cdot 5}{1\cdot 2\cdot 3}a_0 = \frac{1\cdot 3\cdot 5\cdot 7}{1\cdot 2\cdot 3\cdot 4}a_0. \] En general, \[ a_{2m} = (-1)^m \frac{\displaystyle\prod_{j=1}^{m}(2j-1)}{m!}\, a_0, \qquad m \ge 0. \tag{9.7.2.21} \] (Nótese que (9.7.2.21) es correcta para \(m=0\) porque definimos \(\prod_{j=1}^{0} b_j = 1\) para cualquier \(b_j\).)El cálculo de los coeficientes de las potencias impares de $x$ a partir de (9.7.2.20) produce:
\[ a_3 = -\frac{1}{3} a_1, \]
\[ a_5 = -\frac{2}{5} a_3 = -\frac{2}{5} \left(-\frac{1}{3} a_1 \right) = 4^2 \frac{1 \cdot 2}{3 \cdot 5} a_1, \]
\[ a_7 = -\frac{3}{7} a_5 = -\frac{3}{7} \left( 4^2 \frac{1 \cdot 2}{3 \cdot 5} a_1 \right) = -4^3 \frac{1 \cdot 2 \cdot 3}{3 \cdot 5 \cdot 7} a_1, \]
\[ a_9 = -\frac{4}{9} a_7 = -\frac{4}{9} \left( -4^3 \frac{1 \cdot 2 \cdot 3}{3 \cdot 5 \cdot 7} a_1 \right) = 4^4 \frac{1 \cdot 2 \cdot 3 \cdot 4}{3 \cdot 5 \cdot 7 \cdot 9} a_1. \]
En general,
\[ a_{2m+1} = \frac{(-1)^m 4^m m!}{\prod_{j=1}^m (2j+1)} a_1, \quad m \ge 0. \quad (9.7.2.22) \]
A partir de (9.7.2.21) y (9.7.2.22),
\[ y = a_0 \sum_{m=0}^{\infty} (-1)^m \frac{\prod_{j=1}^m (2j-1)}{m!} x^{2m} + a_1 \sum_{m=0}^{\infty} (-1)^m \frac{4^m m!}{\prod_{j=1}^m (2j+1)} x^{2m+1}. \]
es la serie de potencias en $x$ para la solución general de (9.7.2.17). Dado que $P_0(x) = 1+2x^2$ no tiene ceros reales, el Teorema 9.5.5.1 implica que toda solución de (9.7.2.17) está definida en $(-\infty, \infty)$. Sin embargo, dado que $P_0(\pm i / \sqrt{2}) = 0$, el Teorema 9.7.2.1 implica solo que la serie de potencias converge en $(-1/\sqrt{2}, 1/\sqrt{2})$ para cualquier elección de $a_0$ y $a_1$.
♦Los resultados de los Ejemplos 9.7.2.1 y 9.7.2.2 son consecuencias del siguiente teorema general.
Teorema 9.7.2.2
Los coeficientes $\{a_n\}$ en cualquier solución \[ y = \sum_{n=0}^{\infty} a_n (x – x_0)^n \] de \[ (1 + \alpha (x – x_0)^2)y” + \beta (x – x_0)y’ + \gamma y = 0 \tag{9.7.2.23} \] satisfacen la relación de recurrencia \[ a_{n+2} = -\frac{p(n)}{(n+2)(n+1)}\,a_n, \qquad n \ge 0, \tag{9.7.2.24} \] donde \[ p(n) = \alpha n(n-1) + \beta n + \gamma. \tag{9.7.2.25} \] Además, los coeficientes de las potencias pares e impares de \(x – x_0\) pueden calcularse por separado como \[ a_{2m+2} = -\frac{p(2m)}{(2m+2)(2m+1)}\,a_{2m}, \qquad m \ge 0, \tag{9.7.2.26} \] y \[ a_{2m+3} = -\frac{p(2m+1)}{(2m+3)(2m+2)}\,a_{2m+1}, \qquad m \ge 0, \tag{9.7.2.27} \] donde \(a_0\) y \(a_1\) son arbitrarios. ♦Demostración:
Aquí \[ Ly = (1 + \alpha (x – x_0)^2) y” + \beta (x – x_0) y’ + \gamma y. \] Si \[ y = \sum_{n=0}^{\infty} a_n (x – x_0)^n, \] entonces \[ y’ = \sum_{n=1}^{\infty} n a_n (x – x_0)^{n-1} \quad \text{y} \quad y” = \sum_{n=2}^{\infty} n(n-1) a_n (x – x_0)^{n-2}. \] Por lo tanto, \[ Ly = \sum_{n=2}^{\infty} n(n-1) a_n (x – x_0)^{n-2} \;+\; \sum_{n=0}^{\infty} [\alpha n(n-1) + \beta n + \gamma] a_n (x – x_0)^n \] \[ =\; \sum_{n=2}^{\infty} n(n-1) a_n (x – x_0)^{n-2} \;+\; \sum_{n=0}^{\infty} p(n) a_n (x – x_0)^n, \] de (9.7.2.25). Para reunir los coeficientes de las potencias de \(x – x_0\), desplazamos el índice de suma en la primera suma. Esto da \[ Ly = \sum_{n=0}^{\infty} \big[(n+2)(n+1) a_{n+2} + p(n) a_n \big] (x – x_0)^n. \] Así, \(Ly = 0\) si y solo si \[ (n+2)(n+1) a_{n+2} + p(n) a_n = 0, \qquad n \ge 0, \] lo cual es equivalente a (9.7.2.24). Escribiendo (9.7.2.24) por separado para los casos \(n = 2m\) y \(n = 2m+1\), se obtienen (9.7.2.26) y (9.7.2.27). ♦Ejemplo 9.7.2.3
Halle la serie de potencias en \(x – 1\) para la solución general de \[ (2 + 4x – 2x^2)y” – 12(x – 1)y’ – 12y = 0. \tag{9.7.2.28} \]Solución:
Primero debemos escribir el coeficiente \(P_0(x) = 2 + 4x – x^2\) en potencias de \(x – 1\). Para hacerlo, escribimos \(x = (x – 1) + 1\) en \(P_0(x)\) y luego expandimos los términos, reuniendo potencias de \(x – 1\); así: \[ 2 + 4x – x^2 = 2 + 4[(x – 1) + 1] – 2[(x – 1) + 1]^2 = 4 – 2(x – 1)^2. \] Por lo tanto, podemos reescribir (9.7.2.28) como \[ (4 – 2(x – 1)^2)y” – 12(x – 1)y’ – 12y = 0, \] o equivalentemente, \[ \left(1 – \frac{1}{2}(x – 1)^2\right)y” – 3(x – 1)y’ – 3y = 0. \] Esto es de la forma (9.7.2.23) con \(\alpha = -\frac{1}{2}\), \(\beta = -3\), y \(\gamma = -3\). Por lo tanto, de (9.7.2.25) \[ p(n) = \frac{n(n-1)}{2} – 3n – 3 = -\frac{(n+2)(n+3)}{2}. \] Así, el Teorema 9.5.5.2 implica que \[ a_{2m+2} = -\frac{p(2m)}{(2m+2)(2m+1)}a_{2m} = \frac{(2m+2)(2m+3)}{2(2m+2)(2m+1)}a_{2m} = \frac{2m+3}{2(2m+1)}a_{2m}, \quad m \ge 0, \] y \[ a_{2m+3} = -\frac{p(2m+1)}{(2m+3)(2m+2)}a_{2m+1} = \frac{(2m+3)(2m+4)}{2(2m+3)(2m+2)}a_{2m+1} = \frac{m+2}{2(m+1)}a_{2m+1}, \quad m \ge 0. \] Se deja al lector mostrar que \[ a_{2m} = \frac{2m + 1}{2^m}a_0 \quad \text{y} \quad a_{2m+1} = \frac{m + 1}{2^m}a_1, \quad m \ge 0, \] lo cual implica que la serie de potencias en \(x – 1\) para la solución general de (9.7.2.28) es \[ y = a_0 \sum_{m=0}^{\infty} \frac{2m + 1}{2^m}(x – 1)^{2m} \;+\; a_1 \sum_{m=0}^{\infty} \frac{m + 1}{2^m}(x – 1)^{2m+1}. \] ♦En los ejemplos considerados hasta ahora, pudimos obtener fórmulas cerradas para los coeficientes de las soluciones en serie de potencias. En algunos casos, esto es imposible y debemos conformarnos con calcular un número finito de términos de la serie. El siguiente ejemplo ilustra esto con un problema de valor inicial.
Ejemplo 9.7.2.4
Calcule \(a_0,a_1,\dots,a_7\) en la solución en serie \(y=\sum_{n=0}^{\infty} a_n x^n\) del problema de valor inicial \[ (1 + 2x^2) y” + 10x y’ + 8y = 0,\qquad y(0)=2,\qquad y'(0)=-3. \tag{9.7.2.29} \]Solución: Como \(\alpha = 2\), \(\beta = 10\), y \(\gamma = 8\) en (9.7.2.29),
\[ p(n) = 2n(n-1) + 10n + 8 = 2(n+2)^2. \]Por lo tanto,
\[ a_{n+2} = -2 \frac{(n+2)^2}{(n+2)(n+1)} a_n = -2 \frac{n+2}{n+1} a_n, \qquad n \ge 0. \]Escribiendo esta ecuación por separado para \(n = 2m\) y \(n = 2m+1\) obtenemos
\[ a_{2m+2} = -2 \frac{(2m+2)}{2m+1} a_{2m} = -4 \frac{m+1}{2m+1} a_{2m}, \qquad m \ge 0. \tag{9.7.2.30} \] \[ a_{2m+3} = -2 \frac{(2m+3)}{2m+2} a_{2m+1} = \frac{2m+3}{m+1} a_{2m+1}, \qquad m \ge 0. \tag{9.7.2.31} \]Comenzando con \(a_0 = y(0) = 2\), calculamos \(a_2\), \(a_4\) y \(a_6\) usando (9.7.2.30):
\[ a_2 = -4 \frac{1}{1} \,2 = -8, \] \[ a_4 = -4 \frac{2}{3}(-8) = \frac{64}{3}, \] \[ a_6 = -4 \frac{3}{5}\left(\frac{64}{3}\right) = -\frac{256}{5}. \]Comenzando con \(a_1 = y'(0) = -3\), calculamos \(a_3\), \(a_5\) y \(a_7\) usando (9.7.2.31):
\[ a_3 = -\frac{3}{1}(-3) = 9, \] \[ a_5 = -\frac{5}{2} \,9 = -\frac{45}{2}, \] \[ a_7 = -\frac{7}{3}\left(-\frac{45}{2}\right) = \frac{105}{2}. \]Por lo tanto, la solución de (9.7.2.29) es
\[ y = 2 – 3x – 8x^2 + 9x^3 + \frac{64}{3}x^4 – \frac{45}{2}x^5 – \frac{256}{5}x^6 + \frac{105}{2}x^7 + \cdots. \] ♦USO DE LA TECNOLOGÍA
Calcular coeficientes recursivamente como en el Ejemplo 9.7.2.4, es tedioso. Recomendamos que realices este tipo de cómputo escribiendo un pequeño programa que implemente la relación de recurrencia correspondiente en una calculadora o en una computadora. Puede que quieras hacer esto para verificar ejemplos y para realizar ejercicios (identificados con el símbolo C) en este capítulo que requieren el cálculo numérico de los coeficientes en soluciones en series. Nosotros obtuvimos las respuestas a estos ejercicios utilizando software capaz de producir respuestas en forma de números racionales. Sin embargo, es perfectamente aceptable —y más práctico— obtener tus respuestas en forma decimal. Siempre puedes verificarlas convirtiendo nuestras fracciones a decimales.
Si estás interesado en usar realmente series para calcular aproximaciones numéricas de soluciones de una ecuación diferencial, entonces el que exista o no una fórmula cerrada simple para los coeficientes es esencialmente irrelevante. Para propósitos computacionales es normalmente más eficiente comenzar con los coeficientes dados \(a_0 = y(x_0)\) y \(a_1 = y'(x_0)\), calcular \(a_2, a_3, \ldots, a_N\) recursivamente, y después calcular valores aproximados de la solución a partir del polinomio de Taylor
\[ T_N(x) = \sum_{n=0}^{N} a_n (x – x_0)^n. \]
El punto clave es decidir cómo escoger \(N\) de forma que la aproximación \(y(x) \approx T_N(x)\) sea suficientemente precisa en el subintervalo del intervalo de convergencia que te interesa. En los ejercicios computacionales de esta y las siguientes dos secciones, a menudo se te pedirá obtener la solución de un problema dado mediante integración numérica con un software de tu elección (ver en la Sección 9.10.1, para una discusión breve de uno de estos métodos), y comparar la solución obtenida de este modo con las aproximaciones obtenidas con \(T_N\) para varios valores de \(N\). Este es un tipo típico de ejercicio de libro, diseñado para darte una idea de cómo se comporta la precisión de la aproximación \(y(x) \approx T_N(x)\) en función de \(N\) y del intervalo que estás estudiando. En la vida real, uno elegiría uno u otro de estos métodos (integración numérica o solución en serie).
Si decides usar el método de solución en series, entonces un procedimiento práctico para determinar un valor adecuado de \(N\) consiste en incrementar \(N\) hasta que el máximo de \(|T_N – T_{N-1}|\) en el intervalo de interés esté dentro del margen de error que estás dispuesto a aceptar.
Al realizar problemas computacionales que requieren soluciones numéricas de ecuaciones diferenciales, debes elegir el procedimiento de integración numérica más preciso que soporte tu software y experimentar con el tamaño del paso hasta estar seguro de que los resultados numéricos son suficientemente precisos para el problema en cuestión.
