| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | 9.7.2. Soluciones en serie cerca de un punto ordinario I |
Ejercicios propuestos para el Capítulo 9.7.2
En los ejercicios 1 a 8, encuentre la serie de potencias en x para la solución general.
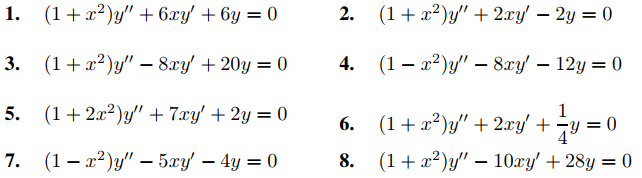
9. L
(a) Encuentre la serie de potencias en x para la solución general de y′′ + xy′ + 2y = 0.
(b) Para varias opciones de a0 y a1, use el software de ecuaciones diferenciales para resolver el problema de valor inicial
y′′ + xy′ + 2y = 0, y(0) = a0, y′(0) = a1, (A)
(c) Para r fija en el gráfico {1, 2, 3, 4, 5}
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos.
10. L Siga las instrucciones del Ejercicio 9 para la ecuación diferencial
y′′ + 2xy′ + 3y = 0.
En los Ejercicios 11 – 13 encuentre a0, . . . , aN para N al menos 7 en la solución en serie de potencias 
del problema de valor inicial.
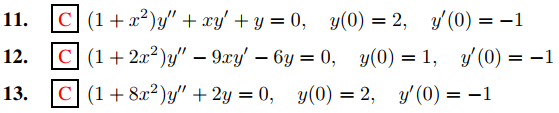
14. L Haz el siguiente experimento para varias opciones de números reales a0, a1 y r, con 0 < r < 1/√2
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(1 − 2x2)y′′ − xy′ + 3y = 0, y(0) = a0, y′(0) = a1, (A)
numéricamente en (−r, r).
(b) Para N = 2, 3, 4, . . . , calcule a2, . . . , aN en la solución en serie de potencias de (A), y la gráfica
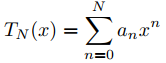
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos.
15. L Haga (a) y (b) para varios valores de r en (0, 1):
(a) Utilice un software de ecuaciones diferenciales para resolver el problema de valor inicial
(1 + x2)y′′ + 10xy′ + 14y = 0, y(0) = 5, y′(0) = 1, (A)
numéricamente en (−r, r).
(b) Para N = 2, 3, 4, . . . , calcule a2, . . . , aN en la solución en serie de potencias de (A) y la gráfica
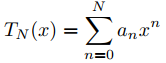
y la solución obtenida en (a) en (−r, r). Continúe aumentando N hasta que no haya una diferencia perceptible entre los dos gráficos. ¿Qué sucede con el N requerido cuando r → 1?
(c) Pruebe (a) y (b) con r = 1.2. Explique sus resultados.
En los ejercicios 16 a 20, encuentre la serie de potencias en x − x0 para la solución general.
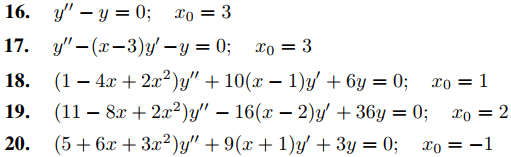
En los Ejercicios 21 a 26 encuentre a0, . . . , aN para N al menos 7 en la serie de potencias 
para la solución del problema de valor inicial. Tome x0 como el punto donde se imponen las condiciones iniciales.
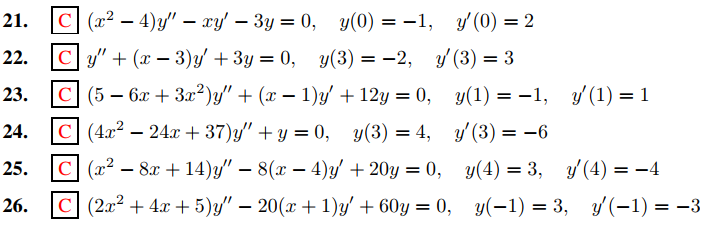
27. (a) Halle una serie de potencias en x para la solución general de
(1 + x2)y′′ + 4xy′ + 2y = 0. (A)
(b) Use (a) y la fórmula
para la suma de una serie geométrica para encontrar una expresión de forma cerrada para la solución general de (A) en (−1, 1).
(c) Demuestre que la expresión obtenida en (b) es en realidad la solución general de de (A) en (−∞, ∞).
28. Utilice el Teorema 9.7.2.2 para demostrar que la serie de potencias en x para la solución general de
(1 + αx2)y′′ + βxy′ + γy = 0
es
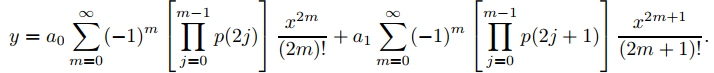
29. Usa el ejercicio 28 para mostrar que todas las soluciones de
(1 + αx2)y′′ + βxy′ + γy = 0
son polinomios si y solo si
αn(n − 1) + βn + γ = α(n − 2r)(n − 2s − 1),
donde r y s son enteros no negativos.
30. (a) Utilice el ejercicio 28 para demostrar que la serie de potencias en x para la solución general de
(1 − x2)y′′ − 2bxy′ + α(α + 2b − 1)y = 0
es y = a0y1 + a1y2, donde
y
(b) Suponga que 2b no es un entero impar negativo y k es un entero no negativo. Demostrar que y1 es un polinomio de grado 2k tal que y1(−x) = y1(x) si α = 2k, mientras que y2 es un polinomio de grado 2k + 1 tal que y2(−x) = −y2(−x) si α = 2k + 1. Concluya que si n es un entero no negativo, entonces existe un polinomio Pn de grado n tal que Pn(−x) = (−1)nPn(x) y
(1 − x2)Pn′′ − 2bxPn′ + n(n + 2b − 1)Pn = 0. (A)
(c) Demuestre que (A) implica que
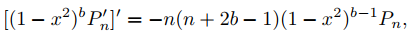
y use esto para mostrar que si m y n son enteros no negativos, entonces
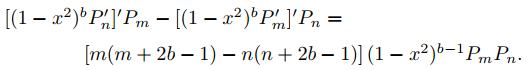(B)
(d) Ahora suponga que b > 0. Use (B) e integración por partes para mostrar que si m ≠ n, entonces
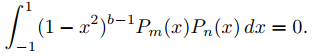
(Decimos que Pm y Pn son ortogonales en (−1, 1) con respecto a la función de ponderación (1 − x2)b − 1.)
31. (a) Utilice el ejercicio 28 para demostrar que la serie de potencias en x para la solución general de la ecuación de Hermite
y′′ − 2xy′ + 2αy = 0
es y = a0y1 + a1y1, donde
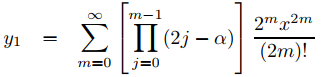
y
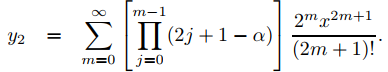
(b) Suponga que k es un entero no negativo. Demostrar que y1 es un polinomio de grado 2k tal que y1(−x) = y1(x) si α = 2k, mientras que y2 es un polinomio de grado 2k + 1 tal que y2(−x) = −y2(−x) si α = 2k + 1. Concluya que si n es un entero no negativo, entonces existe un polinomio Pn de grado n tal que Pn(−x) = (−1)nPn(x) y
Pn′′ − 2xPn′ + 2nPn = 0. (A)
(c) Demuestre que (A) implica que
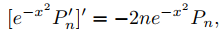
y use esto para mostrar que si m y n son enteros no negativos, entonces
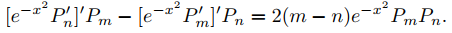(B)
(d) Use (B) e integración por partes para mostrar que si m ≠ n, entonces
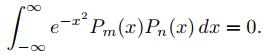
(Decimos que Pm y Pn son ortogonales en (−∞, ∞) con respecto a la función de ponderación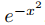 
.)
32. Considera la ecuación
(1 + αx3) y′′ + βx2y′ + γxy = 0, (A)
y sea p(n) = αn(n − 1) + βn + γ. (El caso especial y′′ − xy = 0 de (A) es la ecuación de Airy).
(a) Modifique el argumento utilizado para probar el Teorema 9.7.2.2 para mostrar que
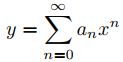
es una solución de (A) si y sólo si a2 = 0 y
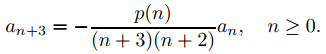
(b) Demuestre a partir de (a) que an = 0 a menos que n = 3m o n = 3m + 1 para algún entero no negativo m, y que
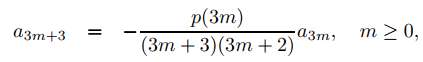
y
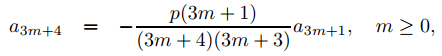
donde a0 y a1 pueden especificarse arbitrariamente.
(c) Concluya de (b) que la serie de potencias en x para la solución general de (A) es
En los Ejercicios 33 a 37 use el método del Ejercicio 32 para encontrar la serie de potencias en x para la solución general.
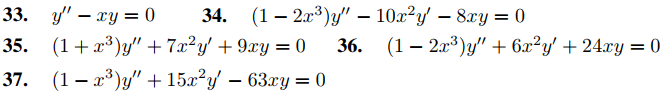
38. Considere la ecuación
(A)
donde k es un entero positivo, y sea p(n) = αn(n − 1) + βn + γ.
(a) Modifique el argumento utilizado para probar el Teorema 9.7.2.2 para mostrar que
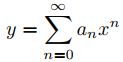
es una solución de (A) si y solo si an = 0 para 2 ≤ n ≤ k + 1 y
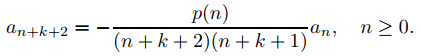
(b) Demuestre a partir de (a) que an = 0 a menos que n = (k + 2)m o n = (k + 2)m + 1 para algún entero no negativo m, y que
y
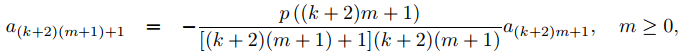
donde a0 y a1 pueden especificarse arbitrariamente.
(c) Concluya de (b) que la serie de potencias en x para la solución general de (A) es
En los ejercicios 39 a 44, use el método del ejercicio 38 para encontrar la serie de potencias en x para la solución general.
