| 9. Ecuaciones diferenciales | 9.4. Aplicaciones de ecuaciones de primer orden | 9.4.3 Mecánica elemental |
Ejercicios propuestos para el Capítulo 9.4.3
Excepto donde se indique lo contrario, suponga que la magnitud de la fuerza gravitacional sobre un objeto con masa m es constante e igual a mg. En ejercicios que involucren movimiento vertical, tome la dirección hacia arriba como positiva.
1. Un bombero que pesa 192 lb se desliza por un poste de fuego infinitamente largo que ejerce una fuerza de resistencia por fricción con una magnitud proporcional a su velocidad, con k = 2.5 lb-s/pie. Suponiendo que parte del reposo, encuentre su velocidad en función del tiempo y encuentre su velocidad terminal.
2. Un bombero que pesa 192 lb se desliza por un poste de fuego infinitamente largo que ejerce una fuerza resistiva de fricción con magnitud proporcional a su velocidad, con constante de proporcionalidad k. Encuentre k, dado que su velocidad terminal es −16 pie/s, y luego encuentre su velocidad v como una función de t. Suponga que parte del reposo.
3. Un bote pesa 64 000 lb. Su hélice produce un empuje constante de 50 000 lb y el agua ejerce una fuerza resistiva de magnitud proporcional a la velocidad, con k = 2000 lb-s/pie. Suponiendo que el bote parte del reposo, encuentre su velocidad en función del tiempo y encuentre su velocidad terminal.
4. Una fuerza horizontal constante de 10 N empuja una masa de 20 kg a través de un medio que resiste su movimiento con 0,5 N por cada m/s de velocidad. La velocidad inicial de la masa es de 7 m/s en dirección opuesta a la dirección de la fuerza aplicada. Encuentre la velocidad de la masa para t > 0.
5. Una piedra que pesa 1/2 lb se lanza hacia arriba desde una altura inicial de 5 pies con una velocidad inicial de 32 pies/s. La resistencia del aire es proporcional a la velocidad, con k = 1/128 lb-s/pie. Encuentre la altura máxima alcanzada por la piedra.
6. Un automóvil de 3200 lb se mueve a 64 pies/s por una pendiente de 30 grados cuando se queda sin combustible. Encuentre su velocidad después de eso si la fricción ejerce una fuerza resistiva con una magnitud proporcional al cuadrado de la velocidad, con k = 1 lb-s2/pie2. Encuentre también su velocidad terminal.
7. Un peso de 96 lb se deja caer desde el reposo en un medio que ejerce una fuerza resistiva de magnitud proporcional a la velocidad. Encuentre su velocidad como una función del tiempo si su velocidad terminal es −128 pie/s.
8. Un objeto con masa m se mueve verticalmente a través de un medio que ejerce una fuerza resistiva con magnitud proporcional a la velocidad. Sea y = y(t) la altitud del objeto en el tiempo t, con y(0) = y0. Utilice los resultados del Ejemplo 9.4.3.1 para demostrar que


9. Un objeto con masa m se lanza verticalmente hacia arriba con velocidad inicial v0 desde la superficie de la Tierra (y0 = 0) en un medio que ejerce una fuerza resistiva con magnitud proporcional a la velocidad. Encuentre el tiempo T cuando el objeto alcanza su altura máxima ym. Luego usa el resultado del Ejercicio 8 para encontrar ym.
10. Un objeto que pesa 256 lb se deja caer desde el reposo en un medio que ejerce una fuerza resistiva de magnitud proporcional al cuadrado de la velocidad. La magnitud de la fuerza de resistencia es 1 lb cuando |v| = 4 pies/seg. Encuentre v para t > 0 y encuentre su velocidad terminal.
11. A un objeto con masa m se le da una velocidad inicial v0 ≤ 0 en un medio que ejerce una fuerza resistiva con magnitud proporcional al cuadrado de la velocidad. Encuentre la velocidad del objeto para t > 0, y encuentre su velocidad terminal.
12. Un objeto con masa m se lanza verticalmente hacia arriba con velocidad inicial v0 en un medio que ejerce una fuerza resistiva con magnitud proporcional al cuadrado de la velocidad.
(a) Encuentre el tiempo T cuando el objeto alcanza su altura máxima.
(b) Use el resultado del Ejercicio 11 para encontrar la velocidad del objeto para t > T.
13. L A un objeto con masa m se le da una velocidad inicial v0 ≤ 0 en un medio que ejerce una fuerza resistiva de la forma a|v|/(1 + |v|), donde a es una constante positiva.
(a) Establezca una ecuación diferencial para la velocidad del objeto.
(b) Usa tu método numérico favorito para resolver la ecuación que encontraste en (a), para convencerte de que hay un número único a0 tal que limt→∞ s(t) = ∞ si a ≤ a0 y limt→∞ s(t )
existe (finito) si a > a0. (Decimos que a0 es el valor de bifurcación de a.) Trate de encontrar a0 y limt→∞ s(t) en el caso donde a > a0. SUGERENCIA: vea el Ejercicio 14.
14. Un objeto de masa m cae en un medio que ejerce una fuerza resistiva f = f (s), donde s = |v| es la velocidad del objeto. Suponga que f (0) = 0 y f es estrictamente creciente y diferenciable en (0, ∞).
(a) Escriba una ecuación diferencial para la velocidad s = s(t) del objeto. Dé por sentado que todas las soluciones de esta ecuación con s(0) ≥ 0 están definidas para todo t > 0 (lo que tiene sentido desde el punto de vista físico).
(b) Demuestre que si lims→∞ f (s) ≤ mg entonces limt→∞ s(t) = ∞.
(c) Demuestre que si lims→∞ f (s)) > mg entonces limt→∞ s(t) = sT (velocidad terminal), donde f (sT ) = mg. SUGERENCIA: Use el Teorema 9.2.3.1.
15. Una masa de 100 g con velocidad inicial v0 ≤ 0 cae en un medio que ejerce una fuerza resistiva proporcional a la cuarta potencia de la velocidad. La resistencia es de 0,1 N si la velocidad es de 3 m/s.
(a) Plantee el problema de valor inicial para la velocidad v de la masa para t > 0.
(b) Utilice el ejercicio 14(c) para determinar la velocidad terminal del objeto.
(c) C Para confirmar su respuesta a (b), use uno de los métodos numéricos estudiados en el Capítulo 9.3
para calcular soluciones aproximadas en [0, 1] (segundos) del problema de valor inicial de (a), con valores iniciales v0 = 0, −2, −4, . . . , −12. Presente sus resultados en forma gráfica similar a la Figura 9.4.3.3.
16. Un objeto de 64 lb con velocidad inicial v0 ≤ 0 cae a través de un fluido denso que ejerce una fuerza de resistencia proporcional a la raíz cuadrada de la velocidad. La resistencia es de 64 lb si la velocidad es de 16 pie/s.
(a) Plantee el problema de valor inicial para la velocidad v de la masa para t > 0.
(b) Utilice el ejercicio 14(c) para determinar la velocidad terminal del objeto.
(c) C Para confirmar su respuesta a (b), use uno de los métodos numéricos estudiados en el Capítulo 9.3 para calcular soluciones aproximadas en [0, 4] (segundos) del problema de valor inicial de (a), con valores iniciales v0 = 0, −5, −10, . . . , −30. Presente sus resultados en forma gráfica similar a la Figura 9.4.3.3.
En los ejercicios 17 a 20, suponga que la fuerza debida a la gravedad viene dada por la ley de gravitación de Newton. Tome la dirección hacia arriba como positiva.
17. Se va a lanzar una sonda espacial desde una estación espacial a 200 millas sobre la Tierra. Determine su velocidad de escape en millas/s. Tome el radio de la Tierra como 3960 millas.
18. Se va a lanzar un vehículo espacial desde la luna, que tiene un radio de aproximadamente 1080 millas. La aceleración debida a la gravedad en la superficie de la luna es de aproximadamente 5,31 pie/s2. Encuentre la velocidad de escape en millas/s.
19. (a) Demuestre que la Ecuación (9.4.3.23) se puede reescribir como
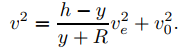
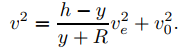
(b) Demuestre que si v0 = ρve con 0 ≤ ρ < 1, entonces la altitud máxima ym alcanzada por el vehículo espacial es


(c) Al exigir que v(ym) = 0, utilice la Ecuación (9.4.3.22) para deducir que si v0 < ve entonces


donde ym y ρ son como se definen en (b) y y ≥ h.
20. En la situación considerada en la discusión de la Velocidad de escape, demuestre que limt→∞ y(t) = ∞ si v(t) > 0 para todo t > 0.
AYUDA: Use una demostración por contradicción. Suponga que existe un número ym tal que y(t) ≤ ym para todo t > 0. Deduzca de esto que existe un número positivo α tal que y′′(t) ≤ −α para todo t ≥ 0. Demuestre que esto contradice la suposición de que v(t) > 0 para todo t > 0.
