| 9. Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden | 9.2.3 Existencia y unicidad de soluciones de ecuaciones no lineales |
Ejercicios propuestos del Capítulo 9.2.3
En los Ejercicios 1 a 13, encuentre todos (x₀, y₀) para los cuales el Teorema 9.2.3.1 implica que el problema de valor inicial y′ = f (x, y), y(x₀) = y₀ tiene (a) una solución (b) una única solución en algún intervalo abierto que contiene x₀.
14. Aplicar el Teorema 9.2.3.1 al problema de valor inicial.
y′ + p(x)y = q(x), y(x₀) = y₀
para una ecuación lineal, y compare las conclusiones que se pueden extraer de ella con las que se derivan del Teorema 9.2.1.2
15. (a) Verifique que la función
es una solución del problema de valor inicial
en (−∞, ∞).
SUGERENCIA: Necesitará la definición
para verificar que y satisface la ecuación diferencial en
(b) Verifique que si εi = 0 o 1 para i = 1, 2 y a, b > 1, entonces la función
es una solución del problema de valor inicial de (a) en (−∞, ∞).
16. Use las ideas desarrolladas en el ejercicio 15 para encontrar infinitas soluciones del problema de valor inicial.
en (−∞, ∞).
17. Considere el problema de valor inicial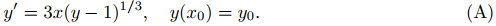
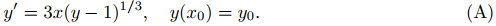
(a) ¿Para qué puntos (x₀, y₀) implica el teorema 9.2.3.1 que (A) tiene una solución?
(b) ¿Para qué puntos(x₀, y₀) implica el teorema 9.2.3.1 que (A) tiene una solución única en algunos intervalo abierto que contiene x₀?
18. Encuentre nueve soluciones del problema de valor inicial.
que estén todas definidas en (−∞, ∞) y difieran entre sí para los valores de x en cada intervalo abierto que contiene x₀ = 0.
19. Del teorema 9.2.3.1, el problema de valor inicial
tiene una solución única en un intervalo abierto que contiene x₀ = 0. Encuentre la solución y determine el intervalo abierto más grande en el que es única.
20. (a) Del teorema 9.2.3.1, el problema de valor inicial
tiene una solución única en algún intervalo abierto que contiene x₀ = 3. Determine el intervalo abierto más grande y encuentre la solución en este intervalo.
(b) Encuentre infinitas soluciones de (A), todas definidas en (−∞, ∞).
21. Demuestre:
(a) Si
y x₀ está en (a, b), entonces y ≡ y₀ es una solución de
en (a, b).
(b) Si f y fy son continuas en un rectángulo abierto que contiene (x₀, y₀) y (A) se cumple, ninguna solución de y′ = f (x, y) distinta de y ≡ y₀ puede ser igual a y₀ en cualquier punto de (a, b).