| 9. Ecuaciones diferenciales | 9.12. Soluciones de Fourier de ecuaciones diferenciales parciales |

9.12.3 La ecuación de Laplace en coordenadas rectangulares |

Ejercicios propuestos para el Capítulo 9.12.2.3

      En los ejercicios 1 a 16, aplique la definición formal desarrollada en el Ejemplo 1 para resolver el problema de valor en la frontera. (Use el Teorema 9.11.3.5 donde corresponda.) Donde este indicado con C, grafique la superficie u = u(x, y),  0 ≤ x ≤ a, 0 ≤ y ≤ b.

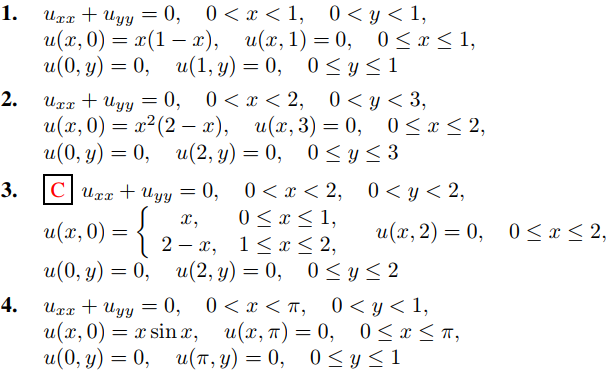
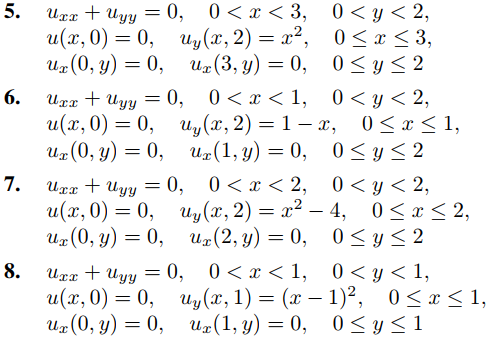
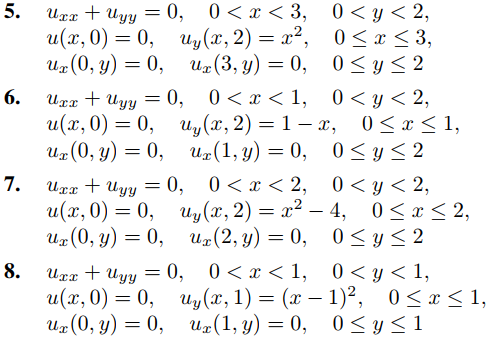
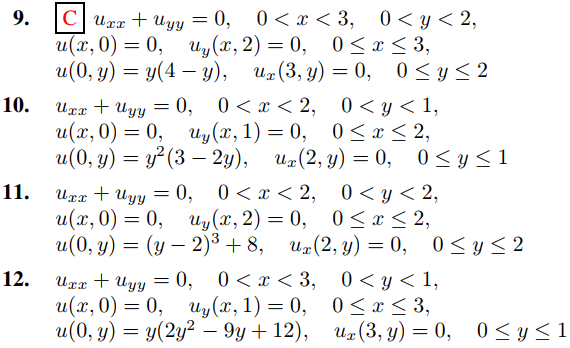
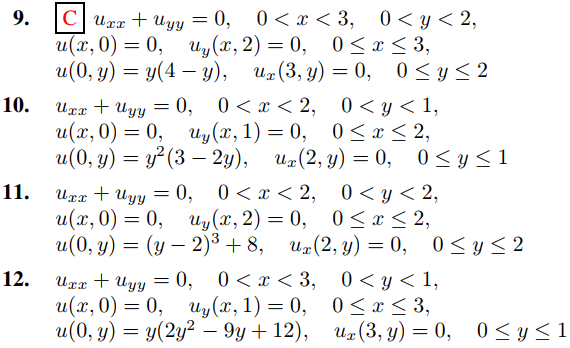
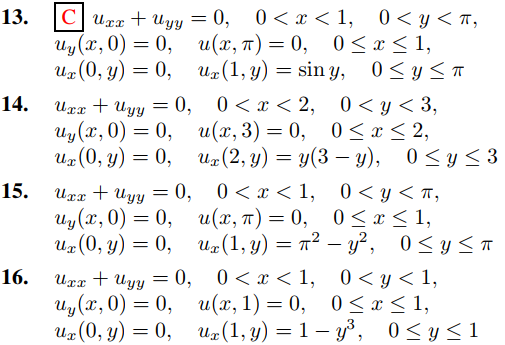
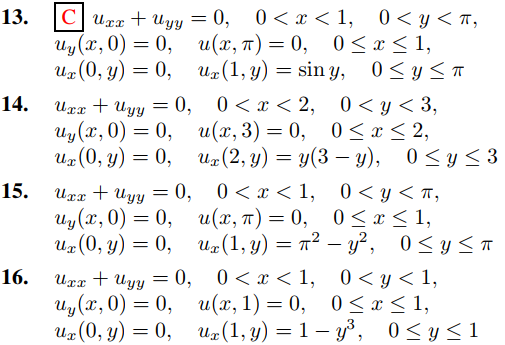
      En los ejercicios 17 a 28 defina la solución formal de

u_xx + u_yy = 0,   0 < x < a,   0 < y < b

que satisfaga las condiciones de contorno dadas para las generales a, b y f o g. Luego resuelva el problema de valores en la frontera para los valores a, b y f o g especificados. (Use el Teorema 9.11.3.5 donde corresponda.) Donde se indique con una C, grafique la superficie u = u(x, y),  0 ≤ x ≤ a, 0 ≤ y ≤ b.

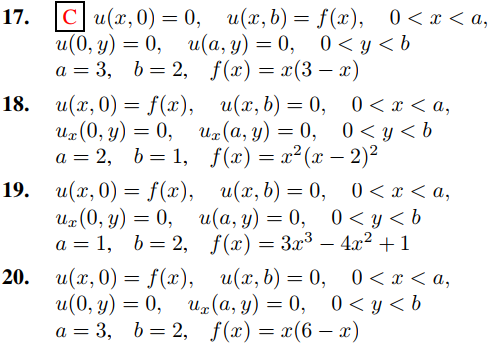
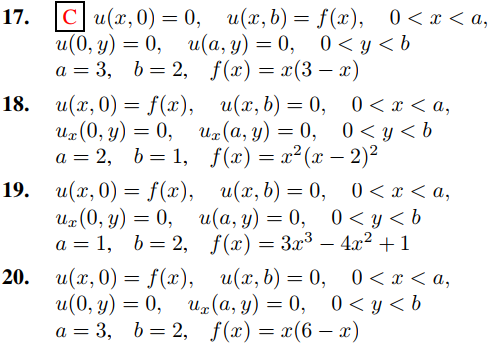
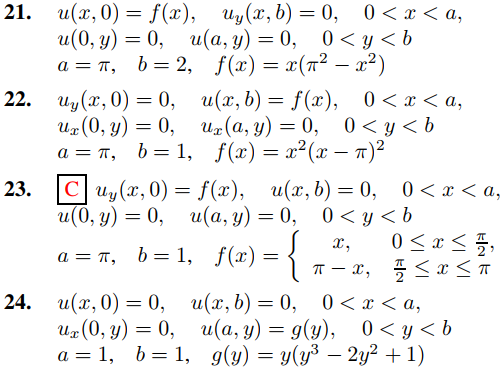
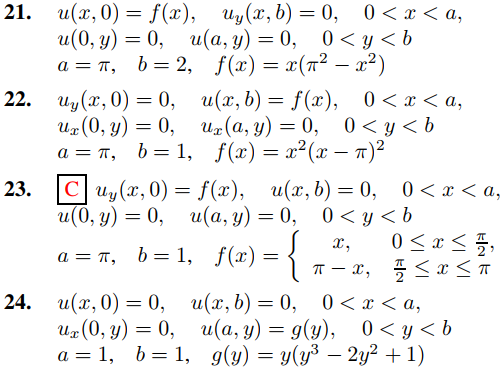
       En los ejercicios 29 a 34 defina la solución formal de

u_xx + u_yy = 0,   0 < x < a,  y > 0

que satisface las condiciones de contorno dadas para las generales a y f. Luego resuelva el problema de valores en la frontera para las a y f especificadas

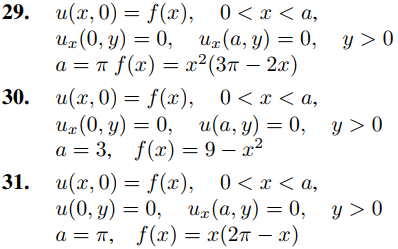
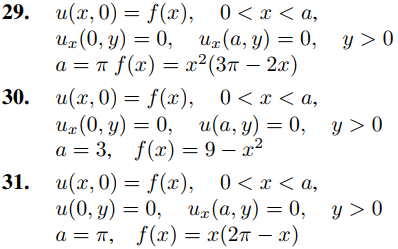
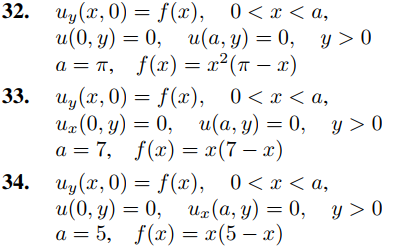
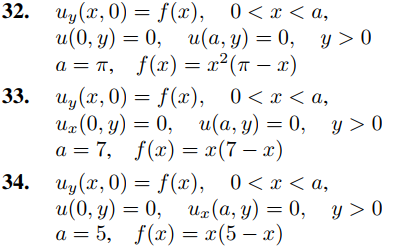
35. Definir la solución formal del problema de Dirichlet

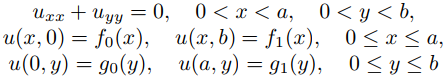
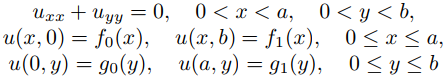
36. Demuestre que el Problema de Neumann

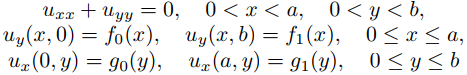
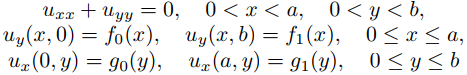
no tiene solución a menos que

En este caso tiene infinitas soluciones formales. Encuéntralas.

37. En este ejercicio se da por sentado que la serie infinita converge para todo p si q > 0, y, en su caso, utilizar la prueba de comparación para la convergencia absoluta de una serie infinita.

Sea

donde

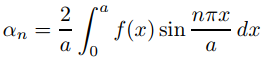
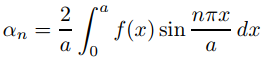
y f es suave por tramos en [0, a].

(a) Verifique las aproximaciones

       (A)

y

       (B)

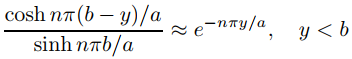
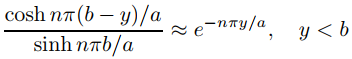
para n grande.

(b) Use (A) para mostrar que u está definido para (x, y) tal que 0 < y < b.

(c) Para y fijo en (0, b), use (A) y el Teorema 9.12.1.1 con z = x para mostrar que

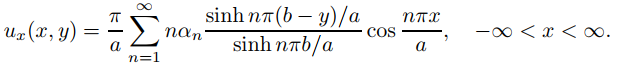
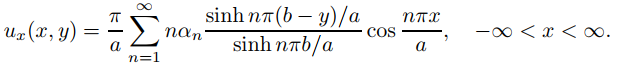
(d) Partiendo del resultado de (b), use (A) y el Teorema 9.12.1.1 con z = x para mostrar que, para una y fija en (0, b),

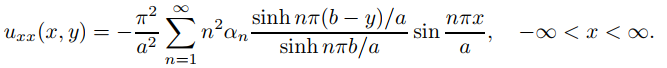
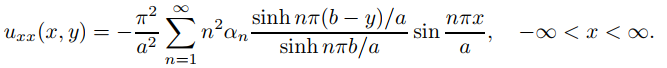
(e) Para x fijo pero arbitrario, use (B) y el Teorema 9.12.1.1 con z = y para mostrar que

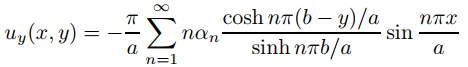
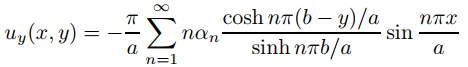
si 0 < y₀ < y < b, donde y₀ es un número arbitrario en (0, b). Luego argumente que dado que y₀ puede elegirse arbitrariamente pequeño, la conclusión se cumple para todo y en (0, b).

(f) Partiendo del resultado de (e), utilice (A) y el Teorema 9.12.1.1 para demostrar que

(g) Concluya que u satisface la ecuación de Laplace para todo (x, y) tal que 0 < y < b.

Al aplicar repetidamente los argumentos de (c) a (f), se puede demostrar que u puede diferenciarse término por término cualquier número de veces con respecto a x y/o y si 0 < y < b.