| 9. Ecuaciones diferenciales | 9.11. Problemas de valores en la frontera y expansiones de Fourier | 9.11.3 Expansiones de Fourier II |
Ejercicios propuestos para el Capítulo 9.11.3
En ejercicios marcados con C grafique f y algunas sumas parciales de la serie requerida. Si el intervalo es [0, L], elija un valor específico de L para el gráfico.
En los Ejercicios 1-10 encuentre la serie del coseno de Fourier.
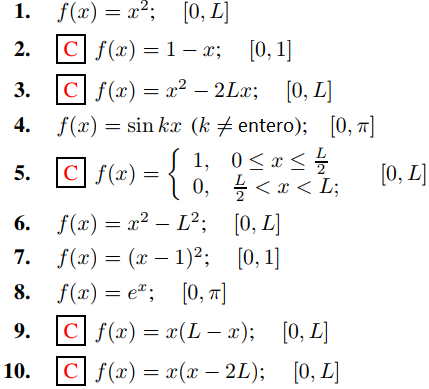
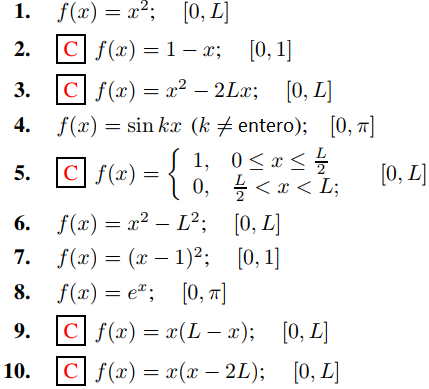
En los ejercicios 11 a 17 encuentre la serie de senos de Fourier.
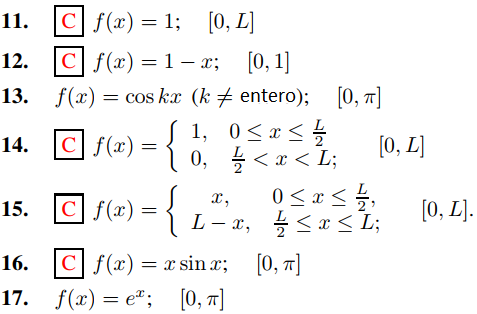
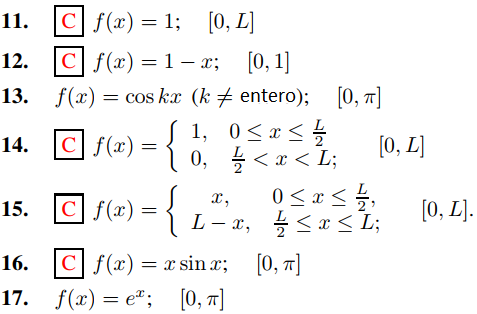
En los ejercicios 18 a 24 encuentre la serie mixta de cosenos de Fourier.
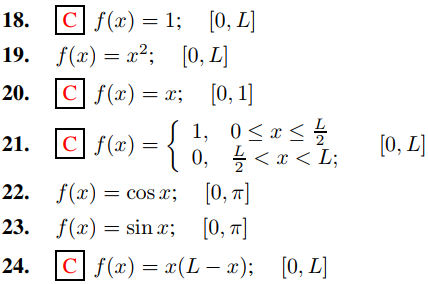
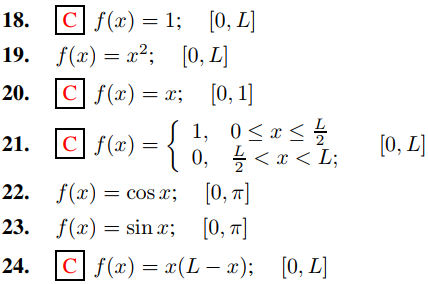
En los ejercicios 25 a 30 encuentre la serie mixta de senos de Fourier.


En los Ejercicios 31–34 use el Teorema 9.11.3.5(a) para encontrar la serie de coseno de Fourier de f en [0, L].


35. (a) Demuestre el Teorema 9.11.3.5(b).
(b) Además de los supuestos del Teorema 9.11.3.5(b), suponga que f ′′(0) = f ′′(L) = 0, f ′′′ es continua y f (4) es continua por partes en [0, L]. Muestre que
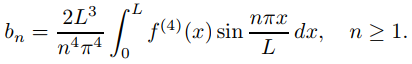
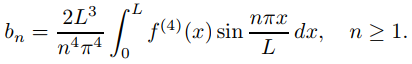
En los Ejercicios 36–41 use el Teorema 9.11.3.5(b) o, donde corresponda, el Ejercicio 9.11.1.35(b), para encontrar la serie de senos de Fourier de f en [0, L].


42. (a) Demuestre el Teorema 9.11.3.5(c).
(b) Además de las suposiciones del Teorema 9.11.3.5(c), suponga que f ′′(L) = 0, f ′′ es continua y f ′′′ es continua por tramos en [0, L]. Muestre que


En los ejercicios 43 a 49, utilice el teorema Teorema 9.11.3.5(c) o, cuando corresponda, el Ejercicio 9.11.1.42(b), para hallar la serie mixta de cosenos de Fourier de f en [0, L].


50. (a) Demuestre el Teorema 9.11.3.5(d).
(b) Además de las suposiciones del Teorema 9.11.3.5(d), suponga que f ′′(0) = 0, f ′′ es continua y f ′′′ es continua por tramos en [0, L]. Muestre que
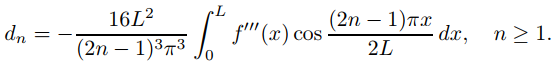
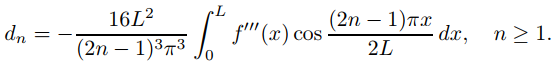
En los Ejercicios 51–56 use el Teorema Teorema 9.11.3.5(d) o, donde corresponda, el Ejercicio 50(b), para encontrar la serie mixta de senos de Fourier de la f en [0, L].
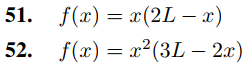
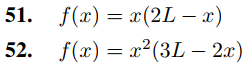
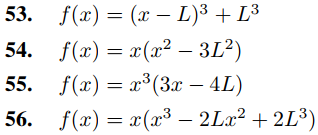
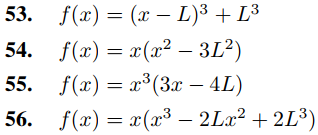
57. Muestre que la serie de coseno de Fourier mixta de f en [0, L] es la restricción a [0, L] de la serie de coseno de Fourier de
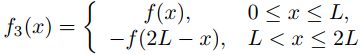
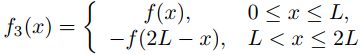
en [0, 2L]. Use esto para probar el Teorema 9.11.3.3.
58. Muestre que la serie de seno de Fourier mixta de f en [0, L] es la restricción a [0, L] de la serie de seno de Fourier de
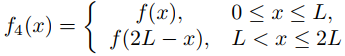
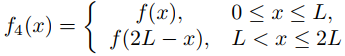
en [0, 2L]. Use esto para demostrar el Teorema 9.11.3.4.
59. Muestre que la serie de seno de Fourier de f en [0, L] es la restricción a [0, L] de la serie de seno de Fourier de
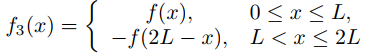
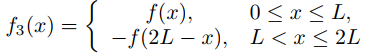
en [0, 2L].
60. Demuestre que la serie de coseno de Fourier de f en [0, L] es la restricción a [0, L] de la serie de coseno de Fourier de
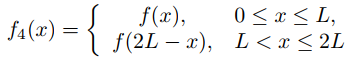
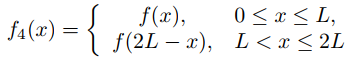
en [0, 2L].
