9. Ecuaciones diferenciales

Ejercicios resueltos del capítulo 9

Ejercicios propuestos para el capítulo 9.10.1

1.  Dos tanques T₁ y T₂ contienen 50 galones y 100 galones de soluciones salinas, respectivamente. Una solución con 2 libras de sal por galón se bombea a T₁ desde una fuente externa a 1 gal/min, y una solución con 3 libras de sal por galón se bombea a T₂ desde una fuente externa a 2 gal/min. La solución de T₁ se bombea a T₂ a 3 gal/min y la solución de T₂ se bombea a T₁ a 4 gal/min. T₁ se drena a 2 gal/min y T₂ se drena a 1 gal/min. Sean Q₁(t) y Q₂(t) el número de libras de sal en T₁ y T₂, respectivamente, en el tiempo t > 0. Deduzca un sistema de ecuaciones diferenciales para Q₁ y Q₂. Suponga que ambas mezclas están bien agitadas.

2.  Dos tanques de 500 galones T₁ y T₂ contienen inicialmente 100 galones cada uno de solución salina. Una solución con 2 libras de sal por galón se bombea a T₁ desde una fuente externa a 6 gal/min, y una solución con 1 libra de sal por galón se bombea a T₂ desde una fuente externa a 5 gal/min. La solución de T₁ se bombea a T₂ a 2 gal/min y la solución de T₂ se bombea a T₁ a 1 gal/min. Ambos tanques se drenan a 3 gal/min. Sea Q₁(t) y Q₂(t) el número de libras de sal en T₁ y T₂, respectivamente, en el tiempo t > 0. Deduzca un sistema de ecuaciones diferenciales para Q₁ y Q₂ que sea válido hasta que un tanque esté a punto de desbordarse. Suponga que ambas mezclas están bien agitadas.

3.  Una masa m₁ está suspendida de un soporte rígido en un resorte S₁ con constante de resorte k₁ y constante de amortiguamiento c₁. Una segunda masa m₂ está suspendida de la primera en un resorte S₂ con constante de resorte k₂ y constante de amortiguamiento c₂, y una tercera masa m₃ está suspendida de la segunda en un resorte S₃ con constante de resorte k₃ y constante de amortiguamiento c₃. Sean y₁ =  y₁(t), y₂ = y₂(t) y y₃ = y₃(t) los desplazamientos de las tres masas desde sus posiciones de equilibrio en el tiempo t, medidos positivos hacia arriba. Deduzca un sistema de ecuaciones diferenciales para y₁, y₂ e y₃, suponiendo que las masas de los resortes son despreciables y que las fuerzas verticales externas F₁, F₂ y F₃ también actúan sobre las masas.

4.  Sea X = x i + y j + z k el vector de posición de un objeto con masa m, expresado en términos de un sistema de coordenadas rectangulares con origen en el centro de la Tierra (Figura 9.10.1.3). Derive un sistema de ecuaciones diferenciales para x, y y z, suponiendo que el objeto se mueve bajo la fuerza gravitacional de la Tierra (dada por la ley de gravitación de Newton, como en el Ejemplo 9.10.1.3) y una fuerza resistiva proporcional a la velocidad del objeto. Sea α la constante de proporcionalidad.

5.  Reescriba el sistema dado como un sistema de primer orden.

6.  Vuelva a escribir el sistema (9.10.1.14) de ecuaciones diferenciales deducido en el Ejemplo 9.10.1.3 como un sistema de primer orden.

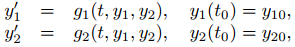
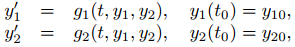
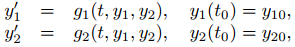
7.  Formule una versión del método de Euler (Sección 9.3.1) para la solución numérica del problema de valor inicialen un intervalo [t₀, b].

8.  Formular una versión del método de Euler mejorado (Sección 9.3.2) para la solución numérica del problema de valor inicialen un intervalo cerrado [t₀, b].