| 9. Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden | 9.2.4. Transformación de ecuaciones no lineales en ecuaciones separables |
Ejercicios propuestos para el Capítulo 9.2.4
En los ejercicios 1 a 4, resuelva la Ecuación de Bernoulli dada.

En los Ejercicios 5 y 6 encuentre todas las soluciones. Además, trace un campo direccional y algunas curvas integrales en la región rectangular indicada.

En los ejercicios 7 a 11 resuelva el problema de valor inicial dado
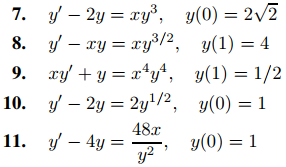
En los Ejercicios 12 y 13 resuelve el problema con valor inicial y representa gráficamente la solución.

14. Es posible que haya notado que la ecuación logística
P′ = aP (1 − αP)
del Modelo de Verhulst para el crecimiento de la población se puede escribir en forma de Bernoulli como
P′ − aP = −aαP2
Esto no es particularmente interesante, ya que la ecuación logística es separable y, por lo tanto, se puede resolver mediante el método estudiado en la Sección 9.2.2. Así que consideremos un modelo más complicado, donde a es una constante positiva y α es una función continua positiva de t en [0, ∞). La ecuación para este modelo es
P′ − aP = −aα(t)P2
una Ecuación de Bernoulli no separable.
(a) Suponiendo que P(0) = P0 > 0, encuentre P para t > 0. AYUDA: Exprese su resultado en términos de la integral 
(b) Verifique que su resultado se reduzca a los resultados conocidos para el Modelo Maltusiano donde α = 0, y el Modelo de Verhulst donde α es una constante distinta de cero.
(c) Suponiendo que

existe (finito o infinito), encuentre limt → ∞ P(t).
En los Ejercicios 15–18 resuelva la ecuación explícitamente.

En los Ejercicios 19–21 resuelve la ecuación explícitamente. Además, trace un campo direccional y algunas curvas integrales en la región rectangular indicada.
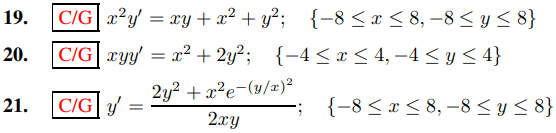
En los Ejercicios 22–27 resuelva el problema de valor inicial

En los Ejercicios 28–34 resuelve implícitamente la ecuación homogénea dada

35. L
(a) Encuentre una solución del problema de valor inicial

en el intervalo (−∞, 0). Verifique que esta solución sea realmente válida en (−∞, ∞).
(b) Use el Teorema 9.2.3.1 para demostrar que (A) tiene una solución única en (−∞, 0).
(c) Trace un campo direccional para la ecuación diferencial en (A) en un cuadrado
{−r ≤ x ≤ r, −r ≤ y ≤ r},
donde r es cualquier número positivo. Grafica la solución que obtuviste en (a) en este campo.
(d) Grafique otras soluciones de (A) que estén definidas en (−∞, ∞).
(e) Grafique otras soluciones de (A) que estén definidas solo en intervalos de la forma (−∞, a), donde es un número positivo finito.
36. L
(a) Resuelva la ecuación

implícitamente.
(b) Trace un campo de dirección para (A) en un cuadrado
{0 ≤ x ≤ r, 0 ≤ y ≤ r}
donde r es cualquier número positivo.
(c) Sea K un entero positivo. (Es posible que deba probar varias opciones para K). Grafique las soluciones de los problemas de valor inicial

para k = 1, 2, . . . , K. Con base en sus observaciones, encuentre condiciones en los números positivos x0 y y0 tales que el problema de valor inicial

tiene solución única (i) en (0, ∞) o (ii) solo en un intervalo (a, ∞), donde a > 0?
(d) ¿Qué puedes decir sobre la gráfica de la solución de (B) cuando x → ∞? (De nuevo, suponga que x0 > 0 y y0 > 0.)
37. L
(a) Resuelva la ecuación

implícitamente.
(b) Trace un campo direccional para (A) en un cuadrado
{−r ≤ x ≤ r, −r ≤ y ≤ r}
donde r es cualquier número positivo. Al graficar las soluciones de (A), determine las condiciones necesarias y suficientes en (x0, y0) tales que (A) tenga una solución en (i) (−∞, 0) o (ii) (0, ∞) tal que y( x0) = y0.
38. L Sigue las instrucciones del Ejercicio 37 para la ecuación

39. L Elija cualquier ecuación homogénea no lineal y′ = q(y/x) que desee, y grafique los campos direccionales en el cuadrado {−r ≤ x ≤ r, −r ≤ y ≤ r}, donde r > 0. ¿Qué sucede con el campo direccional cuando varía r? ¿Por qué?
40. Demostrar: si ad − bc ≠ 0, la ecuación

se puede transformar en la ecuación no lineal homogénea

por la sustitución x = X − X0, y = Y − Y0, donde X0 e Y0 son constantes adecuadamente elegidas.
En los ejercicios 41 a 43 use un método sugerido por el ejercicio 40 para resolver implícitamente la ecuación dada.

En los ejercicios 44 a 51 encuentre una función y1 tal que la sustitución y = uy1 transforme la ecuación dada en una ecuación separable de la forma (9.2.4.6). Luego resuelve la ecuación dada explícitamente.
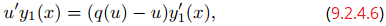

52. Resuelve el problema del valor inicial

53. Resuelve el problema del valor inicial
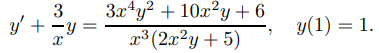
54. Demuestre: si y es una solución de una ecuación no lineal homogénea y′ = q(y/x), también lo es y1 = y(ax)/a, donde a es cualquier constante distinta de cero.
55. Una ecuación de Riccati generalizada tiene la forma

(Si R ≡ −1, (A) es una ecuación de Riccati.) Sea y1 una solución conocida e y una solución arbitraria de (A). Sea z = y − y1. Demuestre que z es una solución de una Ecuación de Bernoulli con n = 2.
En los ejercicios 56 a 59, dado que y1 es una solución de la ecuación dada, use el método sugerido en el Ejercicio 55 para encontrar otras soluciones.
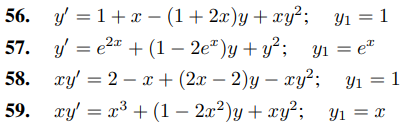
9.2.5: Ecuaciones diferenciales exactas »
