9. Ecuaciones diferenciales y problemas con valores en la frontera
Por:

Índice temático
9.1 Introducción a las ecuaciones diferenciales
- 9.1.1 Algunas aplicaciones que conducen a ecuaciones diferenciales
- 9.1.2 Conceptos básicos
- 9.1.3 Campos direccionales para ecuaciones de primer orden
- Miscelánea de ejercicios resueltos del Capítulo 9.1
9.2 Ecuaciones diferenciales de primer orden
- 9.2.1 Ecuaciones lineales de primer orden
- 9.2.2 Ecuaciones separables
- 9.2.3 Existencia y unicidad de soluciones de ecuaciones no lineales
- 9.2.4 Transformación de ecuaciones no lineales en ecuaciones separables
- 9.2.5 Ecuaciones exactas
- 9.2.6 Factores de integración
- Miscelánea de ejercicios resueltos de Capítulo 9.2
9.3 Métodos numéricos
- 9.3.1 Método de Euler
- 9.3.2 El método de Euler mejorado y métodos relacionados
- 9.3.3 El método Runge-Kutta
9.4 Aplicaciones de ecuaciones de primer orden
- 9.4.1 Crecimiento y decrecimiento
- 9.4.2 Enfriamiento y Mezclas
- 9.4.3 Mecánica elemental
- 9.4.4 Ecuaciones autónomas de segundo orden
- 9.4.5 Aplicaciones a curvas
9.5 Ecuaciones lineales de segundo orden
- 9.5.1 Ecuaciones lineales homogéneas
- 9.5.2 Ecuaciones lineales homogéneas con coeficientes constantes
- 9.5.3 Ecuaciones lineales no homogéneas
- 9.5.4 El método de coeficientes indeterminados I
- 9.5.5 El método de coeficientes indeterminados II
- 9.5.6 Reducción de orden
- 9.5.7 Variación de parámetros
9.6 Aplicaciones de ecuaciones lineales de segundo orden
- 9.6.1 Problemas de resortes I
- 9.6.2 Problemas de resortes II
- 9.6.3 Los circuitos RLC
- 9.6.4 Movimiento bajo una fuerza central
9.7 Soluciones en serie de ecuaciones lineales de segundo orden
- 9.7.1 Revisión de series de potencias
- 9.7.2 Soluciones en serie cerca de un punto ordinario I
- 9.7.3 Soluciones en serie cerca de un punto ordinario II
- 9.7.4 Ecuaciones de Euler de puntos singulares regulares
- 9.7.5 El método de Frobenius I
- 9.7.6 El método de Frobenius II
- 9.7.7 El método de Frobenius III
9.8 La transformada de Laplace
- 9.8.1 Introducción a la transformada de Laplace
- 9.8.2 La transformada inversa de Laplace
- 9.8.3 Solución de problemas de valor inicial
- 9.8.4 La función escalón unitario
- 9.8.5 Ecuaciones de coeficientes constantes con funciones de forzamiento continuas por tramos
- 9.8.6 Convolución
- 9.8.7 Ecuaciones de coeficientes constantes con impulsos
- 9.8.8 Tabla de transformadas de Laplace
9.9 Ecuaciones lineales de orden superior
- 9.9.1 Introducción a las ecuaciones lineales de orden superior
- 9.9.2 Ecuaciones homogéneas de coeficientes constantes de orden superior
- 9.9.3 Coeficientes indeterminados para ecuaciones de orden superior
- 9.9.4 Variación de parámetros para ecuaciones de orden superior
9.10 Sistemas de ecuaciones diferenciales lineales
- 9.10.1 Introducción a los sistemas de ecuaciones diferenciales
- 9.10.2 Sistemas de ecuaciones diferenciales lineales
- 9.10.3 Teoría básica de sistemas lineales homogéneos
- 9.10.4 Sistemas homogéneos con coeficientes constantes I
- 9.10.5 Sistemas homogéneos con coeficientes constantes II
- 9.10.6 Sistemas homogéneos con coeficientes constantes III
- 9.10.7 Variación de parámetros para sistemas lineales no homogéneos
9.11 Problemas con valores en la frontera y expansiones de Fourier
- 9.11.1 Problemas de valor propio (eigenvalores)
- 9.11.2 Expansiones de Fourier I
- 9.11.3 Expansiones de Fourier II
9.12 Soluciones de Fourier de ecuaciones diferenciales parciales
- 9.12.1 La ecuación de calor
- 9.12.2 La ecuación de onda
- 9.12.3 La ecuación de Laplace en coordenadas rectangulares
- 9.12.4 La ecuación de Laplace en coordenadas polares
9.13 Problemas de valores en la frontera para ecuaciones diferenciales ordinarias de segundo orden
¡Apoya nuestro trabajo!
Requisitos previos y público objetivo
Ecuaciones diferenciales elementales con problemas de valores en la frontera está escrito para estudiantes de ciencias, ingeniería y matemáticas que han cursado cálculo hasta la diferenciación parcial. Si el programa incluye el Capítulo 9.10 Sistemas de ecuaciones diferenciales lineales, los estudiantes deberían tener alguna preparación en álgebra lineal.
Principios que guiaron la elaboración de este libro
-
Un texto elemental debe redactarse de manera que el estudiante pueda leerlo y comprenderlo sin excesiva dificultad. Se privilegia la claridad y el detalle, optando por ofrecer explicaciones abundantes antes que insuficientes.
-
La calidad de un texto elemental depende en gran medida de sus ejercicios. Por esta razón, el presente libro incluye 2041 ejercicios numerados, muchos de ellos con varias partes. El nivel de dificultad se extiende desde lo rutinario hasta lo altamente desafiante.
-
Un texto elemental debe escribirse en un estilo accesible e informal, pero matemáticamente preciso. Los conceptos matemáticos se presentan de manera concisa, en un lenguaje comprensible para los estudiantes. Se reduce al mínimo el número de teoremas y definiciones enunciados explícitamente, prefiriéndose un tratamiento más conversacional, ilustrado con 299 ejemplos completamente desarrollados. En situaciones pertinentes, los conceptos y resultados se representan gráficamente mediante figuras ilustrativas, en total 188.
Flexibilidad pedagógica y uso de tecnología
Aunque la computadora constituye una herramienta de gran valor para aprender, desarrollar y redactar matemáticas, la selección y el tratamiento de los temas en este texto responden a una orientación pedagógica de carácter tradicional. No obstante, se ha incorporado el mejor uso posible de la tecnología moderna, de modo que cada docente pueda seleccionar el nivel de tecnología que desee incluir en su curso. El texto contiene 414 ejercicios — identificados con los símbolos C y C/G — que requieren gráficos o cálculos acompañados de gráficos. Asimismo, se incluyen 79 ejercicios de laboratorio — identificados con L — que demandan un uso intensivo de la tecnología. Además, varias secciones ofrecen recomendaciones informales sobre el empleo de herramientas tecnológicas. Quienes prefieran no enfatizar la tecnología pueden simplemente omitir estos ejercicios y las recomendaciones asociadas.
Organización de técnicas y aplicaciones
Existen dos enfoques respecto a si las técnicas y las aplicaciones deben tratarse de manera conjunta o separada. En este texto se ha optado por la separación: el Capítulo 9.2 Ecuaciones diferenciales de primer orden aborda las técnicas para resolver ecuaciones de primer orden, mientras que el Capítulo 9.4 Aplicaciones de ecuaciones de primer orden se dedica a las aplicaciones. De manera similar, el Capítulo 9.5 Ecuaciones lineales de segundo orden trata las técnicas para resolver ecuaciones de segundo orden y el Capítulo 9.6 Aplicaciones de ecuaciones lineales de segundo orden sus aplicaciones. Sin embargo, los conjuntos de ejercicios de las secciones dedicadas a técnicas incluyen también algunos problemas aplicados.
Más allá de los métodos inconexos: Un enfoque integrado
Los textos elementales de ecuaciones diferenciales con orientación tradicional suelen ser criticados por presentarse como colecciones de métodos inconexos para resolver problemas diversos. En cierta medida esto es cierto, ya que ningún método único resulta aplicable a todas las situaciones. Sin embargo, una idea puede contribuir significativamente a unificar varias de las técnicas empleadas en la resolución de problemas distintos: la variación de parámetros. Este recurso se introduce desde la Sección 9.2.1 Ecuaciones lineales de primer orden para resolver la ecuación lineal no homogénea, partiendo de una solución no trivial de la ecuación complementaria. Aunque tradicionalmente se enseña que para esta tarea deben emplearse factores integrantes, y que la variación de parámetros se menciona solo como alternativa en algunos ejercicios, en realidad ambas aproximaciones difieren poco, pues un factor integrante no es más que el recíproco de una solución no trivial de la ecuación complementaria. La ventaja de introducir la variación de parámetros en este punto es que se presenta en su forma más simple y dirige la atención del estudiante hacia la idea de buscar una solución y de una ecuación diferencial escribiéndola como y = uy1, donde y1 es una solución conocida de una ecuación relacionada y u es una función por determinar.
Este enfoque se aplica de manera no convencional en distintos contextos:
-
En la Sección 9.2.4, para resolver ecuaciones no lineales de primer orden, como las ecuaciones de Bernoulli y las ecuaciones homogéneas no lineales.
-
En el Capítulo 9.3, para la solución numérica de ecuaciones semilineales de primer orden.
-
En la Sección 9.5.2, para evitar la necesidad de introducir exponenciales complejos al resolver una ecuación homogénea de segundo orden con coeficientes constantes y polinomios característicos con raíces complejas.
-
En las Secciones 9.5.4, 9.5.5 y 9.9.3, en el contexto del método de coeficientes indeterminados. (Si se prefiere el método de aniquiladores, resulta ilustrativo comparar el esfuerzo requerido para resolver, por ejemplo, y′′ + y′ + y = x4ex mediante dicho método y el procedimiento expuesto en la Sección 9.5.4).
- Introducir la variación de parámetros lo antes posible (Sección 9.2.1) prepara al estudiante para el concepto cuando vuelva a aparecer en formas más complejas en la Sección 9.5.6, donde la reducción de orden se utiliza no solo para encontrar una segunda solución de la ecuación complementaria, sino también para encontrar la solución general de la ecuación no homogénea, y en las Secciones 9.5.7, 9.9.4 y 9.10.7, que tratan el problema usual de variación de parámetros para ecuaciones lineales de segundo y mayor orden y para sistemas lineales.
Series de Fourier y problemas de valores propios
El Capítulo 9.11 desarrolla la teoría de las series de Fourier. La Sección 9.11.1 analiza los cinco principales problemas de valores propios que surgen en relación con el método de separación de variables para las ecuaciones de calor y de onda y para la ecuación de Laplace en un dominio rectangular: 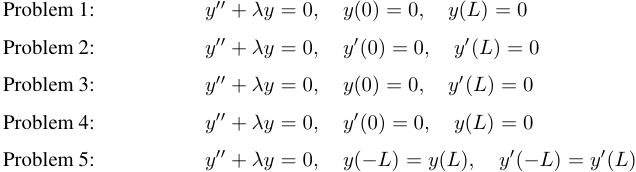
Estos problemas se abordan de manera unificada; por ejemplo, un único teorema muestra que los valores propios de los cinco problemas son no negativos. La Sección 9.11.2 presenta la expansión en series de Fourier de funciones definidas en [−L, L], interpretándola como una expansión en términos de las funciones propias del Problema 5. La Sección 9.11.3 presenta las expansiones de Fourier en senos y cosenos de funciones definidas en [0, L], interpretándolas como expansiones en términos de las funciones propias de los Problemas 1 y 2, respectivamente. Además, la Sección 9.11.2 incluye lo que llamo las expansiones mixtas de Fourier en senos y cosenos, en términos de las funciones propias de los Problemas 4 y 5, respectivamente. En todos los casos, las propiedades de convergencia de estas series se deducen de las propiedades de convergencia de la serie de Fourier discutidas en la Sección 9.11.1.
Separación de variables y validez de las soluciones reales en ecuaciones del calor, de ondas y de Laplace
El Capítulo 9.12 consta de cuatro secciones dedicadas a la ecuación del calor, la ecuación de onda y la ecuación de Laplace en coordenadas rectangulares y polares. Para las tres, considero condiciones de contorno homogéneas de los cuatro tipos que aparecen en los Problemas 1 – 4. Presento el método de separación de variables como una forma de elegir la forma apropiada para la expansión en series de la solución del problema dado, indicando —sin insistir demasiado— que la expansión puede no ser una solución real, y dando una indicación de las condiciones bajo las cuales la solución formal es una solución real. En particular, encontré necesario dedicar cierto detalle a esta cuestión en relación con la ecuación de onda en la Sección 9.12.2.
En las Secciones 9.12.1 (La ecuación del calor) y 9.12.2 (La ecuación de ondas) dedico un esfuerzo considerable a elaborar ejemplos y numerosos ejercicios en los que las funciones que definen las condiciones iniciales satisfacen las condiciones de frontera homogéneas. De manera similar, en la mayoría de los ejemplos y ejercicios de la Sección 9.12.3 (La ecuación de Laplace), las funciones que definen las condiciones de frontera en un lado dado del dominio rectangular cumplen condiciones de frontera homogéneas en los extremos, del mismo tipo (Dirichlet o Neumann) que las condiciones de frontera impuestas en los lados adyacentes de la región. Por lo tanto, las soluciones formales obtenidas en muchos de los ejemplos y ejercicios son soluciones reales.
Problemas de valor en dos puntos, funciones de Green y teoría de Sturm–Liouville
La Sección 9.13.1 trata sobre problemas de valor en dos puntos para una ecuación diferencial ordinaria de segundo orden. Se dan las condiciones para la existencia y unicidad de las soluciones, e incluye la construcción de funciones de Green.
La Sección 9.13.2 presenta los aspectos elementales de la teoría de Sturm-Liouville.
Observaciones adicionales y sugerencias para la selección del programa de estudios
También puede resultarle de interés lo siguiente:
-
La Sección 9.2.6 trata de factores integrantes de la forma µ = p(x)q(y), además de aquellos de la forma µ = p(x) y µ = q(y) discutidos en la mayoría de los textos.
-
La Sección 9.4.4 hace accesible el análisis del plano de fases de ecuaciones autónomas no lineales de segundo orden a estudiantes que no han cursado álgebra lineal, ya que valores y vectores propios no intervienen en el tratamiento. El análisis del plano de fases de sistemas lineales con coeficientes constantes se incluye en las Secciones 9.10.4–6.
-
La Sección 9.4.5 presenta una amplia discusión de aplicaciones de las ecuaciones diferenciales a curvas.
-
La Sección 9.6.4 estudia el movimiento bajo una fuerza central, lo cual puede ser útil para estudiantes interesados en la matemática de las órbitas satelitales.
-
Las Secciones 9.7.5–7 presentan el método de Frobenius con más detalle que la mayoría de los textos. El enfoque consiste en sistematizar los cálculos de manera que se evite la necesidad de sustituir la serie de Frobenius desconocida en cada ecuación. Esto conduce a eficiencia en el cálculo de los coeficientes de la solución de Frobenius. También aclara el caso en que las raíces de la ecuación indicial difieren en un número entero (Sección 9.7.7).
-
El Manual gratuito de soluciones para estudiantes contiene soluciones de la mayoría de los ejercicios con numeración par.
-
El Manual gratuito de soluciones para instructores está disponible por correo electrónico a wtrench@trinity.edu, sujeto a verificación del estatus docente del solicitante.
Las siguientes observaciones pueden ser útiles al elegir su programa de estudios:
-
La Sección 9.2.3 es el único prerrequisito específico para el Capítulo 9.3. Para acomodar instituciones que ofrecen un curso separado de análisis numérico, el Capítulo 9.3 no es prerrequisito para ninguna otra sección del texto.
-
Las secciones del Capítulo 9.4 son independientes entre sí y no son prerrequisitos para ninguno de los capítulos posteriores. Esto también es cierto para las secciones del Capítulo 9.6, excepto que la Sección 9.6.1 es prerrequisito para la Sección 9.6.2.
-
Los Capítulos 9.7, 9.8 y 9.9 pueden cubrirse en cualquier orden después de los temas seleccionados del Capítulo 9.5. Por ejemplo, puede pasar directamente del Capítulo 9.5 al Capítulo 9.9.
-
La ecuación de Euler de segundo orden se discute en la Sección 9.7.4, donde prepara el terreno para el método de Frobenius. Como se señala al inicio de la Sección 9.7.4, si desea incluir ecuaciones de Euler en su programa de estudios omitiendo el método de Frobenius, puede saltarse los párrafos introductorios de la Sección 9.7.4 y comenzar con la Definición 9.7.4.2. Luego puede cubrir la Sección 9.7.4 inmediatamente después de la Sección 9.5.2.
-
Los Capítulos 9.11, 9.12 y 9.13 pueden cubrirse en cualquier momento después de completar el Capítulo 9.5.
¡Apoya nuestro trabajo!
Ejercicios resueltos del Capítulo 9:
- Dennis G. Zill (Ed. 7 y 9)
- Dennis G. Zill (Ed. 7)
- Edwards y Penney (Ed. 4)
- Manual gratuito de soluciones para estudiantes
Muchos fenómenos del mundo natural pueden modelarse matemáticamente utilizando ecuaciones diferenciales. El crecimiento de una población, la desintegración radiactiva, los modelos depredador-presa y los sistemas de masa resorte son cuatro ejemplos de tales fenómenos.

Supongamos que deseamos estudiar una población de ciervos a lo largo del tiempo y determinar el número total de animales en un área determinada. Primero podemos observar a la población durante un período de tiempo, estimar el número total de venados y luego usar varios supuestos para derivar un modelo matemático para diferentes escenarios. Algunos factores que a menudo se consideran son el impacto ambiental, los valores límite de la población y los depredadores. En estas lecciones del capítulo veremos, por ejemplo, cómo se pueden usar las ecuaciones diferenciales para predecir poblaciones a lo largo del tiempo.
