| 9. Ecuaciones diferenciales |
9.13 Problemas con valores en la frontera para ecuaciones diferenciales ordinarias de segundo orden
EN ESTE CAPÍTULO analizamos problemas de valores en la frontera y problemas de valores propios para ecuaciones diferenciales ordinarias lineales de segundo orden.
La Sección 9.13.1 analiza los problemas de valores en la frontera de dos puntos para ecuaciones diferenciales ordinarias lineales de segundo orden.
La Sección 9.13.2 trata de las generalizaciones de los problemas de valores propios considerados en la Sección 9.11.1.
9.13.1 PROBLEMAS DE VALORES EN LA FRONTERA DE DOS PUNTOS
En la Sección 9.5.3 consideramos problemas de valor inicial para la ecuación lineal de segundo orden
P0(x)y′′ + P1(x)y′ + P2(x)y = F(x). (9.13.1.1)
Suponga que P0, P1, P2 y F son continuos y P0 no tiene ceros en un intervalo abierto (a, b). Del Teorema 9.5.3.1, si x0 está en (a, b) y k1 y k2 son números reales arbitrarios, entonces (9.13.1.1) tiene una solución única en (a, b) tal que y(x0) = k1 y y′ (x0) = k2. Ahora consideramos un problema diferente para (9.13.1.1).
PROBLEMA
Suponga que P0, P1, P2 y F son continuos y P0 no tiene ceros en un intervalo cerrado [a, b]. Sean α, β, ρ y δ números reales tales que
α2 + β2 ≠ 0 y ρ2 + δ2 ≠ 0, (9.13.1.2)
y sean k1 y k2 números reales arbitrarios. Encuentre una solución de
P0(x)y′′ + P1(x)y′ + P2(x)y = F(x) (9.13.1.3)
en el intervalo cerrado [a, b] tal que
αy(a) + βy′(a) = k1 (9.13.1.4)
y
ρy(b) + δy′(b) = k2. (9.13.1.5) ♦
Las suposiciones establecidas en este problema se aplican a lo largo de esta sección y no se repetirán. Observe que imponemos condiciones a P0, P1, P2 y F en el intervalo cerrado [a, b], y estamos interesados en las soluciones de (9.13.1.3) en este intervalo cerrado. Esto es diferente de la situación considerada en el Capítulo 9.5, donde impusimos condiciones en P0, P1, P2 y F en el intervalo abierto (a, b) y estábamos interesados en soluciones en el intervalo abierto. Realmente no hay problema aquí; siempre podemos extender P0, P1, P2 y F a un intervalo abierto (c, d) (por ejemplo, definiéndolos como constantes en (c, d] y [b, d)) para que sean continuos y P0 no tiene ceros en [c, d]. Entonces podemos aplicar los teoremas del Capítulo 5 a la ecuación
en (c, d) para sacar conclusiones sobre las soluciones de (9.13.1.3) en [a, b].
Llamamos a lo extremos a y b puntos frontera. Las condiciones (9.13.1.4) y (9.13.1.5) son condiciones de contorno y el problema es un problema de valor de contorno de dos puntos o, para simplificar, un problema de valor de contorno. (Usamos una terminología similar en el Capítulo 9.12 con un significado diferente; ambos significados son de uso común). Requerimos (9.13.1.2) para asegurarnos de que estamos imponiendo una condición sensata en cada punto frontera. Por ejemplo, si α2 + β2 = 0 entonces α = β = 0, entonces αy(a) + βy′(a) = 0 para todas las elecciones de y(a) y y′(a). Por lo tanto (9.13.1.4) es una condición imposible si k1 ≠ 0, o ninguna condición si k1 = 0.
Abreviamos (9.13.1.1) como Ly = F, donde
Ly = P0(x)y′′ + P1(x)y′ + P0(x)y,
y denotamos
B1(y) = αy(a) + βy′(a) y B2(y) = ρy(b) + δy′(b).
Combinamos (9.13.1.3), (9.13.1.4) y (9.13.1.5) como
Ly = F, B1(y) = k1, B2(y) = k2. (9.13.1.6)
Este problema de valores en la frontera es homogéneo si F = 0 y k1 = k2 = 0; de lo contrario, es no homogéneo.
Te dejamos (Ejercicio 1) comprobar que B1 y B2 son operadores lineales; es decir, si c1 y c2 son constantes entonces
Bi(c1y1 + c2y2) = c1Bi(y1) + c2Bi(y2), i = 1, 2. (9.13.1.7)
Los tres ejemplos siguientes muestran que la cuestión de la existencia y unicidad de las soluciones de los problemas de valores en la frontera es más complicada que la de los problemas de valores iniciales.
Ejemplo ilustrativo 9.13.1.1
Considere el problema de valores en la frontera
y′′ + y = 1, y(0) = 0, y(π/2) = 0.
La solución general de y′′ + y = 1 es
y = 1 + c1senx + c2cosx,
entonces y(0) = 0 si y solo si c2 = −1 y y(π/2) = 0 si y solo si c1 = −1. Por lo tanto
y = 1 − senx − cosx
es la solución única del problema de valores en la frontera. ♦
Ejemplo ilustrativo 9.13.1.2
Considere el problema de valores en la frontera
y′′ + y = 1, y(0) = 0, y(π) = 0.
La solución general de y′′ + y = 1 es
y = 1 + c1senx + c2cosx,
entonces y(0) = 0 si y solo si c2 = −1, pero y(π) = 0 si y solo si c2 = 1. Por lo tanto, el problema de valor en la frontera no tiene solución. ♦
Ejemplo ilustrativo 9.13.1.3
Considere el problema de valores en la frontera
y′′ + y = sen2x, y(0) = 0, y(π) = 0.
Puedes usar el método de los coeficientes indeterminados (Sección 9.5.5) para encontrar que la solución general de y′′ + y = sen2x es
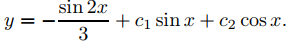
Las condiciones de frontera y(0) = 0 y y(π) = 0 requieren que c2 = 0, pero no restringen c1.
Por lo tanto, el problema de valores en la frontera tiene infinitas soluciones.
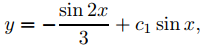
Donde c1 es arbitraria. ♦
Teorema 9.13.1.1
Si z1 y z2 son soluciones de Ly = 0 tales que B1(z1) = B1(z2) = 0 o B2(z1) = B2(z2) = 0, entonces {z1, z2} es linealmente dependiente. De manera equivalente, si {z1, z2} es linealmente independiente
B12(z1) + B12(z2) ≠ 0 y B22(z1) + B22(z2) ≠ 0. ♦
Demostración:
Recuerda que B1(z) = αz(a) + βz′(a) y α2 +β2≠ 0. Por lo tanto, si B1(z1) = B1(z2) = 0 entonces (α, β) es una solución no trivial de el sistema
Esto implica que
z1(a)z2′(a) − z1′(a)z2(a) = 0,
entonces {z1, z2} es linealmente dependiente, por el Teorema 9.5.1.6. Le dejamos a usted demostrar que {z1, z2} es linealmente dependiente si B2(z1) = B2(z2) = 0. ♦
Teorema 9.13.1.2
Las siguientes declaraciones son equivalentes; es decir, son todas verdaderas o todas falsas.
(a) Hay un conjunto fundamental {z1, z2} de soluciones de Ly = 0 tal que
B1(z1)B2(z2) − B1(z2)B2(z1) ≠ 0. (9.13.1.8)
(b) Si {y1, y2} es un conjunto fundamental de soluciones de Ly = 0 entonces
B1(y1)B2(y2) − B1(y2)B2(y1) ≠ 0. (9.13.1.9)
(c) Para cada F continua y par de constantes (k1, k2), el problema de valores en la frontera
Ly = F, B1(y) = k1, B2(y) = k2
tiene una solución única.
(d) El problema de valores en la frontera homogéneo
Ly = 0, B1(y) = 0, B2(y) = 0 (9.13.1.10)
tiene solo la solución trivial y = 0.
(e) La ecuación homogénea Ly = 0 tiene soluciones linealmente independientes z1 y z2 tales que B1(z1) = 0 y B2(z2) = 0. ♦
Demostración:
Mostraremos que (a) ⇒ (b) ⇒ (c) ⇒ (d) ⇒ (e) ⇒ (a).
(a) ⇒ (b): Dado que {z1, z2} es un conjunto fundamental de soluciones para Ly = 0, existen constantes a1, a2, b1 y b2 tales que
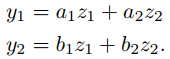(9.13.1.11)
Además,
(9.13.1.12)
porque si este determinante fuera cero, sus filas serían linealmente dependientes y, por lo tanto, {y1, y2} serían linealmente dependientes, contrariamente a nuestra suposición de que {y1, y2} es un conjunto fundamental de soluciones de Ly = 0. De (9.13. 1.7) y (9.13.1.11),
Dado que el determinante de un producto de matrices es el producto de los determinantes de las matrices, (9.13.1.8) y (9.13.1.12) implican (9.13.1.9).
(b) ⇒ (c): Dado que {y1, y2} es un conjunto fundamental de soluciones de Ly = 0, la solución general de Ly = F es
y = yp + c1y1 + c2y2,
donde c1 y c2 son constantes arbitrarias y yp es una solución particular de Ly = F. Para satisfacer las condiciones de contorno, debemos elegir c1 y c2 de modo que
(tener presente (9.13.1.7)), que es equivalente a
De (9.13.1.9), este sistema siempre tiene solución única (c1, c2).
(c) ⇒ (d): Obviamente, y = 0 es una solución de (9.13.1.10). De (c) con F = 0 y k1 = k2 = 0, es la única solución.
(d) ⇒ (e): Sea {y1, y2} un sistema fundamental para Ly = 0 y sea
z1 = B1(y2)y1 − B1(y1)y2 y z2 = B2(y2)y1 − B2(y1)y2.
Entonces B1(z1) = 0 y B2(z2) = 0. Para ver que z1 y z2 son linealmente independientes, observe que
Por lo tanto, dado que y1 e y2 son linealmente independientes, a1z1 + a2z2 = 0 si y solo si
Si este sistema tiene una solución no trivial, también la tiene el sistema
Esto y (9.13.1.7) implican que y = c1z1 + c2z2 es una solución no trivial de (9.13.1.10), que contradice (d).
(e) ⇒ (a). El teorema 9.13.1.1 implica que si B1(z1) = 0 y B2(z2) = 0 entonces B1(z2) ≠ 0 y B2(z1) ≠ 0. Esto implica (13.1.8), que completa la demostración. ♦
Ejemplo ilustrativo 9.13.1.4
Resolver el problema de valores en la frontera
x2y′′ − 2xy′ + 2y − 2x3 = 0, y(1) = 4, y′(2) = 3, (9.13.1.13)
dado que {x, x2} es un conjunto fundamental de soluciones de la ecuación complementaria.
Solución:
Usando la variación de parámetros (Sección 9.5.7), puede demostrar que yp = x3 es una solución de la ecuación complementaria
x2y′′ − 2xy′ + 2y = 2x3 = 0.
Por tanto, la solución de (9.13.1.13) se puede escribir como
y = x3 + c1x + c2x2.
Entonces
y′ = 3x2 + c1 + 2c2x,
e imponiendo las condiciones de contorno se obtiene el sistema
entonces c1 = 7 y c2 = −4. Por lo tanto
y = x3 + 7x − 4x2
es la solución única de (9.13.1.13). ♦
Ejemplo ilustrativo 9.13.1.5
Resolver el problema de valores en la frontera
y′′ − 7y′ + 12y = 4e2x, y(0) = 3, y(1) = 5e2.
Solución:
Del Ejemplo 9.5.4.1, yp = 2e2x es una solución particular de
y′′ − 7y′ + 12y = 4e2x (9.13.1.14)
Como {e3x, e4x} es un conjunto fundamental para la ecuación complementaria, podríamos escribir la solución de (13.1.14) como
y = 2e2x + c1e3x + c2e4x
y determine c1 y c2 imponiendo las condiciones de contorno. Sin embargo, esto conduciría a un álgebra tediosa, y la forma de la solución sería muy poco atractiva. (¡Pruébelo!) En este caso es conveniente utilizar el sistema fundamental {z1, z2} mencionado en el Teorema 9.13.1.2(e); es decir, elegimos {z1, z2} de modo que B1(z1) = z1(0) = 0 y B2(z2) = z2(1) = 0. Es fácil ver que
z1 = e3x − e4x y z2 = e3(x − 1) − e4(x − 1)
satisfacer estos requisitos. Ahora escribimos la solución de (9.13.1.14) como
Al imponer las condiciones de contorno y(0) = 3 y y(1) = 5e2 se obtiene
3 = 2 + c2e − 4(e − 1) y 5e2 = 2e2 + c1e3(1 − e).
Por lo tanto
y
♦
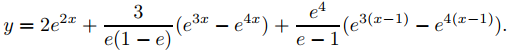A veces es útil tener una fórmula para la solución de un problema en la frontera general. Nuestro siguiente teorema responde a esta pregunta.
Teorema 9.13.1.3
Supongamos que el problema de valores en la frontera homogéneo
Ly = 0, B1(y) = 0, B2(y) = 0 (9.13.1.15)
tiene sólo la solución trivial. Sean y1 e y2 soluciones linealmente independientes de Ly = 0 tales que B1(y1) = 0 y B2(y2) = 0, y sea
W = y1y2′ − y1′ y2.
Entonces la solución única de
Ly = F, B1(y) = 0, B2(y) = 0 (13.1.16)
es
(13.1.17) ♦
Prueba:
En la Sección 9.5.7 vimos que si
y = u1y1 + u2y2 (9.13.1.18)
donde
entonces Ly = F. Resolviendo para u1′ y u2′ se obtiene
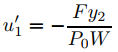y 
que se mantiene si
y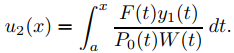 
Esto y (9.13.1.18) muestran que (9.13.1.17) es una solución de Ly = F. Derivando (9.13.1.17) se obtiene
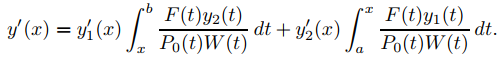(9.13.1.19)
(Verificar.) De (9.13.1.17) y (9.13.1.19),
porque B1(y1) = 0, y
porque B2(y2) = 0. Por lo tanto, y satisface (9.13.1.16). Esto completa la demostración. ♦
Podemos reescribir (9.13.1.17) como
(9.13.1.20)
donde
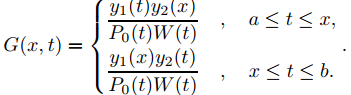
Esta es la función de Green para el problema de valores en la frontera (9.13.1.16). La función de Green está relacionada con el problema de valores en la frontera (9.13.1.16) de la misma manera que la inversa de una matriz cuadrada A está relacionada con el sistema algebraico lineal y = Ax; así como sustituimos el vector y dado en la fórmula x = A−1y para resolver y = Ax, sustituimos la función F dada en la fórmula (9.13.1.20) para obtener la solución de (9.13.1.16). La analogía va más allá: así como A−1 existe si y solo si Ax = 0 tiene solo la solución trivial, el problema de valores en la frontera (9.13.1.16) tiene una función de Green si y solo el problema de valores en la frontera homogéneo (9.13.1.15) tiene sólo la solución trivial.
Le dejamos a usted (Ejercicio 32) demostrar que los supuestos del Teorema 9.13.1.3 implican que la solución única del problema de valores en la frontera
Ly = F, B1(y) = k1, B2(y) = k2
es
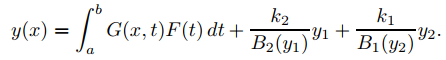
Ejemplo ilustrativo 9.13.1.6
Resolver el problema del valores en la frontera
y′′ + y = F(x). y(0) + y′(0) = 0, y(π) − y′(π) = 0, (9.13.1.21)
y encuentre la función de Green para este problema.
Solución:
Aquí
B1(y) = y(0) + y′(0) y B2(y) = y(π) − y′(π).
Sea {z1, z2} = {cosx, senx}, que es un conjunto fundamental de soluciones de y′′ + y = 0. Entonces
y
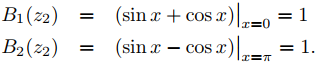
Por lo tanto
B1(z1)B2(z2) − B1(z2)B2(z1) = 2,
entonces el teorema 9.13.1.2 implica que (9.13.1.21) tiene solución única. Sea
y1 = B1(z2)z1 − B1(z1)z2 = cosx − senx
y
y2 = B2(z2)z1 − B2(z1)z2 = cosx + sen x.
Entonces B1(y1) = 0, B2(y2) = 0, y el Wronskiano de {y1, y2} es
Como P0 = 1, (9.13.1.17), ser obtiene solución
La función de Green es
♦
Ahora consideraremos la situación no cubierta por el Teorema 9.13.1.3.
Teorema 9.13.1.4
Supongamos que el problema de valores en la frontera homogéneo
Ly = 0, B1(y) = 0, B2(y) = 0 (9.13.1.22)
tiene una solución no trivial y1, y sea y2 cualquier solución de Ly = 0 que no sea un múltiplo constante de y1. Sea W = y1y2′ − y1′ y2. Si
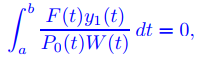(9.13.1.23)
entonces el problema homogéneo de valores en la frontera
Ly = F, B1(y) = 0, B2(y) = 0 (9.13.1.24)
tiene infinitas soluciones, todas de la forma y = yp + c1y1, donde
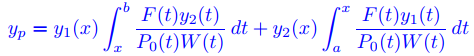
y c1 es una constante. Si
entonces (9.13.1.24) no tiene solución. ♦
Prueba:
De la demostración del Teorema 9.13.1.3, yp es una solución particular de Ly = F, y
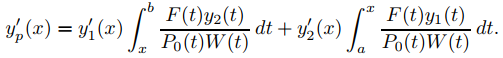
Por tanto, la solución general de (9.13.1.22) es de la forma
y = yp + c1y1 + c2y2,
donde c1 y c2 son constantes. Entonces
Como B1(y1) = 0, el teorema 9.13.1.1 implica que B1(y2) ∕= 0; por tanto, B1(y) = 0 si y sólo si c2 = 0.
Por lo tanto y = yp + c1y1 y
ya que B2(y1) = 0. Del teorema 9.13.1.1, B2(y2) ≠ 0 (ya que B2(y1 = 0). Por lo tanto, Ly = 0 si y solo si (9.13.1.23) se cumple. Esto completa la prueba. ♦
Ejemplo ilustrativo 9.13.1.7
Aplicación del Teorema 9.13.1.4 al problema de valores en la frontera
y′′ + y = F(x), y(0) = 0, y(π) = 0 (9.13.1.25)
explica los Ejemplos 9.13.1.2 y 9.13.1.3. La ecuación complementaria y′′ + y = 0 tiene las soluciones lineales independientes y1 = senx e y2 = cosx, e y1 satisface ambas condiciones de contorno. Como P0 = 1 y
(9.13.1.23) se reduce a
Del ejemplo 9.13.1.2, F(x) = 1 y
entonces el Teorema 9.13.1.3 implica que (9.13.1.25) no tiene solución. En el ejemplo 9.13.1.3,
F(x) = sen2x = 2 senx cosx
y
entonces el Teorema 9.13.1.3 implica que (9.13.1.25) tiene infinitas soluciones, que difieren en múltiplos constantes de y1(x) = senx. ♦