| 9. Ecuaciones diferenciales |

9.8. La transformada de Laplace. Objetivos de aprendizaje:

La SECCIÓN 9.8.2 trata el problema de encontrar una función que tenga una transformada de Laplace dada.
La SECCIÓN 9.8.3 aplica la transformada de Laplace para resolver problemas de valor inicial para ecuaciones diferenciales de segundo orden con coeficientes constantes en (0, ∞).
La SECCIÓN 9.8.4 presenta la función escalón unitario.
La SECCIÓN 9.8.5 usa la función escalón unitario para resolver ecuaciones con coeficientes constantes y con funciones de forzamiento continuas por tramos.
La SECCIÓN 9.8.6 trata del teorema de convolución, una propiedad teórica importante de la transformada de Laplace.
La SECCIÓN 9.8.7 introduce la idea de fuerza impulsiva y trata las ecuaciones con coeficientes constantes con funciones de fuerza impulsiva.
La SECCIÓN 9.8.8 es una breve tabla de transformadas de Laplace.

• Miscelánea de ejercicios resueltos sobre la transformada de Laplace

      EN ESTE CAPÍTULO estudiamos el método de las transformadas de Laplace, el cual ilustra una de las técnicas básicas de resolución de problemas en matemáticas: transformar un problema difícil en uno más sencillo, resolver este último y luego usar su solución para obtener la solución del problema original. El método discutido aquí transforma un problema de valores iniciales para una ecuación de coeficientes constantes en una ecuación algebraica, cuya solución puede luego utilizarse para resolver el problema de valores iniciales dado. En algunos casos, este método es simplemente un procedimiento alternativo para resolver problemas que también pueden resolverse igualmente bien mediante métodos que ya hemos considerado; sin embargo, en otros casos, el método de las transformadas de Laplace es más eficiente que los métodos discutidos anteriormente. Esto es especialmente cierto en problemas físicos que involucran funciones de forzamiento discontinuas.

9.8.1 INTRODUCCIÓN A LA TRANSFORMADA DE LAPLACE

| 9. Ecuaciones diferenciales | 9.8 La transformada de Laplace | Ejercicios propuestos para el Capítulo 9.8.1 |

Definición de la transformada de Laplace

Para definir la transformada de Laplace, primero recordamos la definición de una integral impropia. Si g es una función integrable en el intervalo [a, T] para todo T > a, entonces la integral impropia de g sobre [a, ∞) se define como

             (9.8.1.1)

Decimos que la integral impropia converge si existe el límite en (9.8.1.1); de lo contrario, decimos que la integral impropia diverge o no existe. A continuación presentamos la definición de la transformada de Laplace de una función f.

Definición 9.8.1.1

Sea f una función definida para t ≥ 0 y sea s un número real. Entonces la transformada de Laplace de f es la función F definida por

              (9.8.1.2)

para aquellos valores de s para los que converge la integral impropia.  ♦

 

      Es importante tener en cuenta que la variable de integración en (9.8.1.2) es t, mientras que s es un parámetro independiente de t. Usamos t como la variable independiente para f  debido a que en las aplicaciones la transformada de Laplace generalmente se aplica a funciones que varían en el tiempo.

      La transformada de Laplace puede verse como un operador que transforma la función f = f (t) en la función F = F(s). Por tanto, (9.8.1.2) se puede expresar como

F = (f ).

Las funciones f  y F forman un par de transformadas, que a veces denotaremos por

Se puede demostrar que si F(s) se define para s = s₀, entonces se define para todo s > s₀ (Ejercicio 14 (b)).

Cálculo de algunas transformadas simples de Laplace

Ejemplo ilustrativo 9.8.1.1

Encuentre la transformada de Laplace de f (t) = 1.

Solución:

De (9.8.1.2) con f (t) = 1,

Si s ≠ 0 entonces

        (9.8.1.3)

Por lo tanto

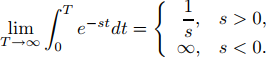        (9.8.1.4)

Si s = 0 el integrando se reduce a la constante 1, y

Por lo tanto, F(0) no está definida y

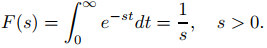
Este resultado se puede escribir en notación de operador como

(1)

o como el par de transformación

♦

OBSERVACIÓN: Es conveniente combinar los pasos de integrar de 0 a T y dejar que T → ∞. Por lo tanto, en lugar de escribir (9.8.1.3) y (9.8.1.4) como pasos separados, escribimos

Seguiremos esta práctica a lo largo de este capítulo.  

Ejemplo ilustrativo 9.8.1.2

Encuentre la transformada de Laplace de f (t) = t.

Solución:

De (9.8.1.2) con f (t) = t,

        (9.8.1.5)

Si s ≠ 0, la integración por partes da como resultado

Si s = 0, la integral en (9.8.1.5) se convierte en

Por lo tanto F(0) es indefinida y

Este resultado también se puede escribir como

(t)

o como el par de transformación

♦

Ejemplo ilustrativo 9.8.1.3

Encuentre la transformada de Laplace de f (t) = e^at, donde a es una constante.

Solución:

Desde (9.8.1.2) con f (t) = e^at,

Combinando las exponenciales, se obtiene

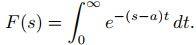
Sin embargo, sabemos por el Ejemplo ilustrativo 9.8.1.1 que

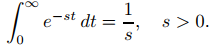
Al sustituir s por s − a, se obtiene

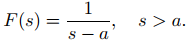
Esto también se puede escribir como

♦

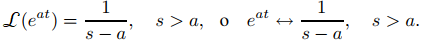Ejemplo ilustrativo 9.8.1.4

Encuentre las transformadas de Laplace de f (t) = senωt  y  g(t) = cosωt, donde ω es una constante.

Solución:

Defina

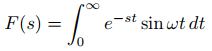      (9.8.1.6)

y

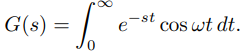      (9.8.1.7)

Si s > 0, integrando (9.8.1.6) por partes se obtiene

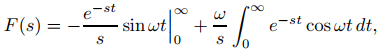
así que

        (9.8.1.8)

Si s > 0, integrando (9.8.1.7) por partes se obtiene

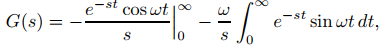
así que

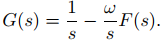
Ahora sustituya F(s) dada en (9.8.1.8) en la fórmula anterior para obtener

Resolviendo esto para G(s) se obtiene

Esto y (9.8.1.8) implican que

♦

Tablas de transformadas de Laplace

Se han compilado extensas tablas de transformadas de Laplace y se usan comúnmente en aplicaciones. La breve tabla de transformadas de Laplace en el Apéndice será adecuada para nuestros propósitos.

Ejemplo ilustrativo 9.8.1.5

Usa la tabla de transformadas de Laplace para encontrar (t³e^4t).

Solución:

La tabla incluye el par de transformación

Establecer n = 3 y a = 4 aquí produce

 

A veces escribimos transformadas de Laplace de funciones específicas sin indicar explícitamente cómo se obtienen. En tales casos, debe consultar la tabla de transformadas de Laplace.

Linealidad de la transformada de Laplace

El siguiente teorema presenta una propiedad importante de la transformada de Laplace.

Teorema 9.8.1.2 Propiedad de linealidad

Suponga que (f_i) se define para s > s_i , 1 ≤ i ≤ n. Sea s₀ el mayor de los números s₁, s₂, . . . , s_n, y sean c₁, c₂ ,. . . , c_n constantes. Entonces

para s > s₀.  ♦

---

Prueba:
Damos la prueba para el caso donde n = 2. Si s > s₀ entonces

♦

Ejemplo ilustrativo 9.8.1.6

Utilice el Teorema 9.8.1.2 y la conocida transformada de Laplace 

para encontrar (cosh bt), (b ≠ 0).

Solución:

Por definición,

Por lo tanto

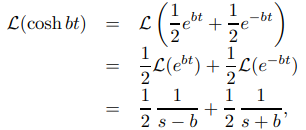    (propiedad de linealidad)       (9.8.1.9)

donde la primera transformada a la derecha se define para s > b y la segunda para s > −b; por tanto, ambos se definen para s > | b |. Simplificar la última expresión en (9.8.1.9) produce

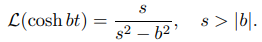
El primer teorema de traslación

El siguiente teorema nos permite comenzar con pares de transformadas conocidos y deducir otros. (Para más resultados de este tipo, véanse los Ejercicios 6 y 13.)

Teorema 9.8.1.3 Primer teorema de traslación

Si

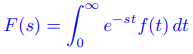      (9.8.1.10)

es la transformada de Laplace de f (t) para s > s₀, entonces F(s − a) es la transformada de Laplace de e^at f (t) para s > s₀ + a. ♦

---

PRUEBA:
Reemplazando s por s − a en (9.8.1.10) produce

        (9.8.1.11)

si s − a > s₀; es decir, si s > s₀ + a. Sin embargo, (9.8.1.11) se puede reescribir como

lo que implica la conclusión del teorema.  

---

 

Ejemplo ilustrativo 9.8.1.7

Utilice el teorema 9.8.1.3 y las transformadas de Laplace conocidas de 1, t, cosωt y senωt para hallar

y

Solución:
En la siguiente tabla, los pares de transformadas conocidas se enumeran a la izquierda y los pares de transformadas requeridos enumerados a la derecha se obtienen aplicando el teorema 9.8.1.3

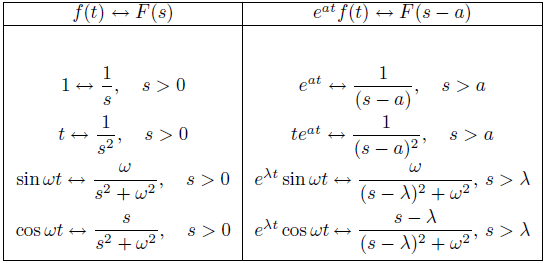
Existencia de transformadas de Laplace

No todas las funciones tienen una transformada de Laplace. Por ejemplo, se puede demostrar (Ejercicio 3) que

para cada número real s. Por tanto, la función no tiene una transformada de Laplace.

      Nuestro próximo objetivo es establecer condiciones que aseguren la existencia de la transformada de Laplace de una función. Primero revisamos algunas definiciones relevantes del cálculo.

Recuerde que un límite

existe si y solo si los límites unilaterales

y 

ambos existen y son iguales; en este caso,

Recuerde también que f es continua en un punto t₀ en un intervalo abierto (a, b) si y sólo si

que es equivalente a

        (9.8.1.12)

Por simplicidad, definimos

  y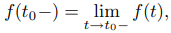 

por lo que (9.8.1.12) se puede expresar como

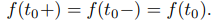
Si y tienen valores finitos pero distintos, decimos que f tiene una discontinuidad de salto en t₀, y

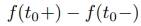
se llama salto en f en t₀ (figura 9.8.1.1).

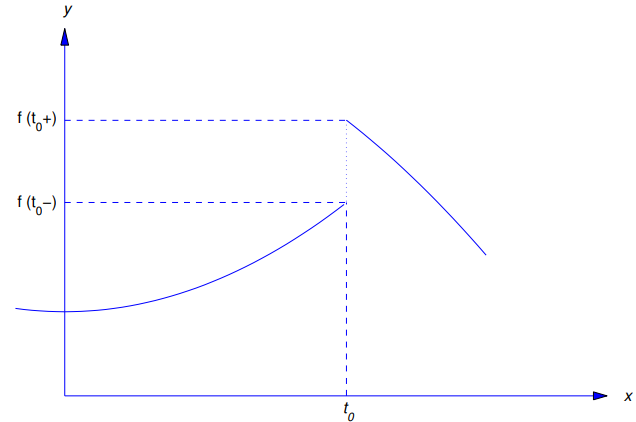
Si y son finitos e iguales, pero f no está definida en t₀ o está definida pero

decimos que f tiene una discontinuidad removible en t₀ (Figura 9.8.1.2).

(Figura 9.8.1.2)

Esta terminología es apropiada ya que una función f con una discontinuidad removible en t₀ puede hacerse continua en t₀ definiendo (o redefiniendo)

OBSERVACIÓN: Sabemos por cálculo que una integral definida no se ve afectada al cambiar los valores de su integrando en puntos aislados. Por lo tanto, redefinir una función f para hacerla continua en discontinuidades removibles no cambia ( f ).

Definición 9.8.1.4

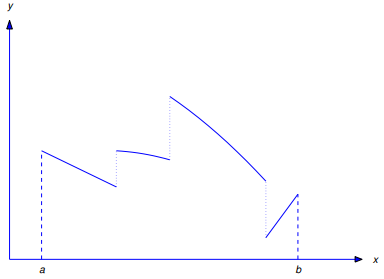
(i) Se dice que una función f es continua por tramos en un intervalo cerrado finito [0, T] si f (0+) y f (T−) son finitas y f es continua en el intervalo abierto (0, T) excepto posiblemente en un número finito de puntos, donde f puede tener discontinuidades de salto o discontinuidades removibles.
(ii) Se dice que una función f es continua por tramos en el intervalo infinito [0, ∞) si es continua por tramos en [0, T] para cada T > 0.  ♦

 

La figura 9.8.1.3 muestra la gráfica de una función continua por tramos típica

      En cálculo se muestra que si una función es continua por tramos en un intervalo cerrado finito, entonces es integrable en ese intervalo. Pero si  f  es continua por tramos en [0, ∞), entonces también lo es e^{− st} f (t), y por lo tanto

existe para cada T > 0. Sin embargo, la continuidad por tramos por sí sola no garantiza que la integral impropia

        (9.8.1.13)

converge para s en algún intervalo (s₀ , ∞). Por ejemplo, notamos anteriormente que (9.8.1.13) diverge para todos los s si . Dicho de manera informal, esto ocurre porque aumenta demasiado rápido cuando t → ∞. La siguiente definición proporciona una restricción sobre el crecimiento de una función que garantiza la convergencia de su transformada de Laplace para s en algún intervalo (s₀ , ∞).

Definición 9.8.1.5

Se dice que una función f es de orden exponencial s₀ si hay constantes M y t₀ tales que

        (9.8.1.14)

En situaciones donde el valor específico de s₀ es irrelevante, decimos simplemente que f es de orden exponencial. ♦

     

       El siguiente teorema proporciona condiciones suficientes útiles para que una función f tenga una transformada de Laplace. La demostración se bosqueja en el Ejercicio 10.

Teorema 9.8.1.6

Si f es continua por tramos en [0, ∞) y de orden exponencial s₀, entonces ( f ) se define para s > s₀.  ♦

OBSERVACIÓN: Enfatizamos que las condiciones del Teorema 9.8.1.6 son suficientes, pero no necesarias, para que f tenga una transformada de Laplace. Por ejemplo, el Ejercicio 14 (c) muestra que f puede tener una transformada de Laplace aunque f no sea de orden exponencial.

Ejemplo ilustrativo 9.8.1.8

Si f está acotada en algún intervalo [t₀, ∞), digamos

| f (t) | ≤  M,  t  ≥  t₀,

entonces (9.8.1.14) se cumple con s₀ = 0, entonces f es de orden exponencial cero. Así, por ejemplo, senωt  y  cosωt  son de orden exponencial cero, y el Teorema 9.8.1.6 implica que (senωt)  y  (cosωt) existen para s > 0. Esto es consistente con la conclusión del Ejemplo 9.8.1.4

Ejemplo ilustrativo 9.8.1.9

Se puede demostrar que si existe y es finito, entonces f es de orden exponencial s₀ (Ejercicio 9). Si α es cualquier número real y s₀ > 0 entonces f (t) = t^α es de orden exponencial s₀, ya que

por la regla de L’Hôpital. Si α ≥ 0, f también es continua en [0, ∞). Por lo tanto, el Ejercicio 9 y el Teorema 9.8.1.6 implican que (t ^α) existe para s ≥ s₀. Sin embargo, dado que s₀ es un número positivo arbitrario, esto realmente implica que (t ^α) existe para todo s > 0. Esto es consistente con los resultados del Ejemplo 9.8.1.2 y los Ejercicios 6 y 8.

Ejemplo ilustrativo 9.8.1.10

Encuentre la transformada de Laplace de la función continua por tramos

Solución:

Dado que f está definida por diferentes fórmulas en [0, 1) y [1, ∞), escribimos

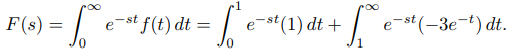
Ya que

y

resulta que

Esto es consistente con el Teorema 9.8.1.6, ya que

y por lo tanto f es de orden exponencial s₀ = −1.

OBSERVACIÓN: En la Sección 9.8.4 desarrollaremos un método más eficiente para encontrar transformadas de Laplace de funciones continuas por tramos.

Ejemplo ilustrativo 9.8.1.11

Nosotros dijimos anteriormente que

Para todas las s, por lo que el Teorema 9.8.1.6 implica que no es de orden exponencial, ya que

así que

para valores suficientemente grandes de t, para cualquier elección de M y s₀ (Ejercicio 3).