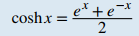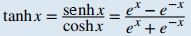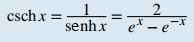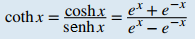| 1. Funciones y sus gráficas | 1.5 Funciones exponenciales y logarítmicas | Ejercicios propuestos del Capítulo 1.5 |
Funciones hiperbólicas
Las funciones hiperbólicas se definen en términos de ciertas combinaciones de eˣ y e⁻ˣ. Estas funciones surgen naturalmente en diversas aplicaciones de ingeniería y física, incluido el estudio de las ondas de agua y las vibraciones de las membranas elásticas. Otro uso común para una función hiperbólica es la representación de una cadena o cable colgante, también conocida como catenaria (Figura 1.5_6). Si introducimos un sistema de coordenadas para que el punto bajo de la cadena se encuentre a lo largo del eje y, podemos describir la altura de la cadena en términos de una función hiperbólica. Primero, definimos las funciones hiperbólicas.

(Figura 1.5_6 La forma de un hilo de seda en una telaraña se puede describir en términos de una función hiperbólica. La misma forma se aplica a una cadena o cable que cuelga de dos soportes con sólo su propio peso. (crédito: “Mtpaley”, Wikimedia Commons))
DEFINICIÓN 1.5_1. Funciones hiperbólicas
|
Coseno hiperbólico Seno hiperbólico Tangente hiperbólica Cosecante hiperbólica Secante hiperbólica Cotangente hiperbólica |
Utilizando la definición de cosh(x) y los principios de la física, se puede demostrar que la altura de una cadena colgante, como la de la figura 1.5_6, se puede describir mediante la función h(x) = acosh (x/a) + c para ciertas constantes a y c.
Pero, ¿por qué estas funciones se llaman funciones hiperbólicas? Para responder a esta pregunta, considere la cantidad cosh²t − senh²t. Usando la definición de cosh y senh, vemos que

Esta identidad es análoga a la identidad trigonométrica cos²t + sen²t = 1. Aquí, dado un valor t, el punto (x, y) = (cosht, senht) se encuentra en la hipérbola unitaria x² − y² = 1 (Figura 1.5_7).

Gráficas de las funciones hiperbólicas
Para graficar coshx y senhx, utilizamos el hecho de que ambas funciones se aproximan a (1/2)eˣ cuando x → ∞, ya que e⁻ˣ → 0 cuando x → ∞. Cuando x → −∞, coshx se acerca a (1/2)e⁻ˣ, mientras que senhx se acerca a −(1/2)e⁻ˣ. Por lo tanto, usando las gráficas de (1/2)eˣ, (1/2)e⁻ˣ y −(1/2)e⁻ˣ como guías, graficamos coshx y senhx. Para graficar tanhx, usamos el hecho de que tanh (0) = 0, −1 < tanh(x) < 1 para todo x, tanhx → 1 cuando x → ∞, y tanhx → −1 cuando x → −∞. Las gráficas de las otras tres funciones hiperbólicas se pueden dibujar utilizando las gráficas de coshx, senhx y tanhx (Figura 1.5_8).

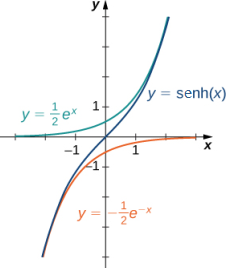




(Figura 1.5_8 Las funciones hiperbólicas implican combinaciones de eˣ y e⁻ˣ.)
Identidades que implican funciones hiperbólicas
La identidad cosh²t − senh²t = 1, que se muestra en la Figura 1.5_7, es una de varias identidades que involucran las funciones hiperbólicas, algunas de las cuales se enumeran a continuación. Las primeras cuatro propiedades se deducen fácilmente de las definiciones de seno hiperbólico y coseno hiperbólico. Excepto por algunas diferencias en los signos, la mayoría de estas propiedades son análogas a las identidades para las funciones trigonométricas.
REGLA 1.5.4: IDENTIDADES QUE INCLUYEN FUNCIONES HIPERBÓLICAS
| 1. cosh (−x) = coshx 2. senh (−x) = – senhx 3. coshx + senhx = eˣ 4. coshx − senhx = e⁻ˣ 5. cosh²x − senh²x = 1 6. 1 − tanh²x = sech²x 7. coth²x − 1 = csch²x 8. senh (x ± y) = senhxcoshy ± coshxsenhy 9. cosh (x ± y) = coshxcoshy ± sinhxsenhy |
Ejemplo ilustrativo 1.5_8 Evaluación de funciones hiperbólicas
- Simplifica senh(5lnx).
- Si senhx = 3/4, encuentre los valores de las cinco funciones hiperbólicas restantes.
Solución:
a. Usando la definición de la función senh, escribimos

b. Usando la identidad cosh²x − senh²x = 1, vemos que

Como coshx ≥ 1 para todo x, debemos tener coshx = 5/4. Luego, usando las definiciones para las otras funciones hiperbólicas, concluimos que tanhx = 3/5, cschx = 4/3, sechx = 4/5 y cothx = 5/3. ◊
EJERCICIO DE CONTROL 1.5_8
Simplifica cosh(2lnx).
Funciones hiperbólicas inversas
A partir de las gráficas de las funciones hiperbólicas, vemos que todas ellas son uno a uno, excepto coshx y sechx. Si restringimos los dominios de estas dos funciones al intervalo [0, ∞), entonces todas las funciones hiperbólicas son uno a uno, y podemos definir las funciones hiperbólicas inversas. Dado que las funciones hiperbólicas en sí mismas implican funciones exponenciales, las funciones hiperbólicas inversas involucran funciones logarítmicas.
DEFINICIÓN. Funciones hiperbólicas inversas


Veamos cómo deducir la primera ecuación. Las otras se deducen de manera similar. Supongamos que y = senh⁻¹x. Entonces, x = senhy y, por la definición de la función seno hiperbólica,

Por lo tanto,

Multiplicando esta ecuación por eʸ, obtenemos

Esto se puede resolver como una ecuación cuadrática, con la solución

Como eʸ > 0, la única solución es la que tiene el signo positivo. Aplicando el logaritmo natural a ambos lados de la ecuación, concluimos que

Ejemplo ilustrativo 1.5_9 Evaluación de funciones hiperbólicas inversas
Evalúa cada una de las siguientes expresiones.
a. senh⁻¹ (2)
b. tanh⁻¹ (1/4)
Solución:

EJERCICIO DE CONTROL 1.5_9
Evalúe tanh⁻¹ (1/2).