9.2. Ecuaciones diferenciales de primer orden

9.2 Ecuaciones diferenciales de primer orden: Objetivos de aprendizaje

En este CAPÍTULO 9.2 Estudiamos ecuaciones diferenciales de primer orden para las cuales existen métodos generales de solución.

LA SECCIÓN 9.2.1 Trata de ecuaciones lineales, el tipo más simple de ecuaciones de primer orden. En esta sección presentamos el método de variación de parámetros. La idea subyacente a este método será un tema unificador de nuestro enfoque para resolver muchos tipos diferentes de ecuaciones diferenciales a lo largo del capítulo.

La SECCIÓN 9.2.2 Trata con ecuaciones separables, las ecuaciones no lineales más simples. En esta sección presentamos la idea de soluciones implícitas y constantes de ecuaciones diferenciales, y señalamos algunas diferencias entre las propiedades de las ecuaciones lineales y no lineales.

La SECCIÓN 9.2.3 Discute la existencia y la unicidad de soluciones de ecuaciones no lineales. Aunque puede parecer lógico colocar esta sección antes de la Sección 9.2.2, presentamos la Sección 9.2.2 primero para que podamos tener ejemplos ilustrativos en la Sección 9.2.3.

La SECCIÓN 9.2.4 Trata ecuaciones no lineales que no son separables, pero que pueden transformarse en ecuaciones separables mediante un procedimiento similar a la variación de parámetros.

La SECCIÓN 9.2.5 Cubre ecuaciones diferenciales exactas, que reciben este nombre porque el método para resolverlas utiliza la idea de una diferencial exacta del cálculo.

La SECCIÓN 9.2.6 Trata ecuaciones que no son exactas, pero que pueden hacerse exactas multiplicándolas por una función conocida llamada factor integrador.

9.2.1 ECUACIONES LINEALES DE PRIMER ORDEN

Se dice que una ecuación diferencial de primer orden es lineal si se puede escribir como

y′ + p(x)y = f (x). (9.2.1_1)

Una ecuación diferencial de primer orden que no se puede escribir así es no lineal. Decimos que (9.2.1_1) es homogénea si f ≡ 0; de lo contrario es no homogénea. Dado que y ≡ 0 es obviamente una solución de la ecuación homogénea

y′ + p(x)y = 0,

la llamamos la solución trivial. Cualquier otra solución es no trivial.

Ejemplo ilustrativo 9.2.1_1

Las ecuaciones de primer orden

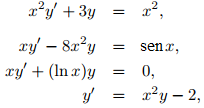
no tienen la forma (9.2.1_1), pero son lineales, ya que pueden reescribirse como

Ejemplo ilustrativo 9.2.1_2

Aquí hay tres ecuaciones no lineales de primer orden:

xy′ + 3y² = 2x	(porque y está al cuadrado),
yy′ = 3	(debido al producto yy′),
y′ + xeʸ = 12	(debido al factor eʸ).

Solución general de una ecuación diferencial lineal de primer orden

Para motivar una definición que necesitaremos, considere la ecuación lineal simple de primer orden

Por cálculo sabemos que y satisface esta ecuación si y sólo si

donde c es una constante arbitraria. Llamamos a c un parámetro y decimos que (9.2.1_3) define una familia de funciones uniparamétrica (con un parámetro). Para cada número real c, la función definida por (9.2.1_3) es una solución de (9.2.1_2) en (−∞, 0) y (0, ∞); además, cada solución de (9.2.1_2) en cualquiera de estos intervalos tiene la forma (9.2.1_3) para alguna elección de c. Decimos que (9.2.1_3) es la solución general de (9.2.1_2).

Veremos que ocurre una situación similar en relación con cualquier ecuación lineal de primer orden

y′ + p(x)y = f (x); (9.2.1_4)

es decir, si p y f son continuas en algún intervalo abierto (a, b), entonces hay una fórmula única y = y(x, c) análoga a (9.2.1_3) que involucra x y un parámetro c y tiene las siguientes propiedades:

Para cada valor fijo de c, la función resultante en la variable x es una solución de (9.2.1_4) en (a, b).
Si y es una solución de (9.2.1_4) en (a, b), entonces se puede obtener y de la fórmula eligiendo c apropiadamente.

Llamaremos a y = y(x, c) la solución general de la ED (9.2.1_4).

Cuando esto se haya establecido, se deducirá que una ecuación de la forma

tiene una solución general en cualquier intervalo abierto (a, b) en el que P₀, P₁ y F son continuos y P₀ no tiene ceros, ya que en este caso podemos reescribir (9.2.1_5) en la forma (9.2.1_4) con p = P₁/P₀ y f = F/P₀, que son continuas en (a, b).

Para evitar una redacción incómoda en ejemplos y ejercicios, no especificaremos el intervalo (a, b) cuando solicitemos la solución general de una ecuación lineal específica de primer orden. Acordemos que esto siempre significa que queremos la solución general en cada intervalo abierto en el que p y f son continuas si la ecuación es de la forma (9.2.1_4), o en la que P₀, P₁ y F son continuos y P₀ es distinta de cero, si la ecuación es de la forma (9.2.1_5). Dejamos que identifique estos intervalos en ejemplos y ejercicios específicos.

Para completar, señalamos que si P₀, P₁ y F son continuos en un intervalo abierto (a, b), pero P₀ tiene un cero en (a, b), entonces (9.2.1_5) puede no tener una solución general en (a, b) en el sentido recién definido. Como este no es un punto importante que deba desarrollarse en profundidad, no lo discutiremos más a fondo; sin embargo, vea el Ejercicio 9.2.1_44 para un ejemplo.

Ecuaciones lineales homogéneas de primer orden

Comenzamos con el problema de encontrar la solución general de una ecuación lineal homogénea de primer orden. El siguiente ejemplo recuerda un resultado familiar del cálculo.

Ejemplo ilustrativo 9.2.1_3

Sea a una constante

(a) Encuentre la solución general de

y′ − ay = 0. (9.2.1_6)

(b) Resuelva el problema de valor inicial

y′ − ay = 0, y(x₀) = y₀.

Solución:

(a) Usted ya sabe por cálculo que si c es alguna constante, entonces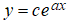satisface (9.2.1_6).

Sin embargo, supongamos que ha olvidado esto y utilizamos este problema para ilustrar un método general para resolver una ecuación lineal homogénea de primer orden.

Sabemos que (9.2.1_6) tiene la solución trivial y ≡ 0. Ahora supongamos que y es una solución no trivial de (9.2.1_6). Entonces, dado que una función diferenciable debe ser continua, debe haber algún intervalo abierto I en el que y no tenga ceros. Reescribimos (9.2.1_6)) como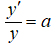

para x en I. La integración de esta ecuación muestra que

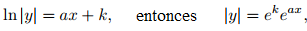
donde k es una constante arbitraria. Como eᵃˣ nunca puede ser igual a cero, y no tiene ceros, entonces y es siempre positivo o siempre negativo. Por lo tanto, podemos reescribir y como

donde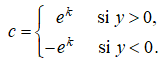

Esto muestra que cada solución no trivial de (9.2.1_6) tiene la forma y = ceᵃˣ para alguna constante no nula c. Como establecer c = 0 produce la solución trivial, todas las soluciones de (9.2.1_6) tienen la forma (9.2.1_7). De igual forma, se tiene que (9.2.1_7) es una solución de (9.2.1_6) para cada elección de c, ya que diferenciar (9.2.1_7) produce y′ = aceᵃˣ = ay.

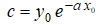(b) Imponer la condición inicial y(x₀) = y₀ produceentoncesy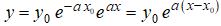

La Figura 9.2.1_1 muestra las gráficas de esta función con x₀ = 0, y₀ = 1 y varios valores de a.

**Figura 9.2.1_1** Soluciones de y′ − ay = 0, y(0) = 1

Ejemplo ilustrativo 9.2.1_4

(a) Encuentre la solución general de

xy′ + y = 0. (9.2.1_8)

(b) Resuelva el problema de valor inicial

xy′ + y = 0, y(1) = 3. (9.2.1_9)

Solución:

(a) Reescribimos (9.2.1_8) como

donde x está restringido a (−∞, 0) o (0, ∞). Si y es una solución no trivial de (9.2.1_10), debe haber algún intervalo abierto I en el que y no tenga ceros. Podemos reescribir (9.2.1_10) como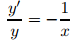para x en I. La integración muestra que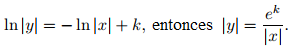Como una función que satisface la última ecuación no puede cambiar el signo en (−∞, 0) o (0, ∞), podemos reescribir este resultado de manera más simple comodonde

Ahora hemos demostrado que cada solución de (9.2.1_10) viene dada por (9.2.1_11) para algunas opciones de c. (Aunque asumimos que y no era trivial para deducir (9.2.1_11), podemos obtener la solución trivial estableciendo c = 0 en (9.2.1_11).) Recíprocamente, cualquier función de la forma (9.2.1_11) es un solución de (9.2.1_10), ya que diferenciar (9.2.1_11) producey, al sustituir la ecuación anterior y la función (9.2.1_11) en (9.2.1_10), se obtiene

La figura 9.2.1_2 muestra las gráficas de algunas soluciones correspondientes a varios valores de c:

**Figura 9.2.1_2** Soluciones de xy′ + y = 0 en (0, ∞) y (−∞, 0)

(b) La imposición de la condición inicial y(1) = 3 en (9.2.1_11) produce c = 3. Por lo tanto, la solución de (9.2.1_9) es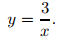El intervalo de validez de esta solución es (0, ∞).

Los resultados en los ejemplos 9.2.1_3 (a) y 9.2.1_4 (b) son casos especiales del siguiente teorema.

Teorema 9.2.1.1. Solución general de la ED lineal homogénea de primer orden

Si p es continua en un intervalo abierto (a, b), entonces la solución general de la ecuación homogénea

y′ + p(x)y = 0 (9.2.1_12)

en (a, b) es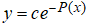donde

P(x) = ∫p(x)dx (9.2.1_13)

es cualquier antiderivada de p en (a, b); es decir,

P′(x) = p(x), a < x < b. (9.2.1_14) ♦

Prueba:

Si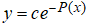al diferenciar y y usar (9.2.1_14), se obtieneentonces y′ + p(x)y = 0; es decir, y es una solución de (9.2.1_12), para cualquier elección de c.

Ahora mostraremos que cualquier solución de (9.2.1_12) se puede escribir como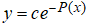para alguna constante c. La solución trivial se puede obtener de esta manera, con c = 0. Ahora suponga que y es una solución no trivial. Luego hay un subintervalo abierto I de (a, b) en el que y no tiene ceros. Podemos reescribir (9.2.1_12) comopara x en I. Integrando (9.2.1_15) y teniendo presente (9.2.1_13) obtenemos

ln|y| = −P(x) + k,

donde k es una constante Esto implica queComo P se define para todas las x en (a, b) y una exponencial nunca puede ser igual a cero, podemos tomar I = (a, b), de tal modo que y no tiene ceros en (a, b), y se puede reescribir la última ecuación como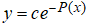 donde◊

OBSERVACIÓN: Reescribir una ecuación diferencial de primer orden para que un lado dependa solo de y e y′ y el otro dependa solo de x se llama separación de variables. Hicimos esto en los Ejemplos 9.2.1_3 y 9.2.1_4, y al reescribir (9.2.1_12) como (9.2.1_15). Aplicaremos este método a ecuaciones no lineales en la Sección 9.2.2.

Ecuaciones lineales no homogéneas de primer orden

Ahora resolveremos la ecuación no homogénea

y′ + p(x)y = f (x). (9.2.1_16)

Al considerar esta ecuación llamamos a

y′ + p(x)y = 0

la ecuación complementaria.

Encontraremos soluciones de (9.2.1_16) en la forma y = uy₁, donde y₁ es una solución no trivial de la ecuación complementaria y u debe determinarse. Este método de usar una solución de la ecuación complementaria para obtener soluciones de una ecuación no homogénea es un caso especial de un método llamado variación de parámetros, que encontrará varias veces en este capítulo. (Obviamente, u no puede ser constante, ya que si lo fuera, el lado izquierdo de (9.2.1_16) sería cero. Reconociendo esto, los primeros usuarios de este método lo vieron como un “parámetro” que varía; de ahí, el nombre “variación de parámetros”.)

y = uy₁, entonces y′ = u′y₁ + uy′₁.

Sustituyendo estas expresiones por y y y′ en (9.2.1_16) obtenemos

u′y₁ + u(y′₁ + p(x)y₁) = f (x),

que se reduce a

u′y₁ = f (x), (9.2.1_17)

ya que y₁ es una solución de la ecuación complementaria; es decir,

y′₁ + p(x)y₁ = 0.

En la demostración del Teorema 9.2.2_1 vimos que y₁ no tiene ceros en un intervalo donde p es continua. Por lo tanto, podemos dividir (9.2.1_.17) entre y₁ para obtener

Podemos integrar la ED anterior (introduciendo una constante de integración) y multiplicar el resultado por y₁ para obtener la solución general de (9.2.1_16). Antes de pasar a la prueba formal de este hecho, consideremos algunos ejemplos.

Ejemplo ilustrativo 9.2.1_5

Encuentre la solución general de

Al aplicar (a) del Ejemplo 9.2.1_3 con a = −2, vemos quees una solución de la ecuación complementaria y′ + 2y = 0. Por lo tanto, buscamos soluciones de (9.2.1_18) que presenten la formade tal modo que

Por lo tanto, y es una solución de (9.2.1_18) si y sólo si

entonces

u′ = x³.

Por lo tanto

u = x⁴/4 + c,

es la solución general de (9.2.1_18).

La figura 9.2.1_3 muestra un campo direccional y algunas curvas integrales para (9.2.1_18).

**Figura 9.2.1_3** Un campo direccional y curvas integrales para

Esta imagen tiene un atributo ALT vacío; su nombre de archivo es image-10.png — **Figura 9.2.1_3** Un campo direccional y curvas integrales para

Ejemplo ilustrativo 9.2.1_6

(a) Encuentre la solución general de

(b) Resuelva el problema de valor inicial

y′ + (cotx) y = xcscx, y(π/2) = 1. (9.2.1_21)

Solución:

(a) Aquí p(x) = cotx y f (x) = xcscx son continuas, excepto en los puntos x = rπ, donde r es un número entero. Por lo tanto, buscamos soluciones de (9.2.1_20) en los intervalos (rπ, (r + 1)π). Necesitamos una solución no trivial y₁ de la ecuación complementaria; por lo tanto, y₁ debe satisfacer y′₁ + (cotx)y₁ = 0, que reescribimos como

Integrando, se obtiene

ln|y₁| = − ln|senx|,

donde tomamos la constante de integración como cero ya que solo necesitamos una función que satisfaga (9.2.1_22).
Claramente, y₁ = 1/senx es una opción adecuada. Por lo tanto, buscamos soluciones de (9.2.1_20) en la forma

y = u/senx,

de tal manera que

Por lo tanto, y es una solución de (9.2.1_20) si y sólo si

u′/senx = xcscx = x/senx o, equivalentemente, u′ = x.

Integrando, se obtiene

u = x²/2 + c,

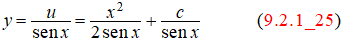
es la solución general de (9.2.1_20) en cada intervalo (rπ, (r + 1)π) (r = entero).

(b) La imposición de la condición inicial y(π/2) = 1 en (9.2.1_25) da como resultado

Así,

es una solución de (9.2.1_21). El intervalo de validez de esta solución es (0, π); La figura 9.2.1_4 muestra su gráfica.

**Figura 9.2.1_4** Solución de y′ + (cotx)y = xcscx, y(π/2) = 1.

OBSERVACIÓN: No era necesario hacer los cálculos (9.2.1_23) y (9.2.1_24) en el Ejemplo ilustrativo 9.2.1_6, ya que en la discusión anterior al ejemplo 9.2.1_5 se mostró que si y = uy₁ donde y′₁ + p(x)y₁ = 0, entonces y′ + p(x)y = u′y₁. Hicimos estos cálculos para que veas que esto sucede en este ejemplo específico. Le recomendamos que incluya estos cálculos “innecesarios” al hacer ejercicios, hasta que esté seguro de que realmente comprende el método. Después de eso, omítalos.

Procedimiento. Variación de parámetros

Resumimos el método de variación de parámetros para resolver

y′ + p(x)y = f (x) (9.2.1_26)

como sigue:

(a) Encuentre una función y₁ tal que

Por conveniencia, tome la constante de integración como cero.

(b) Escriba

y = uy₁ (9.2.1_27)

para recordarte a ti mismo lo que estás haciendo.

(d) Integre u′ para obtener u, con una constante arbitraria de integración.

(e) Sustituya u en (9.2.1_27) para obtener y.

Para resolver una ecuación escrita como

le recomendamos que divida entre P₀(x) para obtener una ecuación de la forma (9.2.1_26) y luego siga el procedimiento anterior.

Soluciones en forma integral

A veces, las integrales que surgen al resolver una ecuación lineal de primer orden no se pueden evaluar en términos de funciones elementales. En este caso, la solución debe dejarse en términos de una integral.

Ejemplo ilustrativo 9.2.1_7

(a) Encuentre la solución general de

y′ − 2xy = 1.

(b) Resuelva el problema del valor inicial

y′ − 2xy = 1, y(0) = y₀. (9.2.1_28)

Solución:

(a) Para aplicar la variación de parámetros, necesitamos una solución no trivial y₁ de la ecuación complementaria; así, y′₁ − 2xy₁ = 0, que reescribimos como

Integrando la ecuación anterior y tomando la constante de integración como cero, se obtiene

Tomamos

y buscamos soluciones de (9.2.1_28) de la forma

donde

Por lo tanto

pero no podemos simplificar la integral a la derecha porque no hay una función elemental con derivada igual a

Por lo tanto, la mejor forma disponible para la solución general de (9.2.1_28) es

(b) Como la condición inicial en (9.2.1_28) se impone en x₀ = 0, es conveniente reescribir (9.2.1_29) como

ya que

Establecer x = 0 e y = y₀ aquí muestra que c = y₀. Por lo tanto, la solución del problema de valor inicial es

Para un valor dado de y₀ y cada x fijo, la integral de la derecha se puede evaluar por métodos numéricos.
Un procedimiento alternativo es aplicar los procedimientos de integración numérica discutidos en el Capítulo 9.3 directamente al problema del valor inicial (9.2.1_28). La figura 9.2.1_5 muestra gráficas de (9.2.1_30) para varios valores de y₀.

**Figura 9.2.1_5** Soluciones de y′ − 2xy = 1, y(0) = y₀

Un teorema de existencia y unicidad

El método de variación de parámetros conduce al siguiente teorema.

Teorema 9.2.1.2. Existencia y unicidad

Suponga que p y f son continuas en un intervalo abierto (a, b), y que y₁ es cualquier solución no trivial de la ecuación complementaria

y′ + p(x)y = 0

en (a, b). Entonces:

(a) La solución general de la ecuación no homogénea

y′ + p(x)y = f (x) (9.2.1_31)

en (a, b) es

y = y₁(x) (c + ∫ f (x)/y₁(x) dx) (9.2.1_32)

(b) Si x₀ es un punto arbitrario en (a, b) e y₀ es un número real arbitrario, entonces el problema del valor inicial

y₀ + p(x)y = f (x), y(x₀) = y₀

tiene la solución única

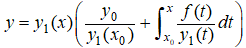
en (a, b). ♦

Prueba:

(a) Para demostrar que (9.2.1_32) es la solución general de (9.2.1_31) en (a, b), debemos demostrar que:

(i) Si c es cualquier constante, la función y en (9.2.1_32) es una solución de (9.2.1_31) en (a, b).
(ii) Si y es una solución de (9.2.1_31) en (a, b) entonces y es de la forma (9.2.1_32) para alguna constante c.

Para demostrar (i), primero observamos que cualquier función de la forma (9.2.1_32) se define en (a, b), ya que p y f son continuas en (a, b). Al diferenciar (9.2.1_32), se obtiene

Dado que y′₁ = −p(x)y₁, esto y (9.2.1_32) implican que

lo que implica que y es una solución de (9.2.1_31).

Para demostrar (ii), suponga que y es una solución de (9.2.1_31) en (a, b). De la demostración del teorema 9.2.1.1, sabemos que y₁ no tiene ceros en (a, b), por lo que la función u = y/y₁ se define en (a, b). Además, dado que

Integrando u′ = f /y₁, obtenemos

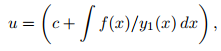
lo que implica (9.2.1_32), ya que y = uy₁.

(b) Hemos probado (a), donde ∫ f(x)/y₁(x) dx en (9.2.1_32) es una antiderivada arbitraria de f /y₁. Ahora es conveniente elegir la antiderivada que es igual a cero cuando x = x₀ y escribir la solución general de (9.2.1_31) como

Ya que

vemos que y(x₀) = y₀ si y sólo si c = y₀/y₁(x₀). ♦

Páginas: 1 2