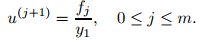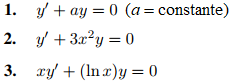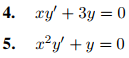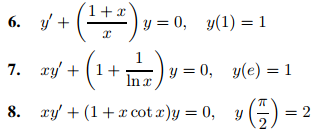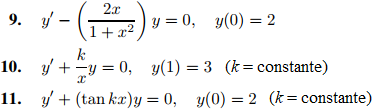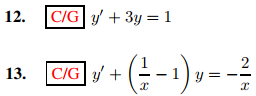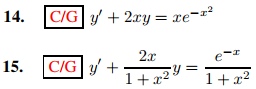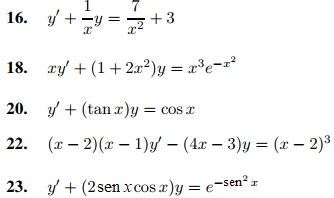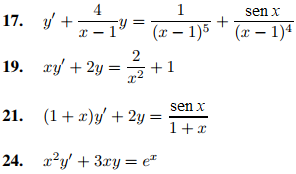| 9. Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden | 9.2.1 Ecuaciones lineales de primer orden |
EJERCICIOS PROPUESTOS DEL CAPÍTULO 9.2.1
En los ejercicios 1 a 5 encuentre la solución general.
En los ejercicios 6 a 11 resuelva el problema de valor inicial dado.
En los ejercicios 12 a 15 encuentre la solución general. Además, trace un campo direccional y algunas curvas integrales en la región rectangular {−2 ≤ x ≤ 2, −2 ≤ y ≤ 2}.
En los ejercicios 16 a 24 encuentre la solución general.
En los ejercicios 25 a 29 resuelva el problema del valor inicial y dibuje la gráfica de la solución.

En los ejercicios 30 a 37 resuelva el problema de valor inicial.

En los ejercicios 38 a 42, resuelva el problema de valor inicial y deje la respuesta en una forma que implique una integral definida. (Puede resolver estos problemas numéricamente mediante los métodos discutidos en el Capítulo 9.3.)

43. Los experimentos indican que el cuerpo absorbe la glucosa a una velocidad proporcional a la cantidad de glucosa presente en el torrente sanguíneo. Deje λ denotar la constante (positiva) de proporcionalidad. Ahora suponga que se inyecta glucosa en el torrente sanguíneo de un paciente a una velocidad constante de r unidades por unidad de tiempo. Sea G = G(t) el número de unidades en el torrente sanguíneo del paciente en el tiempo t > 0. Luego
G′ = −λG + r,
donde el primer término a la derecha se debe a la absorción de glucosa por el cuerpo del paciente y el segundo término se debe a la inyección. Determine G para t > 0, dado que G(0) = G₀. Además, encuentre limt → ∞ G(t).
44. (a) Trace un campo direccional y algunas curvas integrales para
xy′ − 2y = −1 (A)
en la región rectangular {−1 ≤ x ≤ 1, −0.5 ≤ y ≤ 1.5}. ¿Qué tienen en común todas las curvas integrales?
(b) Muestre que la solución general de (A) en (−∞, 0) y (0, ∞) es
y = 1/2 + cx².
(c) Demuestre que y es una solución de (A) en (−∞, ∞) si y sólo si
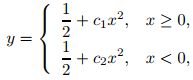
donde c₁ y c₂ son constantes arbitrarias.
(d) Concluya de (c) que todas las soluciones de (A) en (−∞, ∞) son soluciones del problema de valor inicial
xy′ − 2y = −1, y(0) = 1/2.
(e) Use (b) para mostrar que si x₀ ≠ 0 e y₀ es arbitrario, entonces el problema de valor inicial
xy′ − 2y = −1, y(x₀) = y₀
tiene infinitas soluciones en (−∞, ∞). Explique por qué esto no contradice el Teorema 9.2.1.2(b).
45. Suponga que f es una función continua en un intervalo abierto (a, b) y α es una constante.
(a) Deduzca una fórmula para la solución del problema de valor inicial
y′ + αy = f (x), y(x₀) = y₀, (A)
donde x₀ está en (a, b) e y₀ es un número real arbitrario.
(b) Suponga que (a, b) = (a, ∞), α > 0 y limx → ∞ f (x) = L. Demuestre que si y es la solución de (A), entonces limx → ∞ y(x) = L/α.
46. Suponga que todas las funciones en este ejercicio se definen en un intervalo común (a, b).
(a) Demuestre: si y₁ e y₂ son soluciones de
y′ + p(x)y = f₁(x)
y
y′ + p(x)y = f₂(x)
respectivamente, y c₁ y c₂ son constantes, entonces y = c₁y₁ + c₂y₂ es una solución de
y′ + p(x)y = c₁f₁(x) + c₂f₂(x).
(Este es el principio de superposición).
(b) Use (a) para mostrar que si y₁ e y₂ son soluciones de la ecuación no homogénea
y′ + p(x)y = f (x), (A)
entonces y₁ − y₂ es una solución de la ecuación homogénea
y′ + p(x)y = 0. (B)
(c) Use (a) para mostrar que si y₁ es una solución de (A) e y₂ es una solución de (B), entonces y₁ + y₂ es una solución de (A).
47. Algunas ecuaciones no lineales se pueden transformar en ecuaciones lineales cambiando la variable dependiente. Demuestra que si
g′(y)y′ + p(x)g(y) = f (x)
donde y es una función de x y g es una función de y, entonces la nueva variable dependiente z = g(y) satisface la ecuación lineal
z′ + p(x)z = f (x).
48. Resuelva las siguientes ED por el método discutido en el ejercicio 47:


49. Hemos demostrado que si p y f son funciones continuas en (a, b), entonces cada solución de
y′ + p(x)y = f (x) (A)
en (a, b) se puede escribir como y = uy₁, donde y₁ es una solución no trivial de la ecuación complementaria para (A) y u′ = f /y₁. Ahora supongamos que
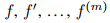
y

son funciones continuas en (a, b), donde m es un número entero positivo, y definen

Muestre que