| 9. Ecuaciones diferenciales | 9.12. Soluciones de Fourier de ecuaciones diferenciales parciales | Ejercicios propuestos para el Capítulo 9.12.4 |
9.12.4 Ecuación de Laplace en coordenadas polares
En la Sección 9.12.3 resolvimos problemas de valores en la frontera para la ecuación de Laplace sobre un rectángulo con lados paralelos a los ejes x, y. Ahora consideraremos los problemas de valores de frontera para la ecuación de Laplace sobre regiones con fronteras mejor descritas en términos de coordenadas polares. En este caso es apropiado considerar a u como función de (r, θ) y escribir la ecuación de Laplace en forma polar como
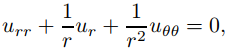 (9.12.4.1)
(9.12.4.1)
donde

y 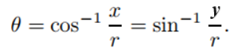
Comenzamos con el caso donde la región es un disco circular de radio ρ, con centro en el origen; es decir, queremos definir una solución formal del problema de valor en la frontera
 (9.12.4.2)
(9.12.4.2)
(Figura 9.12.4.1). Tenga en cuenta que (9.12.4.2) no impone ninguna restricción sobre u(r, θ) cuando r = 0. Abordaremos esta pregunta en el momento apropiado.

Figura 9.12.4.1 El problema del valor en la frontera (9.12.4.2)
Primero buscamos productos v(r, θ) = R(r)Θ(θ) que satisfagan (9.12.4.1). Para esta función,
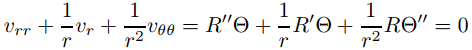
para todo (r, θ) con r ≠ 0 si

donde λ es una constante de separación. (Verifique). Esta ecuación es equivalente a
Θ′′ + λΘ = 0
y
r2R′′ + rR′ − λR = 0. (9.12.4.3)
Dado que (r, π) y (r, −π) son las coordenadas polares del mismo punto, imponemos condiciones de frontera periódicas en Θ; es decir,
Θ′′ + λΘ = 0, Θ(−π) = Θ(π), Θ′(−π) = Θ′(π). (9.12.4.4)
Como no queremos que RΘ sea idénticamente cero, λ debe ser un valor propio de (9.12.4.4) y Θ debe ser una función propia asociada. Del Teorema 9.11.1.6, los valores propios de (9.12.4.4) son λ0 = 0 con funciones propias asociadas Θ0 = 1 y, para n = 1, 2, 3, . . ., λn = n2, con función propia asociada cosnθ y sennθ por lo tanto,
Θn = αn cosnθ + βn sennθ
donde αn y βn son constantes.
Sustituyendo λ = 0 en (9.12.4.3) se obtiene
r2R′′ + rR′ = 0,
así

R0 = c2 + c1 en r. (9.12.4.5)
Si c1 ≠ 0 entonces
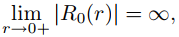
lo cual no tiene sentido si interpretamos u0(r, θ) = R0(r)Θ0(θ) = R0(r) como la distribución de temperatura en estado estacionario en un disco cuyo límite se mantiene a la temperatura constante R0(ρ). Por lo tanto, ahora requerimos que R0 esté acotado como r → 0+. Esto implica que c1 = 0, y tomamos c2 = 1. Por lo tanto, R0 = 1 y v0(r, θ) = R0(I)Θ0(θ) = 1. Nótese que v0 satisface (9.12.4.2) con f (θ) = 1.
Sustituyendo λ = n2 en (9.12.4.3) se obtiene la ecuación de Euler
 (9.12.4.6)
(9.12.4.6)
para Rn. El polinomio característico de esta ecuación es
s(s − 1) + s − n2 = (s − n)(s + n)
por lo que la solución general de (9.12.4.6) es
Rn = c1rn + c2r−n, (9.12.4.7)
por el Teorema 9.7.4.1. De acuerdo con nuestra suposición anterior sobre R0, ahora requerimos que Rn esté acotado cuando r → 0+. Esto implica que c2 = 0, y elegimos c1 = ρ−n. Entonces Rn(r) = rn/ρn, así

Ahora vn satisface (9.12.4.2) con
f (θ) = αn cosnθ + βn sennθ.
Más generalmente, si α0, α1,. . . , αm y β1, β2, . . . , βm son constantes arbitrarias entonces

satisface (9.12.4.2) con
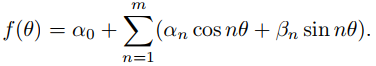
Esto motiva la siguiente definición.
Definición 9.12.4.1
La solución formal acotada del problema de valores en la frontera (9.12.4.2) es
 , (9.12.4.8)
, (9.12.4.8)
donde

es la serie de Fourier de f en [−π, π]; es decir,
 y
y  y
y 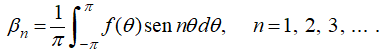
Ya que  converge para cada k si 0 < r < ρ, el Teorema 9.12.1.1 se puede usar para mostrar que si 0 < r < ρ entonces (9.12.4.8) se puede diferenciar término por término cualquier número de veces con respecto a r y θ. Dado que los términos en (9.12.4.8) satisfacen la ecuación de Laplace si r > 0, (9.12.4.8) satisface la ecuación de Laplace si 0 < r < ρ. Por lo tanto, dado que u(ρ, θ) = F(θ), u es una solución real de (9.12.4.2) si y solo si
converge para cada k si 0 < r < ρ, el Teorema 9.12.1.1 se puede usar para mostrar que si 0 < r < ρ entonces (9.12.4.8) se puede diferenciar término por término cualquier número de veces con respecto a r y θ. Dado que los términos en (9.12.4.8) satisfacen la ecuación de Laplace si r > 0, (9.12.4.8) satisface la ecuación de Laplace si 0 < r < ρ. Por lo tanto, dado que u(ρ, θ) = F(θ), u es una solución real de (9.12.4.2) si y solo si
F(θ) = f (θ), −π ≤ θ < π.
Del Teorema 9.11.2.2, esto es cierto si f es continua y uniforme a trozos en [−π, π] y f (−π) = f (π).
Ejemplo ilustrativo 9.12.4.1
Encuentre la solución formal acotada de (9.12.4.2) con f (θ) = θ(π2 − θ2).
Solución:
Del Ejemplo 9.11.2.6,

así que
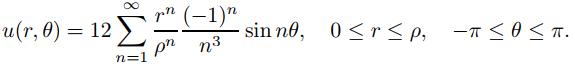 ♦
♦
Ejemplo ilustrativo 9.12.4.2
Defina la solución formal de
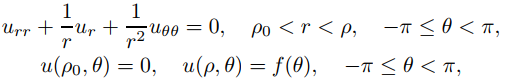 (9.12.4.9)
(9.12.4.9)
donde 0 < ρ0 < ρ (Figura 9.12.4.2).

Figura 9.12.4.2 El problema del valor en la frontera (9.12.4.9)
Solución:
Usamos la separación de variables exactamente como antes, excepto que ahora elegimos las constantes en (9.12.4.5) y (9.12.4.7) para que Rn(ρ0) = 0 para n = 0, 1, 2,. . . . En vista de la condición de Dirichlet no homogénea en el límite r = ρ, también es conveniente exigir que Rn(ρ) = 1 para n = 0, 1, 2,. . . . Te dejamos a ti verificar que
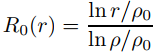 y
y 
satisface estos requisitos. Por lo tanto
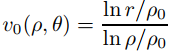
y

donde αn y βn son constantes arbitrarias.
Si α0, α1,. . . , αm y β1, β2, . . . , βm son constantes arbitrarias entonces
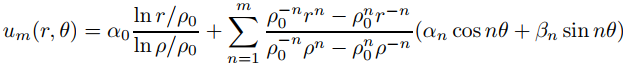
satisface (9.12.4.9), con

Esto nos motiva a definir la solución formal de (9.12.4.9) para f general como

donde
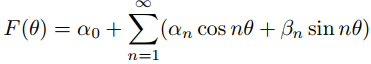
es la serie de Fourier de f en [−π, π].
Ejemplo ilustrativo 9.12.4.3
Defina la solución formal acotada de
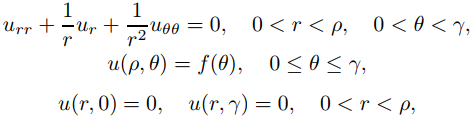 (9.12.4.10)
(9.12.4.10)
donde 0 < γ < 2π (Figura 9.12.4.3).

Figura 9.12.4.3 El problema de valor en la frontera (9.12.4.10)
Solución:
Ahora v(r, θ) = R(r)Θ(θ), donde
r2R′′ + rR′ − λR = 0 (9.12.4.11)
y
Θ′′ + λΘ = 0, Θ(0) = 0, Θ(γ) = 0. (9.12.4.12)
Del Teorema 9.11.1.2, los valores propios de (9.12.4.12) son λn = n2π2/γ2, con la función propia asociada Θn = sennπθ/γ, n = 1, 2, 3,. . . . Sustituyendo λ = n2π2/γ2 en (9.12.4.11) se obtiene la ecuación de Euler

El polinomio característico de esta ecuación es

así

por el Teorema 9.7.4.1. Para obtener una solución que permanezca acotada cuando r → 0+ hacemos c2 = 0. Debido a la condición de Dirichlet en r = ρ, es conveniente tener r(ρ) = 1; por lo tanto, tomamos c1 = ρ−nπ/γ, entonces

Ahora
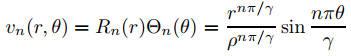
satisface (9.12.4.10) con

Más generalmente, si α1, α2, . . . , αm y son constantes arbitrarias entonces
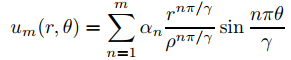
satisface (9.12.4.10) con
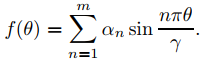
Esto nos motiva a definir la solución formal acotada de (9.12.4.10) como

donde
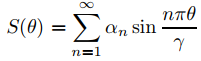
es la expansión del seno de Fourier de f en [0, γ]; es decir,

