| 9. Ecuaciones diferenciales | 9.8. La transformada de Laplace | Ejercicios propuestos para el Capítulo 9.8.7 |
9.8.7 ECUACIONES DE COEFICIENTES CONSTANTES CON IMPULSOS
Hasta ahora en este capítulo, hemos considerado problemas de valor inicial para la ecuación de coeficientes constantes
ay′′ + by′ + cy = f(t),
donde f es continua o continua por tramos en [0, ∞). En esta sección consideramos problemas de valor inicial donde f representa una fuerza que es muy grande por un corto tiempo y cero en caso contrario. Decimos que tales fuerzas son impulsivas. Las fuerzas impulsivas ocurren, por ejemplo, cuando dos objetos chocan. Dado que no es factible representar tales fuerzas como funciones continuas o continuas por partes, debemos construir un modelo matemático diferente para tratar con ellas.
Si f es una función integrable y f(t) = 0 para t fuera del intervalo [t0, t0 + h], entonces  se llama el impulso total de f. Estamos interesados en la situación idealizada donde h es tan pequeño que se puede suponer que el impulso total se aplica instantáneamente en t = t0. Decimos en este caso que f es una función impulso. En particular, denotamos por δ(t − t0) la función impulso con impulso total igual a uno, aplicado en t = t0. (La función de impulso δ(t) obtenida al establecer t0 = 0 es la función δ de Dirac.) Sin embargo, debe entenderse que δ(t − t0) no es una función en el sentido estándar, ya que nuestra “definición” implica que δ(t − t0) = 0 si t ≠ t0, mientras que
se llama el impulso total de f. Estamos interesados en la situación idealizada donde h es tan pequeño que se puede suponer que el impulso total se aplica instantáneamente en t = t0. Decimos en este caso que f es una función impulso. En particular, denotamos por δ(t − t0) la función impulso con impulso total igual a uno, aplicado en t = t0. (La función de impulso δ(t) obtenida al establecer t0 = 0 es la función δ de Dirac.) Sin embargo, debe entenderse que δ(t − t0) no es una función en el sentido estándar, ya que nuestra “definición” implica que δ(t − t0) = 0 si t ≠ t0, mientras que
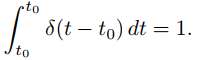
Del cálculo sabemos que ninguna función puede tener estas propiedades; sin embargo, existe una rama de las matemáticas conocida como teoría de las distribuciones donde la definición puede hacerse rigurosa. Dado que la teoría de las distribuciones está más allá del alcance de este libro, adoptaremos un enfoque intuitivo para las funciones de impulso.
Nuestra primera tarea es definir lo que queremos decir con la solución del problema de valor inicial
ay′′ + by′ + cy = δ(t − t0), y(0) = 0, y′(0) = 0,
donde t0 es un número fijo no negativo. El siguiente teorema motivará nuestra definición.
Teorema 9.8.7.1
Supongamos que t0 ≥ 0. Para cada número positivo h, sea yh la solución del problema de valor inicial
ayh′′ + byh′ + cyh = fh(t), yh(0) = 0, yh′ (0) = 0, (9.8.7.1)
donde
 (9.8.7.2)
(9.8.7.2)
entonces fh tiene un impulso total unitario igual al área del rectángulo sombreado en la Figura 9.8.7.1. Entonces
 (9.8.7.3)
(9.8.7.3)
donde
 ♦
♦
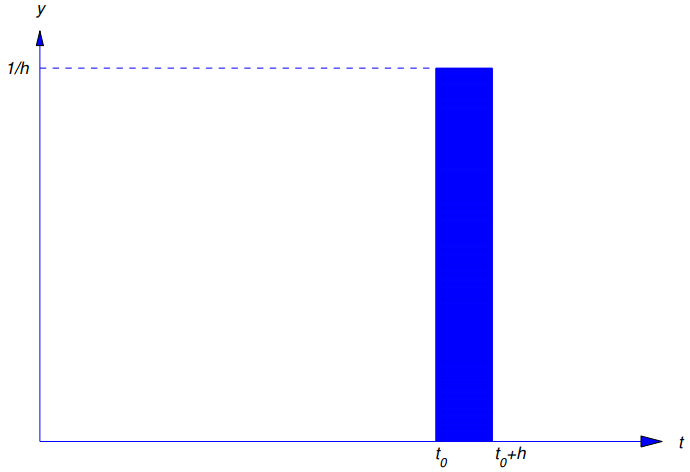
Figura 9.8.7.1 y = fh(t)
Prueba:
Tomando la transformada de Laplace en (9.8.7.1) se obtiene
(as2 + bs + c)Yh(s) = Fh(s),
así que
El teorema de convolución implica que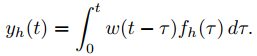
Por tanto, (9.8.7.2) implica que
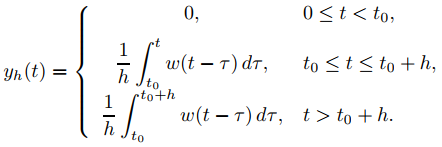 (9.8.7.4)
(9.8.7.4)
Como yh(t) = 0 para todo h si 0 ≤ t ≤ t0, se sigue que
lím h→0+ yh(t) = 0 si 0 ≤ t ≤ t0. (9.8.7.5)
Ahora mostraremos que
lím h→0+ yh(t) = 0 si w(t − t0) si t > t0. (9.8.7.6)
Suponga que t es fijo y t > t0. De (9.8.7.4),
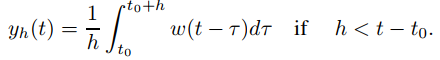 (9.8.7.7)
(9.8.7.7)
Ya que
 (9.8.7.8)
(9.8.7.8)
podemos escribir
De lo anterior y (9.8.7.7)
Por lo tanto
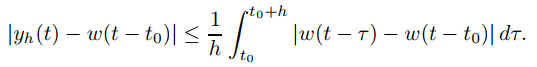 (9.8.7.9)
(9.8.7.9)
Ahora sea Mh el valor máximo de |w(t − τ) − w(t − t0)| ya que τ varía en el intervalo [t0, t0 + h].
(Recuerde que t y t0 son fijos). Entonces (9.8.7.8) y (9.8.7.9) implican que
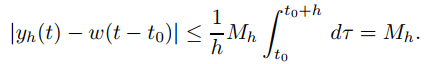 (9.8.7.10)
(9.8.7.10)
Pero limh→0+ Mh = 0, ya que w es continua. Por lo tanto (9.8.7.10) implica (9.8.7.6). Esto y (9.8.7.5) implican (9.8.7.3). ♦
El teorema 9.8.7.1 motiva la siguiente definición.
Definición 9.8.7.1
Si t0 > 0, entonces la solución del problema de valor inicial
ay′′ + by′ + cy = δ(t − t0), y(0) = 0, y′(0) = 0, (9.8.7.11)
se define como
y = u(t − t0)w(t − t0),
donde
 ♦
♦
En aplicaciones físicas donde la entrada f y la salida y de un dispositivo están relacionadas por la ecuación diferencial
ay′′ + by′ + cy = f(t),
w se llama la respuesta de impulso del dispositivo. Tenga en cuenta que w es la solución del problema de valor inicial
aw′′ + bw′ + cw = 0, w(0) = 0, w′(0) = 1/a, (9.8.7.12)
como se puede ver usando la transformada de Laplace para resolver este problema. (Verifique). Por otro lado, podemos resolver (9.8.7.12) por los métodos de la Sección 9.5.2 y mostrar que w está definido en (−∞, ∞) por
dependiendo de si el polinomio p(r) = ar2 + br + c tiene ceros reales distintos r1 y r2, un cero repetido r1 o ceros complejos conjugados λ ± iω. (En la mayoría de las aplicaciones físicas, los ceros del polinomio característico tienen partes reales negativas, por lo que limt→∞ w(t) = 0.) Esto significa que y = u(t − t0)w(t − t0) se define en ( −∞, ∞) y tiene las siguientes propiedades:
y(t) = 0, t < t0,
ay′′ + by′ + cy = 0 en (−∞, t0) y ( t0, ∞),
y′−(t0) = 0, y′+(t0) = 1/a (9.8.7.14)
(recuerde que y′−(t0) y y′+(t0) son derivadas por la derecha y por la izquierda, respectivamente) y y′(t0) no existe. Así, aunque definimos y = u(t − t0)w(t − t0) como la solución de (9.8.7.11), esta función no satisface la ecuación diferencial en (9.8.7.11) en t0, ya que no es diferenciable allí; de hecho (9.8.7.14) indica que un impulso provoca una discontinuidad de salto en la velocidad. (Para ver que esto es razonable, piensa en lo que sucede cuando golpeas una pelota con un bate). Esto significa que el problema de valor inicial (9.8.7.11) no tiene sentido si t0 = 0, ya que y′(0) no tiene sentido. No existe en este caso. Sin embargo y = u(t)w(t) se puede definir como la solución del problema de valor inicial modificado
ay′′ + by′ + cy = δ(t), y(0) = 0, y′−(0) = 0,
donde la condición sobre la derivada en t = 0 ha sido reemplazada por una condición sobre la derivada por la izquierda.
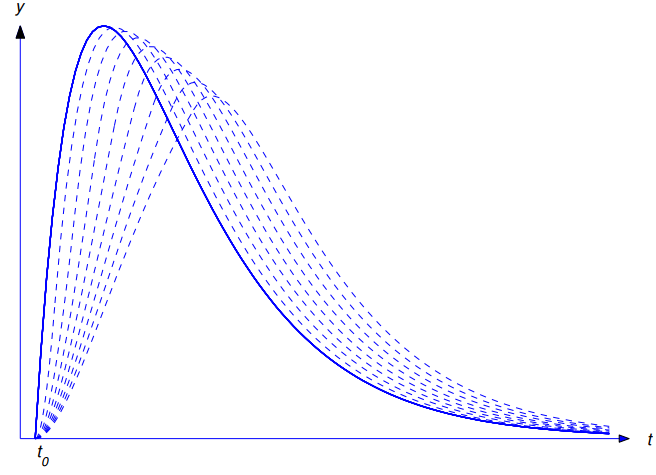
La Figura 9.8.7.2 ilustra el Teorema 9.8.7.1 para el caso en que la respuesta al impulso w es la primera expresión en (9.8.7.13) y r1 y r2 son distintos y ambos negativos. La curva continua en la figura es la gráfica de w. Las curvas punteadas son soluciones de (9.8.7.1) para varios valores de h. A medida que h disminuye, la gráfica de yh se mueve hacia la izquierda hacia la gráfica de w.
Ejemplo 9.8.7.1
Encuentre la solución del problema de valor inicial
ay′′ − 2y′ + y = δ(t − t0), y(0) = 0, y′(0) = 0 (9.8.7.15)
donde t0 > 0. Luego interprete la solución para el caso donde t0 = 0.
Solución:
Aquí
por lo que la Definición 9.8.7.2 da como resultado
como la solución de (9.8.7.15) si t0 > 0. Si t0 = 0, entonces (9.8.7.15) no tiene solución; sin embargo, y = u(t)te−t (que normalmente escribiríamos simplemente como y = te−t es la solución del problema de valor inicial modificado
ay′′ − 2y′ + y = δ(t), y(0) = 0, y′−(0) = 0,
La gráfica de y = u(t − t0)(t − t0)e−(t − t0) se muestra en la Figura 9.8.7.3. ♦
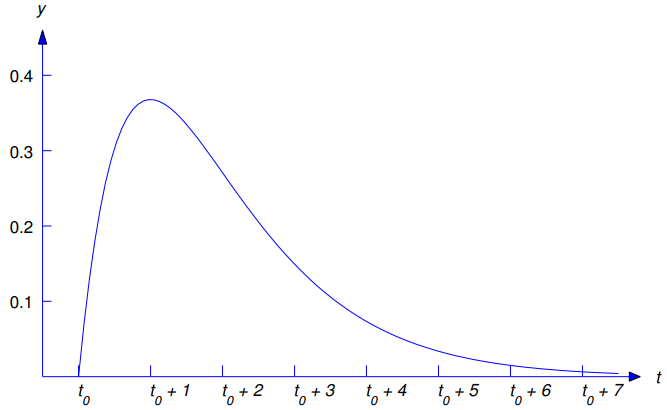
Figura 9.8.7.3 y = u(t − t0)(t − t0)e−(t − t0)
La Definición 9.8.7.1 y el principio de superposición motivan la siguiente definición.
Definición 9.8.7.2
Supongamos que α es una constante distinta de cero y f es continua por tramos en [0, ∞). Si t0 > 0, entonces la solución del problema de valor inicial
ay′′ + by′ + cy = f(t) + αδ(t − t0), y(0) = k0, y′(0) = k1
se define como
donde  es la solución de
es la solución de
ay′′ + by′ + cy = f(t), y(0) = k0, y′(0) = k1
Esta definición también se aplica si t0 = 0, siempre que la condición inicial y′(0) = k1 se reemplace por y′−(0) = k1. ♦
Ejemplo 9.8.7.2
Resolver el problema de valor inicial
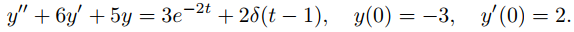 (9.8.7.16)
(9.8.7.16)
Solución:
Te dejamos a ti demostrar que la solución de
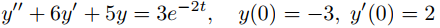
es
Ya que
la solución de (9.8.7.16) es
 (9.8.7.17) ♦
(9.8.7.17) ♦
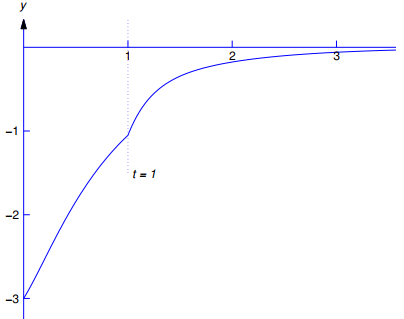
Figura 9.8.7.4 Gráfica de (9.8.7.17)
La Definición 9.8.7.2 puede ampliarse de manera obvia para cubrir el caso en el que la función forzada contiene más de un impulso.
Ejemplo 9.8.7.3
Resolver el problema de valor inicial
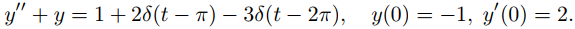 (9.8.7.18)
(9.8.7.18)
Solución:
Te dejamos a ti demostrar que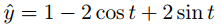
es la solución de
Ya que
la solución de (9.8.7.18) es
o
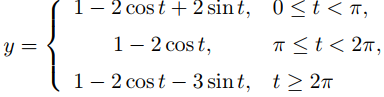 (9.8.7.19)
(9.8.7.19)

Figura 9.8.7.5 Gráfica de (9.8.7.19)
♦

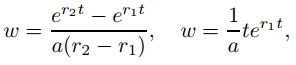 o
o 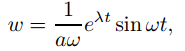 (
(