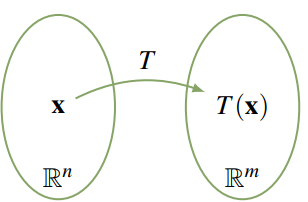
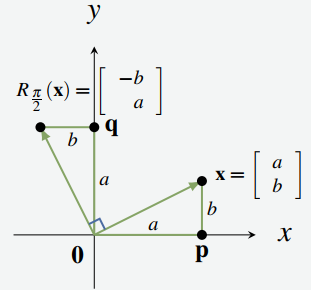
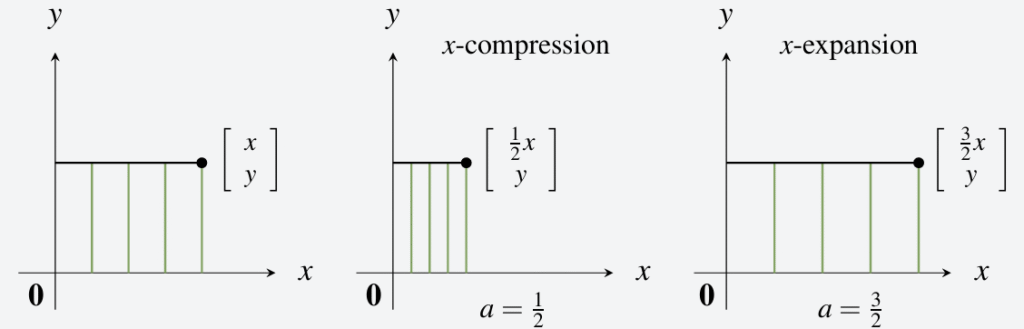
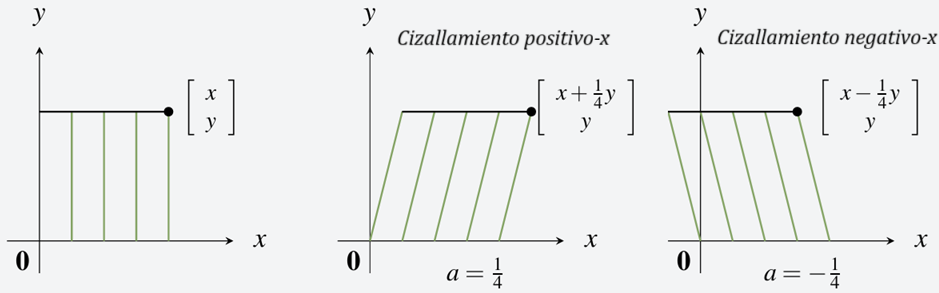
Álgebra lineal con aplicaciones
| 2. Álgebra de matrices | Ejercicios propuestos para el Capítulo 2.2 |
2.2. Multiplicación Matriz-Vector
Hasta ahora hemos utilizado matrices para resolver sistemas de ecuaciones lineales manipulando las filas de la matriz aumentada. En esta sección presentamos una forma diferente de describir sistemas lineales que hace más uso de la matriz de coeficientes del sistema y conduce a una forma útil de “multiplicar” matrices.
Vectores
Es un hecho bien conocido en geometría analítica que dos puntos en el plano con coordenadas (a1, a2) y (b1, b2) son iguales si y solo si a1 = b1 y a2 = b2. Además, una condición similar se aplica a los puntos (a1, a2, a3) en el espacio. Extendemos esta idea de la siguiente manera.
Una secuencia ordenada (a1, a2, …, an) de números reales se llama n-tupla ordenada. La palabra “ordenada” aquí refleja nuestra insistencia en que dos n-tuplas ordenadas son iguales si y solo si las entradas correspondientes son las mismas. En otras palabras
(a1, a2, …, an) = (b1, b2, …, bn) si y solo si a1 = b1, a2 = b2, …, y an = bn.
Por lo tanto, las 2-tuplas y las 3-tuplas ordenadas son solo los pares y triples ordenados familiares de la geometría.
Definición 2.4 El conjunto Rn de n-tuplas ordenadas
Sea R el conjunto de todos los números reales. El conjunto de todas las n-tuplas ordenadas de R tiene una notación especial:
Rn denota el conjunto de todas las n-tuplas ordenadas de números reales. ♦ números reales
Hay dos formas de uso común para denotar las n-tuplas en Rn: Como filas (r1, r2, …, rn) o como columnas  ; la notación que usamos depende del contexto. En cualquier caso, se denominan vectores o n-vectores y se denotarán en negrita, como x o v. Por ejemplo, una matriz A de m × n se escribirá como una fila de n columnas:
; la notación que usamos depende del contexto. En cualquier caso, se denominan vectores o n-vectores y se denotarán en negrita, como x o v. Por ejemplo, una matriz A de m × n se escribirá como una fila de n columnas:
A = [a1 a2 ··· an] donde aj denota la columna j de A para cada j.
Si x e y son dos n-vectores en Rn, está claro que la suma de su matriz x + y también está en Rn, al igual que el múltiplo escalar k x para cualquier número real k. Expresamos esta observación diciendo que Rn se cierra bajo la suma y la multiplicación escalar. En particular, todas las propiedades básicas del Teorema 2.1.1 son verdaderas para estos n-vectores. Estas propiedades son fundamentales y se utilizarán con frecuencia a continuación sin comentarios. En cuanto a las matrices en general, la matriz cero n × 1 se llama n-vector cero en Rn y, si x es un n-vector, el n-vector −x se llama x negativo.
Por supuesto, ya hemos encontrado estos n-vectores en la Sección 1.3 como soluciones a sistemas de ecuaciones lineales con n variables. En particular, definimos la noción de combinación lineal de vectores y mostramos que una combinación lineal de soluciones para un sistema homogéneo es nuevamente una solución. Claramente, una combinación lineal de n-vectores en Rn está nuevamente en Rn, un hecho que usaremos.
Multiplicación de matriz-vector
Dado un sistema de ecuaciones lineales, los lados izquierdos de las ecuaciones dependen solo de la matriz de coeficientes A y la columna x de las variables, y no de las constantes. Esta observación conduce a una idea fundamental en álgebra lineal: vemos los lados izquierdos de las ecuaciones como el “producto” Ax de la matriz A y el vector x. Este simple cambio de perspectiva conduce a una forma completamente nueva de ver los sistemas lineales, una que es muy útil y que ocupará nuestra atención a lo largo de este libro.
Para motivar la definición del “producto” Ax, considere primero el siguiente sistema de dos ecuaciones en tres variables:
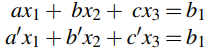 (2.2)
(2.2)
y deje que  denoten la matriz de coeficientes, la matriz de variables y la matriz de constantes, respectivamente. El sistema (2.2) se puede expresar como una única ecuación vectorial
denoten la matriz de coeficientes, la matriz de variables y la matriz de constantes, respectivamente. El sistema (2.2) se puede expresar como una única ecuación vectorial
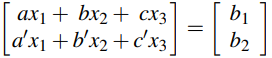
que a su vez se puede escribir de la siguiente manera:

Ahora observe que los vectores que aparecen en el lado izquierdo son solo las columnas

de la matriz de coeficientes A. Por tanto, el sistema (2.2) toma la forma
 (2.3)
(2.3)
Esto muestra que el sistema (2.2) tiene una solución si y solo si la matriz de constantes b es una combinación lineal de las columnas de A, y que en este caso las entradas de la solución son los coeficientes x1, x2 y x3 en esta combinación lineal.
Nota: Las combinaciones lineales se introdujeron en la Sección 1.3 para describir las soluciones de sistemas homogéneos de ecuaciones lineales. Se utilizarán ampliamente a continuación.
Además, esto es válido en términos generales. Si A es cualquier matriz de tamaño m × n, a menudo es conveniente ver a A como una fila de columnas. Es decir, si a1, a2, …, an son las columnas de A, escribimos 
y decir que 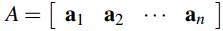 se da en términos de sus columnas.
se da en términos de sus columnas.
Ahora considere cualquier sistema de ecuaciones lineales con matriz de coeficientes A m × n. Si b es la matriz de constantes del sistema, y si  es la matriz de variables, entonces, exactamente como arriba, el sistema se puede escribir como una sola ecuación vectorial
es la matriz de variables, entonces, exactamente como arriba, el sistema se puede escribir como una sola ecuación vectorial
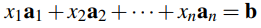 (2.4)
(2.4)
Ejemplo ilustrativo 2.2.1
Escriba el sistema  en la forma dada en (2.4).
en la forma dada en (2.4).
Solución:
 ◊
◊
Como se mencionó anteriormente, vemos el lado izquierdo de (2.4) como el producto de la matriz A y el vector x. Esta idea básica se formaliza en la siguiente definición:
Definición 2.5 Multiplicación matriz-vector
Sea  una matriz de tamaño m × n, escrita en términos de sus columnas a1, a2, …, an. Si
una matriz de tamaño m × n, escrita en términos de sus columnas a1, a2, …, an. Si 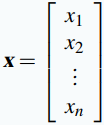 es cualquier n-vector, el producto Ax se define como el m-vector dado por:
es cualquier n-vector, el producto Ax se define como el m-vector dado por:
 ♦
♦
En otras palabras, si A es un matriz de tamaño m × n y x es un n-vector, el producto Ax es la combinación lineal de las columnas de A donde los coeficientes son las entradas de x (en orden).
Tenga en cuenta que si A es una matriz m × n, el producto Ax solo se define si x es un n-vector y entonces el vector Ax es un m-vector porque esto es cierto para cada columna aj de A. Pero en este caso el sistema de ecuaciones lineales con matriz de coeficientes A y vector de constantes b toma la forma de una sola ecuación matricial
Ax = b
El siguiente teorema combina la Definición 2.5 y la Ecuación (2.4) y resume la discusión anterior.
Recuerde que se dice que un sistema de ecuaciones lineales es consistente si tiene al menos una solución.
Teorema 2.2.1
1. Todo sistema de ecuaciones lineales tiene la forma Ax = b donde A es la matriz de coeficientes, b es la matriz de constantes y x es la matriz de variables.
2. El sistema Ax = b es consistente si y solo si b es una combinación lineal de las columnas de A.
3. Si a1, a2, …, an son las columnas de A y si  , entonces x es una solución del sistema lineal Ax = b si y solo si x1, x2, …, xn son una solución de la ecuación vectorial
, entonces x es una solución del sistema lineal Ax = b si y solo si x1, x2, …, xn son una solución de la ecuación vectorial
 ◊
◊
Un sistema de ecuaciones lineales en la forma Ax = b como en (1) del Teorema 2.2.1 se dice que está escrito en forma matricial. Esta es una forma útil de ver los sistemas lineales como constataremos más adelante.
El Teorema 2.2.1 transforma el problema de resolver el sistema lineal Ax = b en el problema de expresar la matriz de constantes b como una combinación lineal de las columnas de la matriz de coeficientes A. Dicho cambio de perspectiva es muy útil porque un enfoque o el otro pueden ser mejores en una situación particular; la importancia del teorema es que hay una opción.
Ejemplo ilustrativo 2.2.2
Si 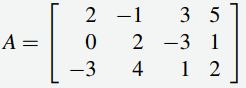 y
y  , calcule Ax.
, calcule Ax.
Solución:
De acuerdo con la Definición 2.5:
 ◊
◊
Ejemplo ilustrativo 2.2.3
Dadas las columnas a1, a2, a3 y a4 en R4, escriba 2a1 −3a2 + 5a3 + a4 en la forma Ax donde A es una matriz y x es un vector.
Solución:
Aquí la columna de coeficientes es  . Por tanto, la Definición 2.5 da
. Por tanto, la Definición 2.5 da
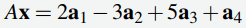
donde  es la matriz con a1, a2, a3 y a4 como sus columnas.
es la matriz con a1, a2, a3 y a4 como sus columnas.
Ejemplo ilustrativo 2.2.4
Suponga que  es una matriz de tamaño 3 × 4 dada en términos de sus columnas
es una matriz de tamaño 3 × 4 dada en términos de sus columnas
 En cada caso a continuación, exprese b como una combinación lineal de a1, a2, a3 y a4, o demuestre que no es una combinación lineal. Explica qué significa tu respuesta para el sistema correspondiente Ax = b de ecuaciones lineales.
En cada caso a continuación, exprese b como una combinación lineal de a1, a2, a3 y a4, o demuestre que no es una combinación lineal. Explica qué significa tu respuesta para el sistema correspondiente Ax = b de ecuaciones lineales.

Solución:
Según el Teorema 2.2.1, b es una combinación lineal de a1, a2, a3 y a4 si y solo si el sistema Ax = b es consistente (es decir, tiene una solución). Entonces, en cada caso, llevamos la matriz aumentada [A | b] del sistema Ax = b a forma reducida.
a. Aquí  , por lo que el sistema Ax = b no tiene solución en este caso. Por tanto, b no es una combinación lineal de a1, a2, a3 y a4.
, por lo que el sistema Ax = b no tiene solución en este caso. Por tanto, b no es una combinación lineal de a1, a2, a3 y a4.
b. Ahora  , entonces el sistema Ax = b es consistente. Por tanto, b es una combinación lineal de a1, a2, a3 y a4 en este caso. De hecho, la solución general es x1 = 1 − 2s − t, x2 = 2 + s − t, x3 = s, y x4 = t donde s y t son parámetros arbitrarios. Por eso
, entonces el sistema Ax = b es consistente. Por tanto, b es una combinación lineal de a1, a2, a3 y a4 en este caso. De hecho, la solución general es x1 = 1 − 2s − t, x2 = 2 + s − t, x3 = s, y x4 = t donde s y t son parámetros arbitrarios. Por eso  para cualquier elección de s y t. Si tomamos s = 0 y t = 0, esto se convierte en a1 + 2a2 = b, mientras que tomando s = 1 = t da −2a1 + 2a2 + a3 + a4 = b.
para cualquier elección de s y t. Si tomamos s = 0 y t = 0, esto se convierte en a1 + 2a2 = b, mientras que tomando s = 1 = t da −2a1 + 2a2 + a3 + a4 = b.
Ejemplo ilustrativo 2.2.5
Tomando A como la matriz cero, tenemos 0x = 0 para todos los vectores x según la Definición 2.5 porque cada columna de la matriz cero es cero. De manera similar, A0 = 0 para todas las matrices A porque cada entrada del vector cero es cero.
Ejemplo ilustrativo 2.2.6
Si  , demuestre que Ix = x para cualquier vector x en R3.
, demuestre que Ix = x para cualquier vector x en R3.
Solución:
Si  , entonces la Definición 2.5 da
, entonces la Definición 2.5 da

La matriz I del Ejemplo 2.2.6 se denomina matriz identidad de 3 × 3 y volveremos a encontrar tales matrices en el Ejemplo 2.2.11 a continuación. Antes de continuar, desarrollamos algunas propiedades algebraicas de la multiplicación matriz-vector que se utilizan ampliamente en todo el álgebra lineal.
Teorema 2.2.2
Sean A y B matrices de m×n, y sean x e y vectores de n dimensiones en Rn. Entonces:
1. A(x + y) = Ax + Ay.
2. A(ax) = a(Ax) = (aA)x para todos los escalares a.
3. (A + B)x = Ax + Bx.
♦
Demostración
Vamos a demostrar (3); las otras verificaciones son similares y se dejan como ejercicios. Sea A = [a1 a2 ⋯ an] y B = [b1 b2 ⋯ bn] dados en términos de sus columnas. Dado que sumar dos matrices es lo mismo que sumar sus columnas, tenemos:
A + B = [a1 + b1 a2 + b2 ··· an + bn]
Si nosotros escribimos 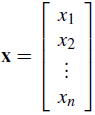 la Definición 2.5 da
la Definición 2.5 da
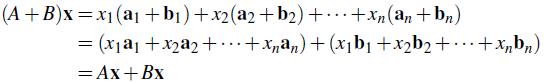 ♦
♦
El Teorema 2.2.2 permite realizar cálculos de matriz-vector de forma muy parecida a la aritmética ordinaria. Por ejemplo, para cualesquiera matrices A y B de tamaño m × n y cualesquiera n-vectores x e y, tenemos:
A(2x − 5y) = 2Ax − 5Ay y (3A − 7B)x = 3Ax − 7Bx
Usaremos tales manipulaciones a lo largo del libro, a menudo sin mencionarlas.
Ecuaciones lineales
El Teorema 2.2.2 también proporciona una forma útil de describir las soluciones de un sistema
Ax = b
de ecuaciones lineales. Hay un sistema relacionado
Ax = 0
llamado sistema homogéneo asociado, obtenido del sistema original Ax = b reemplazando todas las constantes por ceros. Supongamos que x1 es una solución de Ax = b y x0 es una solución de Ax = 0 (es decir, Ax1 = b y Ax0 = 0). Entonces x1 + x0 es otra solución de Ax = b. De hecho, el Teorema 2.2.2 da
A(x1 + x0) = Ax1 + Ax0 = b + 0 = b
Esta observación tiene una útil contraparte.
Teorema 2.2.3
Supongamos que x1 es cualquier solución particular del sistema Ax = b de ecuaciones lineales. Entonces toda solución x2 de Ax = b tiene la forma
x2 = x0 + x1
para alguna solución x0 del sistema homogéneo asociado Ax = 0. ♦
Prueba
Supongamos que x2 también es una solución de Ax = b, de modo que Ax2 = b. Escribe x0 = x2 − x1. Entonces x2 = x0 + x1 y, usando el Teorema 2.2.2, calculamos
Ax0 = A(x2 − x1) = Ax2 − Ax1 = b − b = 0
Por tanto, x0 es una solución del sistema homogéneo asociado Ax = 0. ♦
Tenga en cuenta que la eliminación gaussiana proporciona una de esas representaciones.
Ejemplo ilustrativo 2.2.7
Exprese cada solución del siguiente sistema como la suma de una solución particular y una solución del sistema homogéneo asociado.
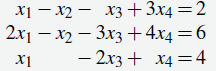
Solución:
La eliminación gaussiana da x1 = 4 + 2s − t, x2 = 2 + s + 2t, x3 = s y x4 = t donde s y t son parámetros arbitrarios. Por tanto, la solución general se puede escribir

De este modo 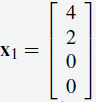 es una solución particular (donde s = 0 = t), y
es una solución particular (donde s = 0 = t), y 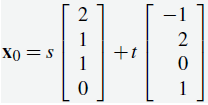 da todas las soluciones al sistema homogéneo asociado. (Para ver por qué esto es así, realice la eliminación gaussiana nuevamente pero con todas las constantes iguales a cero). ♦
da todas las soluciones al sistema homogéneo asociado. (Para ver por qué esto es así, realice la eliminación gaussiana nuevamente pero con todas las constantes iguales a cero). ♦
El siguiente resultado útil se incluye sin pruebas.
Teorema 2.2.4
Sea Ax = b un sistema de ecuaciones con matriz aumentada 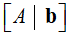 . Escriba rango A = r.
. Escriba rango A = r.
- rango
 es r o r + 1.
es r o r + 1. - El sistema es consistente si y sólo si el rango
 = r.
= r. - El sistema es inconsistente si y sólo si el rango
 = r + 1. ♦
= r + 1. ♦
El Producto Punto
La Definición 2.5 no es siempre la manera más sencilla de calcular un producto matriz-vector A x, porque requiere identificar explícitamente las columnas de A. Hay otra forma de encontrar dicho producto que utiliza la matriz A como un todo, sin referencia a sus columnas, y por lo tanto es útil en la práctica. El método depende de la siguiente noción.
Definición 2.6 Producto Punto en \(\mathbb{R}^n\)
Si \((a_1, a_2, \dots, a_n)\) y \((b_1, b_2, \dots, b_n)\) son dos $n$-tuplas ordenadas, su producto punto se define como el número
$$ a_1 b_1 + a_2 b_2 + \dots + a_n b_n $$obtenido al multiplicar las entradas correspondientes y sumar los resultados.
Para ver cómo esto se relaciona con los productos de matrices, sea $A$ una matriz de $3 \times 4$ y sea $\mathbf{x}$ un $4$-vector. Escribiendo
$$ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} \quad \text{y} \quad A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix} $$en la notación de la Sección 2.1, calculamos
$$ \mathbf{A}\mathbf{x} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = x_1 \begin{bmatrix} a_{11} \\ a_{21} \\ a_{31} \end{bmatrix} + x_2 \begin{bmatrix} a_{12} \\ a_{22} \\ a_{32} \end{bmatrix} + x_3 \begin{bmatrix} a_{13} \\ a_{23} \\ a_{33} \end{bmatrix} + x_4 \begin{bmatrix} a_{14} \\ a_{24} \\ a_{34} \end{bmatrix} $$ $$ = \begin{bmatrix} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + a_{14} x_4 \\ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + a_{24} x_4 \\ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + a_{34} x_4 \end{bmatrix} $$De esto vemos que cada entrada de $\mathbf{A}\mathbf{x}$ es el producto punto de la fila correspondiente de $A$ con $\mathbf{x}$. Este cálculo se mantiene en general, y registramos el resultado en el Teorema 2.2.5.
Teorema 2.2.5: Regla del Producto Punto
Sea \(A\) una matriz de \(m \times n\) y sea \(\mathbf{x}\) un \(n\)-vector. Entonces, cada entrada del vector \(\mathbf{A}\mathbf{x}\) es el producto punto de la fila correspondiente de \(A\) con \(\mathbf{x}\).
Este resultado se utiliza ampliamente en toda el álgebra lineal.
Si A es de tamaño m × n y x es un -vector, el cálculo de Ax mediante la regla del producto punto es más sencillo que usar la Definición 2.5, porque el cálculo puede realizarse directamente sin referencia explícita a las columnas de A (como en la Definición 2.5).
La primera componente de Ax es el producto punto de la fila 1 de A con x. En cálculos manuales esto se obtiene recorriendo horizontalmente la primera fila de A, recorriendo verticalmente la columna x, multiplicando las entradas correspondientes y sumando los resultados. Las demás componentes de Ax se calculan del mismo modo usando las otras filas de A con la columna x.
En general, calcule la entrada i de Ax de la siguiente manera (véase el diagrama):
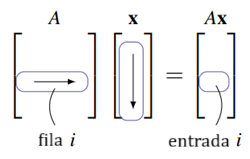
Recorra horizontalmente la fila i de A y verticalmente la columna x, multiplique las entradas correspondientes y sume los resultados.
Como ilustración, rehacemos el Ejemplo 2.2.2 usando la regla del producto punto en lugar de la Definición 2.5.
Ejemplo 2.2.8
Si \( A = \begin{bmatrix} 2 & -1 & 3 & 5 \\ 0 & 2 & -3 & 1 \\ -3 & 4 & 1 & 2 \end{bmatrix} \) y \( \mathbf{x} = \begin{bmatrix} 2 \\ 1 \\ 0 \\ -2 \end{bmatrix} \), calcule $A\mathbf{x}$.
Solución:
Las entradas de $A\mathbf{x}$ son los productos escalares de las filas de $A$ con $\mathbf{x}$:
$$ A\mathbf{x} = \begin{bmatrix} 2 & -1 & 3 & 5 \\ 0 & 2 & -3 & 1 \\ -3 & 4 & 1 & 2 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\ 0 \\ -2 \end{bmatrix} = \begin{bmatrix} 2 \cdot 2 + (-1)1 + 3 \cdot 0 + 5(-2) \\ 0 \cdot 2 + 2 \cdot 1 + (-3)0 + 1(-2) \\ (-3)2 + 4 \cdot 1 + 1 \cdot 0 + 2(-2) \end{bmatrix} = \begin{bmatrix} -7 \\ 0 \\ -6 \end{bmatrix} $$Por supuesto, esto concuerda con el resultado en el Ejemplo 2.2.2.
Ejemplo 2.2.9
Escriba el siguiente sistema de ecuaciones lineales en la forma $A\mathbf{x} = \mathbf{b}$.
$$ 5x_1 – x_2 + 2x_3 + x_4 – 3x_5 = 8 $$ $$ x_1 + x_2 + 3x_3 – 5x_4 + 2x_5 = -2 $$ $$ -x_1 + x_2 – 2x_3 – 3x_5 = 0 $$Solución:
Escribimos: $$ A = \begin{bmatrix} 5 & -1 & 2 & 1 & -3 \\ 1 & 1 & 3 & -5 & 2 \\ -1 & 1 & -2 & 0 & -3 \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} 8 \\ -2 \\ 0 \end{bmatrix}, \quad \text{y} \quad \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} $$
Entonces, la regla del producto escalar nos da $A\mathbf{x}$: $$ A\mathbf{x} = \begin{bmatrix} 5x_1 – x_2 + 2x_3 + x_4 – 3x_5 \\ x_1 + x_2 + 3x_3 – 5x_4 + 2x_5 \\ -x_1 + x_2 – 2x_3 – 3x_5 \end{bmatrix} $$
Por lo que las entradas de $A\mathbf{x}$ son los lados izquierdos de las ecuaciones en el sistema lineal. Por lo tanto, el sistema se convierte en $A\mathbf{x} = \mathbf{b}$ porque las matrices son iguales si y solo si sus entradas correspondientes son iguales.
Ejemplo 2.2.10
Si $A$ es la matriz nula $m \times n$, entonces $A\mathbf{x} = \mathbf{0}$ para cada vector $\mathbf{x}$ de $n$ componentes.
Solución:
Para cada $k$, la entrada $k$ de $A\mathbf{x}$ es el producto escalar de la fila $k$ de $A$ con $\mathbf{x}$, y esto es cero porque la fila $k$ de $A$ consta de ceros.
$$ \begin{bmatrix} 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix}_{m \times n} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}_{m \times 1} $$
Definición 2.7 La Matriz Identidad
Para cada $n \ge 2$, la matriz identidad $I_n$ es la matriz $n \times n$ con $1$s en la diagonal principal (superior izquierda a inferior derecha), y ceros en el resto.
Las primeras matrices identidad son:
\[ I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \qquad I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \qquad I_4 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}, \ \ldots \]En el Ejemplo 2.2.6 mostramos que I3x = x para todo 3-vector x usando la Definición 2.5. El siguiente resultado muestra que esto se cumple en general y es la razón del nombre.
Ejemplo 2.2.11
Para cada \(n \ge 2\) tenemos para cada \(n\)-vector en \(\mathbb{R}^n\).
Solución.
Verificamos el caso \(n = 4\). Dado el 4-vector , la regla del producto punto da:
En general, porque la entrada \(k\) de es el producto punto de la fila \(k\) de \(I_n\) con , y la fila \(k\) de \(I_n\) tiene \(1\) en la posición \(k\) y ceros en el resto.
Ejemplo 2.2.12
Sea cualquier matriz \(m \times n\) con columnas , , …, . Si denota la columna \(j\) de la matriz identidad , entonces:
Solución.
Escribimos donde , pero para todo \(i \ne j\).
Entonces, el Teorema 2.2.5 da:
El Ejemplo 2.2.12 será referido más adelante; por ahora lo usamos para demostrar:
Demostración. Escriba $A = \left[ \mathbf{a}_1 \ \mathbf{a}_2 \ \cdots \ \mathbf{a}_n \right]$ y $B = \left[ \mathbf{b}_1 \ \mathbf{b}_2 \ \cdots \ \mathbf{b}_n \right]$ en términos de sus columnas. Basta con mostrar que $\mathbf{a}_k = \mathbf{b}_k$ se cumple para todo $k$. Pero estamos asumiendo que $A\mathbf{e}_k = B\mathbf{e}_k$, lo cual da $\mathbf{a}_k = \mathbf{b}_k$ por el Ejemplo 2.2.12. $\square$
Hemos introducido la multiplicación matriz–vector como una nueva manera de pensar sobre los sistemas de ecuaciones lineales. Pero también tiene varios otros usos. Resulta que muchas operaciones geométricas pueden describirse mediante la multiplicación de matrices, y ahora investigaremos cómo sucede esto. Como beneficio adicional, esta descripción proporciona una “imagen” geométrica de una matriz al revelar el efecto sobre un vector cuando es multiplicado por A. Esta “visión geométrica” de las matrices es una herramienta fundamental para comprenderlas.
Transformaciones
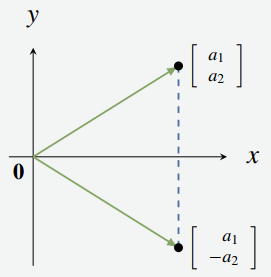
El conjunto \(\mathbb{R}^2\) tiene una interpretación geométrica como el plano euclidiano, donde un vector \[ \begin{bmatrix} a_1\\[4pt] a_2 \end{bmatrix} \in \mathbb{R}^2 \] representa el punto \((a_1, a_2)\) en el plano (véase la Figura 2.2.1). De este modo, consideramos \(\mathbb{R}^2\) como el conjunto de todos los puntos del plano.
En consecuencia, nos referiremos a los vectores en \(\mathbb{R}^2\) como puntos, y denotaremos sus coordenadas como una columna en lugar de una fila. Para reforzar esta interpretación geométrica del vector \[ \begin{bmatrix} a_1\\[4pt] a_2 \end{bmatrix} \], se representa gráficamente mediante una flecha desde el origen \[ \begin{bmatrix} 0\\[4pt] 0 \end{bmatrix} \] hasta el vector, como en la Figura 2.2.1.


De manera similar, identificamos \(\mathbb{R}^3\) con el espacio tridimensional escribiendo un punto \((a_1, a_2, a_3)\) como el vector \[ \begin{bmatrix} a_1\\[4pt] a_2\\[4pt] a_3 \end{bmatrix} \] en \(\mathbb{R}^3\), representado nuevamente por una flecha desde el origen hasta el punto, como en la Figura 2.2.2.
De esta manera, los términos “punto” y “vector” significan lo mismo en el plano o en el espacio.
Comenzamos describiendo una transformación geométrica particular del plano R2.
Ejemplo 2.2.13
Considere la transformación de dada por reflexión en el eje . Esta operación lleva el vector a su reflexión como en la Figura 2.2.3. Ahora observe que
por lo tanto, reflejar en el eje se puede lograr multiplicando por la matriz .
Como tal, es una generalización de las funciones familiares que llevan un número a otro número real .