| 9. Ecuaciones diferenciales | 9.4. Aplicaciones de ecuaciones de primer orden | Ejercicios propuestos para el Capítulo 9.4.4 |
9.4.4 Ecuaciones autónomas de segundo orden
Una ecuación diferencial de segundo orden que se puede escribir como
y′′ = F(y, y′) (9.4.4.1)
donde F es independiente de t, se dice que es autónoma. Una ecuación autónoma de segundo orden se puede convertir en una ecuación de primer orden que relaciona v = y′ y y. Si hacemos que v = y′, (9.4.4.1) se convierte en
v′ = F(y, v). (9.4.4.2)
(9.4.4.3)
(9.4.4.2) se puede reescribir como
(9.4.4.4)
Las curvas integrales de (9.4.4.4) se pueden trazar en el plano (y, v), que se denomina plano de fase de Poincaré de (9.4.4.1). Si y es una solución de (9.4.4.1), entonces y = y(t), v = y′(t) es una ecuación paramétrica para una curva integral de (9.4.4.4). Llamaremos a estas curvas integrales trayectorias de (9.4.4.1), y llamaremos a (9.4.4.4) el plano de fase equivalente de (9.4.4.1).
En esta sección consideraremos ecuaciones autónomas que se pueden escribir como
y′′ + q(y, y′)y′ + p(y) = 0. (9.4.4.5)
Las ecuaciones de esta forma a menudo surgen en aplicaciones de la segunda ley del movimiento de Newton. Por ejemplo, suponga que y es el desplazamiento de un objeto en movimiento con masa m. Es razonable pensar en dos tipos de fuerzas independientes del tiempo que actúan sobre el objeto. Un tipo, como la gravedad, depende solo de la posición. Podríamos escribir una fuerza como −mp(y). El segundo tipo, como la resistencia atmosférica o la fricción, puede depender de la posición y la velocidad. (Las fuerzas que dependen de la velocidad se denominan fuerzas de amortiguamiento). Escribimos esta fuerza como −mq(y, y′)y′, donde q(y, y′) suele ser una función positiva y hemos puesto el factor y′ afuera para hacer explícito que la fuerza está en la dirección opuesta al movimiento. En este caso, la segunda ley del movimiento de Newton conduce a (9.4.4.5).
El plano de fase equivalente de (9.4.4.5) es
(9.4.4.6)
Algunas declaraciones que haremos sobre las propiedades de (9.4.4.5) y (9.4.4.6) son intuitivamente razonables, pero difíciles de probar. Por lo tanto, nuestra presentación en esta sección será informal: simplemente diremos cosas sin demostración, todas las cuales son verdaderas si suponemos que p = p(y) es continuamente diferenciable para todo y y q = q(y, v) es continuamente diferenciable para todo (y, v). Comenzamos con las siguientes afirmaciones:
- Afirmación 1. Si y0 y v0 son números reales arbitrarios, entonces (9.4.4.5) tiene una solución única en (−∞, ∞) tal que y(0) = y0 y y′(0) = v0.
- Afirmación 2. Si y = y(t) es una solución de (9.4.4.5) y τ es cualquier constante, entonces y1 = y(t − τ) también es una solución de (9.4.4.5), y y e y1 tienen la misma trayectoria.
- Afirmación 3. Si dos soluciones y e y1 de (9.4.4.5) tienen la misma trayectoria, entonces y1(t) = y(t − τ) para alguna constante τ.
- Afirmación 4. Las trayectorias distintas de (9.4.4.5) no pueden intersecarse; es decir, si dos trayectorias de (9.4.4.5) se cortan, son idénticas.
- Afirmación 5. Si la trayectoria de una solución de (9.4.4.5) es una curva cerrada, entonces (y(t), v(t)) recorre la trayectoria en un tiempo finito T, y la solución es periódica con período T; es decir, y(t + T) = y(t) para todo t en (−∞, ∞).
Si 
es una constante tal que p() = 0 entonces y ≡ es una solución constante de (9.4.4.5). Decimos que es un equilibrio de (9.4.4.5) y (, 0) es un punto crítico de la ecuación equivalente del plano de fase (9.4.4.6). Decimos que el equilibrio y el punto crítico son estables si, para cualquier ε > 0, por pequeño que sea, existe un δ > 0, suficientemente pequeño, tal que si
entonces la solución del problema de valor inicial
y′′ + q(y, y′)y′ + p(y) = 0, y(0) = y0, y′(0) = v0
satisface la desigualdad
para todo t > 0. La Figura 9.4.4.1 ilustra la interpretación geométrica de esta definición en el plano de fase de Poincaré: si (y0, v0) está en el círculo sombreado más pequeño (con radio δ), entonces (y(t), v( t)) debe estar en el círculo más grande (con radio ε) para todo t > 0.
Figura 9.4.4.1 Estabilidad: si (y0, v0) está en el círculo más pequeño, entonces (y(t), v(t)) está en el círculo más grande para todo t > 0
Si un equilibrio y el punto crítico asociado no son estables, decimos que son inestables. Para ver si realmente entiende lo que significa estable, trate de dar una definición directa de inestable (Ejercicio 22). Ilustraremos ambas definiciones en los siguientes ejemplos.
El caso no amortiguado
Comenzaremos con el caso donde q ≡ 0, entonces y′′ + q(y, y′)y′ + p(y) = 0 (9.4.4.5) se reduce a
y′′ + p(y) = 0. (9.4.4.7)
Decimos que esta ecuación, así como cualquier situación física que pueda modelar, no está amortiguada. El equivalente en el plano de fase de (9.4.4.7) es la ecuación separable
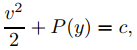(9.4.4.8)
donde c es una constante de integración y P(y) = ∫p(y)dy es una antiderivada de p.
Si (9.4.4.7) es la ecuación de movimiento de un objeto de masa m, entonces mv2/2 es la energía cinética y mP(y) es la energía potencial del objeto; así, (9.4.4.8) dice que la energía total del objeto permanece constante, o se conserva. En particular, si una trayectoria pasa por un punto dado (y0, v0) entonces
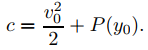
Ejemplo ilustrativo 9.4.4.1
[El resorte no amortiguado – Sistema de masas] Considere un objeto con masa m suspendido de un resorte y moviéndose verticalmente. Sea y el desplazamiento del objeto desde la posición que ocupa cuando está suspendido en reposo del resorte (Figura 9.4.4.2)
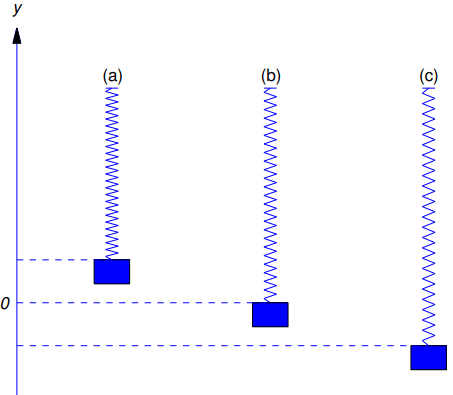
Figura 9.4.4.2 (a) y > 0 (b) y = 0 (c) < 0
Suponga que si la longitud del resorte cambia en una cantidad ∆L (positiva o negativa), entonces el resorte ejerce una fuerza opuesta con magnitud k|∆L|, donde k es una constante positiva. En la Sección 9.6.1 se demostrará que si la masa del resorte es despreciable en comparación con m y ninguna otra fuerza actúa sobre el objeto, entonces la segunda ley del movimiento de Newton implica que
my′′ = −ky, (9.4.4.9)
que se puede escribir en la forma (9.4.4.7) con p(y) = ky/m. Esta ecuación se puede resolver fácilmente mediante un método que estudiaremos en la Sección 9.5.2, pero ese método no está disponible aquí. En su lugar, consideraremos el plano de fase equivalente a (9.4.4.9).
De (9.4.4.3), podemos reescribir (9.4.4.9) como la ecuación separable
Integrando esto se obtiene
lo que implica que
mv2 + ky2 = ρ (9.4.4.10)
(ρ = 2c). Esto define una elipse en el plano de fase de Poincaré (Figura 9.4.4.3).
Figura 9.4.4.3 Trayectorias de my′′ + ky = 0
Podemos identificar ρ estableciendo t = 0 en (9.4.4.10); por tanto, ρ = mv02 + ky02, donde y0 = y(0) y v0 = v(0). Para determinar los valores máximo y mínimo de y establecemos v = 0 en (9.4.4.10); de este modo,
ymax = R y ymin = −R, con 
(9.4.4.11)
La ecuación (9.4.4.9) tiene exactamente un equilibrio, y = 0, y es estable. Puede ver intuitivamente por qué esto es así: si el objeto se desplaza en cualquier dirección desde el equilibrio, el resorte intenta traerlo de vuelta.
En este caso podemos encontrar y explícitamente como una función de t. (¡No espere que esto suceda en problemas más complicados!) Si v > 0 en un intervalo I, (9.4.4.10) implica que
en I. Esto es equivalente a
donde 
(9.4.4.12)
Desde
(observe (9.4.4.11)), (9.4.4.12) implica que hay una constante φ tal que
o
y = Rsen(ω0t + φ)
para todo t en I. Aunque obtuvimos esta función suponiendo que v > 0, puede verificar fácilmente que y satisface (9.4.4.9) para todos los valores de t. Así, el desplazamiento varía periódicamente entre −R y R, con periodo T = 2π/ω0 (Figura 9.4.4.4). (Si ha tomado un curso de mecánica elemental, puede reconocer esto como un movimiento armónico simple).
Figura 9.4.4.4 y = Rsen(ω0t + φ)
Ejemplo ilustrativo 9.4.4.2
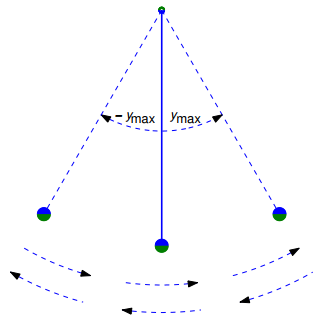
[El péndulo no amortiguado] Ahora consideramos el movimiento de un péndulo con masa m, unido al extremo de una barra ingrávida con longitud L que gira sobre un eje sin fricción (Figura 9.4.4.5). Suponemos que no hay resistencia del aire.
Sea y el ángulo medido desde la posición de reposo (verticalmente hacia abajo) del péndulo, como se muestra en la figura 9.4.4.5. La segunda ley del movimiento de Newton dice que el producto de m y la aceleración tangencial es igual a la componente tangencial de la fuerza gravitatoria; por lo tanto, de la Figura 9.4.4.5,
mLy′′ = −mgseny,
o
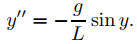(9.4.4.13)
Como sennπ = 0 si n es cualquier número entero, (9.4.4.13) tiene infinitos equilibrios n = nπ. Si n es par, la masa está directamente debajo del eje (Figura 9.4.4.6 (a)) y la gravedad se opone a cualquier desviación del equilibrio.
Sin embargo, si n es impar, la masa está directamente sobre el eje (Figura 9.4.4.6 (b)) y la gravedad aumenta cualquier desviación del equilibrio. Por lo tanto, concluimos por razones físicas que 2m = 2mπ es estable y 2m + 1 = (2m + 1)π es inestable.
Figura 9.4.4.6 (a) Equilibrio estable (b) Equilibrio inestable
El plano de fase equivalente de (9.4.4.13) es
donde v = y′ es la velocidad angular del péndulo. Integrando esto se obtiene
(9.4.4.14)
Si v = v0 cuando y = 0, entonces
entonces (9.4.4.14) se convierte en
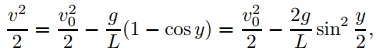
(9.4.4.15)
donde
Las curvas definidas por (9.4.4.15) son las trayectorias de (9.4.4.13). Son periódicas con período 2π en y, lo cual no es sorprendente, ya que si y = y(t) es una solución de (9.4.4.13), entonces también lo es yn = y(t) + 2nπ para cualquier entero n. La figura 9.4.4.7 muestra trayectorias en el intervalo [−π, π]. De (9.4.4.15), puedes ver que si |v0| > vc entonces v es distinto de cero para todo t, lo que significa que el objeto gira en la misma dirección para siempre, como en la figura 9.4.4.8. Las trayectorias asociadas con este movimiento giratorio están por encima de la curva punteada superior y por debajo de la curva punteada inferior en la Figura 9.4.4.7. También puede ver en (9.4.4.15) que si 0 < |v0| < vc, entonces v = 0 cuando y = ±ymax, donde
En este caso el péndulo oscila periódicamente entre −ymax e ymax, como se muestra en la Figura 9.4.4.9. Las trayectorias asociadas con este tipo de movimiento son los óvalos entre las curvas punteadas en la Figura 9.4.4.7. Se puede demostrar (vea el Ejercicio 21 para una demostración parcial) que el período de la oscilación es
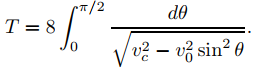(9.4.4.16)
Aunque esta integral no se puede evaluar en términos de funciones elementales familiares, puede ver que es finita si |v0| < vc.
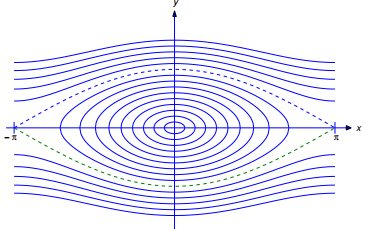
Figura 9.4.4.7 Trayectorias del péndulo no amortiguado
|
Figura 9.4.4.8 El péndulo giratorio no amortiguado |
Figura 9.4.4.9 El péndulo oscilante no amortiguado |
Las curvas discontinuas en la Figura 9.4.4.7 contienen cuatro trayectorias. Los puntos críticos (π, 0) y (−π, 0) son las trayectorias de las soluciones de equilibrio inestable y = ±π. La curva discontinua superior que los conecta (pero no los incluye) se obtiene de las condiciones iniciales de la forma y(t0) = 0, v(t0) = vc. Si y es cualquier solución con esta trayectoria entonces
y 
La curva discontinua inferior que los conecta (pero no los incluye) se obtiene a partir de las condiciones iniciales de la forma y(t0) = 0, v(t0) = −vc. Si y es cualquier solución con esta trayectoria entonces
y 
De acuerdo con esto, la integral (9.4.4.16) diverge a ∞ si v0 = ±vc. (Ejercicio 21) .
Dado que las curvas punteadas separan las trayectorias de las soluciones giratorias de las trayectorias de las soluciones oscilantes, cada una de estas curvas se denomina separadora.
En general, si (9.4.4.7) tiene equilibrios tanto estables como inestables, las separatrices son las curvas dadas por (9.4.4.8) que pasan por puntos críticos inestables. Entonces, si (, 0) es un punto crítico inestable, entonces
(9.4.4.17)
define una separatriz que pasa por (, 0).
Condiciones de Estabilidad e Inestabilidad para y′′ + p(y) = 0
Se puede demostrar (Ejercicio 23) que un equilibrio de una ecuación no amortiguada
y′′ + p(y) = 0 (9.4.4.18)
es estable si hay un intervalo abierto (a, b) que contiene tal que
p(y) < 0 si a < y < y p(y) > 0 si < y < b. (9.4.4.19)
Si consideramos p(y) como una fuerza que actúa sobre una unidad de masa, (9.4.4.19) significa que la fuerza resiste todos los desplazamientos suficientemente pequeños de .
Ya hemos visto ejemplos que ilustran este principio. La ecuación (9.4.4.9) para el sistema masa-resorte no amortiguado tiene la forma (9.4.4.18) con p(y) = ky/m, que tiene solo el equilibrio estable = 0. En este caso (9.4.4.19) se cumple con a = −∞ y b = ∞. La ecuación (9.4.4.13) para el péndulo no amortiguado tiene la forma (9.4.4.18) con p(y) = (g/L) seny. Hemos visto que = 2mπ es un equilibrio estable si m es un número entero. En este caso
p(y) = seny < 0 si (2m − 1)π < y < 2mπ
y
p(y) > 0 si 2mπ < y < (2m + 1)π.
También se puede demostrar (Ejercicio 24) que es inestable si existe un b > tal que
p(y) < 0 si < y < b (9.4.4.20)
O un a < tal que
p(y) > 0 si a < y < . (9.4.4.21)
Si consideramos a p(y) como una fuerza que actúa sobre una unidad de masa, (9.4.4.20) significa que la fuerza tiende a aumentar todos los desplazamientos positivos suficientemente pequeños desde , mientras que (9.4.4.21) significa que la fuerza tiende a aumentar la magnitud de todos los desplazamientos negativos suficientemente pequeños de .
El péndulo no amortiguado también ilustra este principio. Hemos visto que = (2m + 1)π es un equilibrio inestable si m es un número entero. En este caso
seny < 0 si (2m + 1)π < y < (2m + 2)π,
entonces (9.4.4.20) se cumple con b = (2m + 2)π, y
seny > 0 si 2mπ < y < (2m + 1)π,
entonces (9.4.4.21) se cumple con a = 2mπ.
Ejemplo ilustrativo 9.4.4.3
La ecuación
y′′ + y(y − 1) = 0 (9.4.4.22)
es de la forma (9.4.4.18) con p(y) = y(y − 1). Por lo tanto = 0 y = 1 son los equilibrios de (9.4.4.22).
Desde
y(y − 1) > 0 si y < 0 o y > 1,
y(y − 1) < 0 si 0 < y < 1,
= 0 es inestable y = 1 es estable.
El equivalente en el plano de fase de (9.4.4.22) es la ecuación separable
Integrando, obtenemos
La que reescribimos como
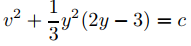(9.4.4.23)
después de renombrar la constante de integración. Estas son las trayectorias de (9.4.4.22). Si y es cualquier solución de (9.4.4.22), el punto (y(t), v(t)) se mueve a lo largo de la trayectoria de y en la dirección de y creciente en el semiplano superior (v = y′ > 0) , o en la dirección decreciente de y en el semiplano inferior (v = y′ < 0).
La Figura 9.4.4.10 muestra trayectorias típicas. La curva punteada que pasa por el punto crítico (0, 0), obtenida al establecer c = 0 en (9.4.4.23), separa el plano y–v en regiones que contienen diferentes tipos de trayectorias; de nuevo, llamamos a esta curva una separatriz. Las trayectorias en la región delimitada por el bucle cerrado (b) son curvas cerradas, por lo que las soluciones asociadas con ellas son periódicas. Las soluciones asociadas con otras trayectorias no son periódicas. Si y es una de esas soluciones con trayectoria que no está en la separatriz, entonces
Figura 9.4.4.10 Trayectorias de y′′ + y(y − 1) = 0
La separatriz contiene cuatro trayectorias de (9.4.4.22). Uno es el punto (0, 0), la trayectoria del equilibrio = 0. Dado que las distintas trayectorias no pueden intersecarse, los segmentos de la separadora marcados (a), (b) y (c), que no incluye (0, 0) – son trayectorias distintas, ninguna de las cuales se puede recorrer en un tiempo finito. Las soluciones con estas trayectorias tienen el siguiente comportamiento asintótico:
El caso amortiguado
El plano de fase equivalente de la ecuación autónoma amortiguada
y′′ + q(y, y′)y′ + p(y) = 0 (9.4.4.24)
es
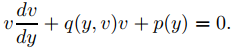
Esta ecuación no es separable, por lo que no podemos resolverla para v en términos de y, como hicimos en el caso no amortiguado, y la conservación de la energía no se cumple. (Por ejemplo, se pierde la energía gastada en vencer la fricción). Sin embargo, podemos estudiar el comportamiento cualitativo de sus soluciones reescribiéndola como
(9.4.4.25)
y considerando los campos direccionales para esta ecuación. En los siguientes ejemplos, también mostraremos trayectorias generadas por computadora de esta ecuación, obtenidas por métodos numéricos. Los ejercicios requieren cálculos similares. Los métodos discutidos en el Capítulo 9.3 no son adecuados para esta tarea, ya que p(y)/v en (9.4.4.25) no está definido en el eje y del plano de fase de Poincaré. Por lo tanto, nos vemos obligados a aplicar métodos numéricos discutidos brevemente en la Sección 9.10.1 al sistema
que es equivalente a (9.4.4.24) en el sentido definido en la Sección 9.10.1. Afortunadamente, la mayoría de los paquetes de software de ecuaciones diferenciales le permiten hacer esto sin problemas.
En el texto nos limitaremos al caso donde q es constante, entonces (9.4.4.24) y (9.4.4.25) se reducen a
y′′ + cy′ + p(y) = 0 (9.4.4.26)
y
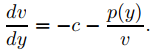
(Consideraremos ecuaciones más generales en los ejercicios). La constante c se llama constante de amortiguamiento. En situaciones donde (9.4.4.26) es la ecuación de movimiento de un objeto, c es positiva; sin embargo, hay situaciones en las que c puede ser negativa.
El sistema de masa-resorte amortiguado
Anteriormente consideramos el sistema resorte-masa bajo la suposición de que las únicas fuerzas que actúan sobre el objeto son la gravedad y la resistencia del resorte a los cambios en su longitud. Ahora supondremos que algún mecanismo (por ejemplo, la fricción en el resorte o la resistencia atmosférica) se opone al movimiento del objeto con una fuerza proporcional a su velocidad. En la Sección 9.6.1 se demostrará que en este caso la segunda ley de movimiento de Newton implica que
my′′ + cy′ + ky = 0, (9.4.4.27)
donde c > 0 es la constante de amortiguamiento. Nuevamente, esta ecuación se puede resolver fácilmente mediante un método que estudiaremos en la Sección 9.5.2, pero ese método no está disponible aquí. En cambio, consideraremos su equivalente en el plano de fase, que se puede escribir en la forma (9.4.4.25) como
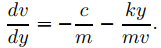(9.4.4.28)
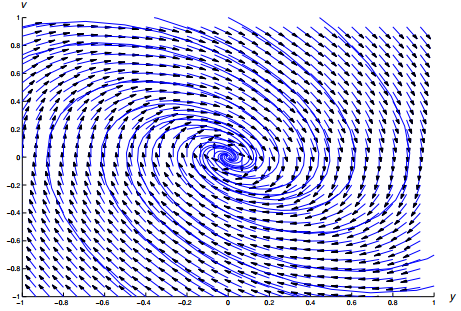
(Una nota menor: la c en (9.4.4.26) en realidad corresponde a c/m en esta ecuación.) La figura 9.4.4.11 muestra un campo direccional típico para una ecuación de esta forma. Si recuerda que el movimiento a lo largo de una trayectoria debe ser en la dirección de aumentar y en el semiplano superior (v > 0) y en la dirección de disminuir y en el semiplano inferior (v < 0), puede inferir que todas las trayectorias se aproximan a la origen en el sentido de las agujas del reloj. Para confirmar esto, la Figura 9.4.4.12 muestra el mismo campo direccional con algunas trayectorias rellenadas. Todas las trayectorias que se muestran allí corresponden a soluciones del problema de valor inicial
my′′ + cy′ + ky = 0, y(0) = y0, y′(0) = v0,
donde
mv02 + ky02 = ρ (una constante positiva);
por lo tanto, si no hubiera amortiguamiento (c = 0), todas las soluciones tendrían la misma trayectoria elíptica discontinua, que se muestra en la Figura 9.4.4.14.
|
Figura 9.4.4.11 Un campo direccional típico para my′′ + cy′ + ky = 0 con 0 < c < c1 |
Figura 9.4.4.12 Figura 4.4.11 con algunas trayectorias añadidas |
|
Figura 9.4.4.13 Una solución oscilatoria de my′′ + cy′ + ky = 0 |
|
|
Figura 9.4.4.14 Un campo direccional típico para my′′ + cy′ + ky = 0 con c > c1 |
|
Las soluciones correspondientes a las trayectorias de la Figura 9.4.4.12 cruzan el eje y infinitas veces. Se dice que las soluciones correspondientes son oscilatorias (Figura 9.4.4.13) En la Sección 9.6.2 se muestra que hay un número c1 tal que si 0 ≤ c < c1 entonces todas las soluciones de (9.4.4.27) son oscilatorias, mientras que si c ≥ c1, ninguna solución de (9.4.4.27) tiene esta propiedad. (De hecho, ninguna solución que no sea idénticamente cero puede tener más de dos ceros en este caso). La figura 9.4.4.14 muestra un campo direccional y algunas curvas integrales para (9.4.4.28) en este caso.
Ejemplo ilustrativo 9.4.4.3 (El péndulo amortiguado)
Ahora volvemos al péndulo. Si suponemos que algún mecanismo (por ejemplo, la fricción en el eje o la resistencia atmosférica) se opone al movimiento del péndulo con una fuerza proporcional a su velocidad angular, la segunda ley de movimiento de Newton implica que
mLy′′ = −cy′ − mgseny, (9.4.4.29)
donde c > 0 es la constante de amortiguamiento. (Nuevamente, una nota menor: la c en (9.4.4.26) en realidad corresponde a c/mL en esta ecuación). Para trazar un campo direccional para (9.4.4.29) escribimos su equivalente en el plano de fase como
La Figura 9.4.4.15 muestra las trayectorias de cuatro soluciones de (9.4.4.29), todas las cuales satisfacen y(0) = 0. Para cada m = 0, 1, 2, 3, impartir la velocidad inicial v(0) = vm hace que el péndulo para hacer m revoluciones completas y luego asentarse en una oscilación decreciente alrededor del equilibrio estable = 2mπ.
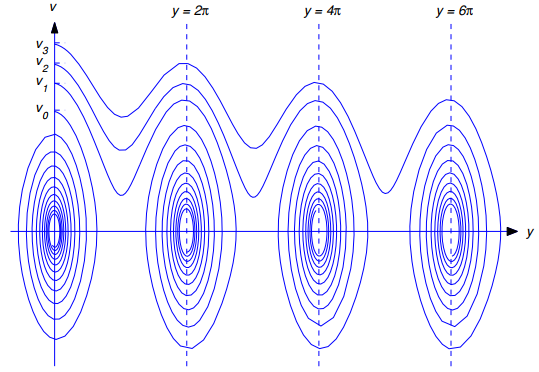
Figura 9.4.4.15 Cuatro trayectorias del péndulo amortiguado