| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.2 |

10.2 Vectores en tres dimensiones

Objetivos de aprendizaje:

10.2.1. Describir el espacio tridimensional matemáticamente.
10.2.2. Ubicar puntos en el espacio usando coordenadas.
10.2.3. Escribir la fórmula de la distancia en tres dimensiones.
10.2.4. Escribir las ecuaciones para planos y esferas simples.
10.2.5. Realizar operaciones vectoriales en R³.

       Los vectores son herramientas útiles para resolver problemas bidimensionales. La vida, sin embargo, ocurre en tres dimensiones. Para expandir el uso de vectores a aplicaciones más realistas, es necesario crear un marco para describir el espacio tridimensional. Por ejemplo, aunque un mapa bidimensional es una herramienta útil para navegar de un lugar a otro, en algunos casos la topografía del terreno es importante. ¿Su ruta planeada va a través de las montañas? ¿Tienes que cruzar un río? Para apreciar completamente el impacto de estas características geográficas, debes usar tres dimensiones. Esta sección presenta una extensión natural del plano de coordenadas cartesianas bidimensional a un sistema de coordenadas de un espacio en tres dimensiones.

Sistemas de coordenadas tridimensionales

Como hemos aprendido, el sistema de coordenadas rectangulares bidimensionales contiene dos ejes perpendiculares: el eje horizontal x y el eje vertical y. Podemos agregar una tercera dimensión, el eje z, que es perpendicular tanto al eje x como al eje y. Llamamos a este sistema el sistema de coordenadas rectangulares tridimensionales. Representa las tres dimensiones que encontramos en la vida real.

Definición 10.1. Sistema de coordenadas rectangulares tridimensionales

El sistema de coordenadas rectangulares tridimensionales consta de tres ejes perpendiculares: el eje x, el eje y y el eje z. Debido a que cada eje es una recta numérica que representa todos los números reales en R, el sistema tridimensional a menudo se denota por R³. ♦

En la figura 10.2_1 (a), el eje z positivo se muestra sobre el plano que contiene los ejes x e y. El eje x positivo aparece a la izquierda y el eje y positivo está a la derecha. Una pregunta natural es: ¿Cómo se determinó el acuerdo? El sistema que se muestra sigue la regla de la mano derecha. Si tomamos nuestra mano derecha y alineamos los dedos con el eje x positivo, luego doblamos los dedos para que apunten en la dirección del eje y positivo, nuestro pulgar apunta en la dirección del eje z positivo. En este texto, siempre trabajamos con sistemas de coordenadas configurados de acuerdo con la regla de la mano derecha. Algunos sistemas siguen una regla de la mano izquierda, pero la regla de la derecha se considera la representación estándar.

Figura 10.2_1 (a) Podemos extender el sistema de coordenadas rectangulares bidimensionales agregando un tercer eje, el eje z, que es perpendicular tanto al eje x como al eje y. (b) La regla de la mano derecha se usa para determinar la ubicación de los ejes de coordenadas en el plano cartesiano estándar.

        En dos dimensiones, describimos un punto en el plano con las coordenadas (x, y). Cada coordenada describe cómo se alinea el punto con el eje correspondiente. En tres dimensiones, se agrega una nueva coordenada, z, para indicar la alineación con el eje z: (x, y, z). Un punto en el espacio se identifica por las tres coordenadas (Figura 10.2_2). Para trazar el punto (x, y, z), vaya x unidades a lo largo del eje x, luego y unidades en la dirección del eje y, luego, z unidades en la dirección del eje z.

Figura 10.2_2 Para trazar el punto (x, y, z) vaya x unidades a lo largo del eje x, luego y unidades en la dirección del eje y, luego z unidades en la dirección del eje z.

Ejemplo ilustrativo 10.2_1. Puntos de localización en el espacio

Localiza el punto (1, −2, 3) en el espacio tridimensional.

Solución:

Para localizar este punto en R³, comience dibujando tres lados de un prisma rectangular a lo largo de los ejes de coordenadas: una unidad en la dirección x positiva, 2 unidades en la dirección y negativa y 3 unidades en la dirección z positiva. Complete el prisma para trazar el punto (Figura 10.2_3).

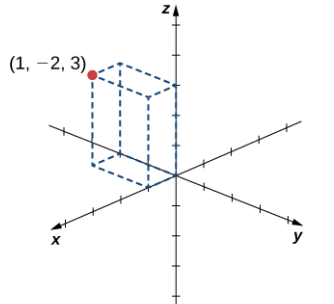
Figura 10.2_3 Dibujando el punto (1, −2, 3). ♦

Ejercicio de control 10.2_1

Dibuja el punto (−2, 3, −1) en un espacio tridimensional. ♦

       En el espacio bidimensional, el plano de coordenadas está definido por un par de ejes perpendiculares. Estos ejes nos permiten nombrar cualquier ubicación dentro del plano. En tres dimensiones, definimos planos de coordenadas por los ejes de coordenadas, tal como en dos dimensiones. Ahora hay tres ejes, por lo que hay tres pares de ejes que se cruzan. Cada par de ejes forma un plano de coordenadas: el plano xy, el plano xz y el plano yz (Figura 10.2_4).

Definimos formalmente el plano xy como el siguiente conjunto: {(x, y, 0): x, y ∈ R}. Del mismo modo, el plano xz y el plano yz se definen como {(x, 0, z): x, z ∈ R} y {(0, y, z): y, z ∈ R}, respectivamente.

Para visualizar esto, imagina que estás construyendo una casa y estás parado en una habitación con solo dos de las cuatro paredes terminadas. (Suponga que las dos paredes terminadas son adyacentes entre sí). Si se para de espaldas a la esquina donde se encuentran las dos paredes terminadas, de frente a la habitación, el piso es el plano xy, la pared a su derecha es el xz-plano, y la pared a su izquierda es el yz-plano.

Figura 10.2_4 El plano que contiene los ejes x e y se llama plano xy. El plano que contiene los ejes x y z se llama plano xz, y los ejes y y z definen el plano yz.

En dos dimensiones, los ejes de coordenadas dividen el plano en cuatro cuadrantes. Del mismo modo, los planos de coordenadas dividen el espacio entre ellos en ocho regiones alrededor del origen, llamadas octantes. Los octantes llenan R³ de la misma manera que los cuadrantes llenan R², como se muestra en la Figura 10.2_5.

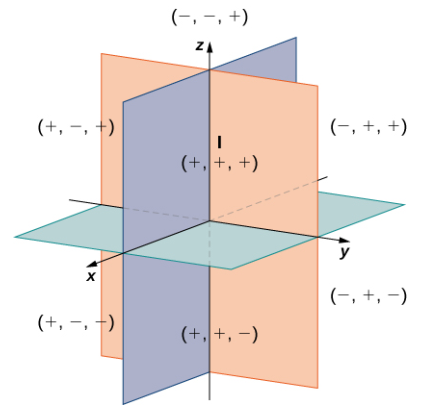
Figura 10.2_5 Los puntos que se encuentran en octantes tienen tres coordenadas distintas de cero.

       La mayoría del trabajo en el espacio tridimensional es una extensión cómoda de los conceptos correspondientes en dos dimensiones. En esta sección, usamos nuestro conocimiento de los círculos para describir las esferas, luego ampliamos nuestra comprensión de los vectores a tres dimensiones. Para lograr estos objetivos, comenzamos adaptando la fórmula de la distancia al espacio tridimensional.

Si dos puntos se encuentran en el mismo plano de coordenadas, entonces es sencillo calcular la distancia entre ellos. Consideramos que la distancia d entre dos puntos (x₁, y₁) y (x₂, y₂) en el plano de coordenadas xy viene dada por la fórmula

La fórmula para la distancia entre dos puntos en el espacio es una extensión natural de esta fórmula.

Teorema 10.2.1. Distancia entre dos puntos en el espacio

♦

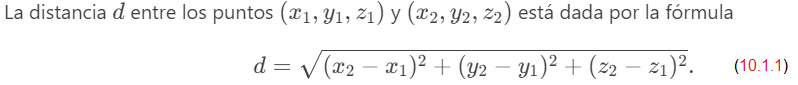
La demostración de este teorema se deja como ejercicio. (Sugerencia: primero encuentre la distancia d₁ entre los puntos (x₁, y₁, z₁) y (x₂, y₂, z₁) como se muestra en la figura 10.2_6)

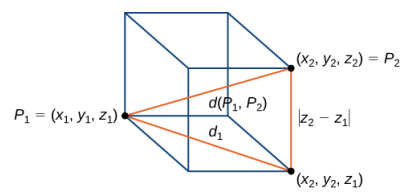
Figura 10.2_6 La distancia entre P₁ y P₂ es la longitud de la diagonal del prisma rectangular que tiene P₁ y P₂ como esquinas opuestas.

Ejemplo ilustrativo 10.2_2. Distancia en el espacio

Encuentre la distancia entre los puntos P₁ = (3, −1, 5) y P₂ = (2, 1, −1).

Solución:

Sustituya los valores directamente en la fórmula de la distancia:

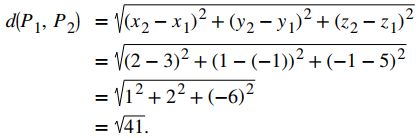
Ejercicio de control 10.2_2

Encuentre la distancia entre los puntos P₁ = (1, −5, 4)  y  P₂ = (4, −1, −1). ♦

       Antes de pasar a la siguiente sección, veamos cómo R³ difiere de R². Por ejemplo, en R², las rectas que no son paralelas siempre deben cruzarse. Este no es el caso en R³. Por ejemplo, considere las rectas en azul y rojo que se muestran en la Figura 10.2_7. Estas dos rectas ni son paralelas, ni se intersecan.

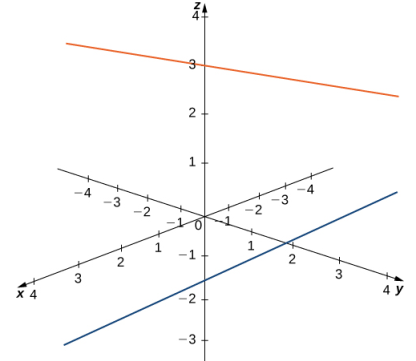
Figura 10.2_7 Estas dos rectas no son paralelas, pero tampoco se intersecan.

R³ también puede tener circunferencias que estén interconectadas pero que no tengan puntos en común, como en la Figura 10.2_8.

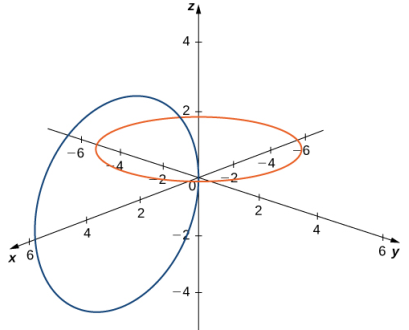
Figura 10.2_8 Estas circunferencias están interconectadas, pero no tienen puntos en común.

Tenemos mucha más flexibilidad trabajando en tres dimensiones que si nos quedamos con solo dos dimensiones.

Escribir ecuaciones en ℝ³

Ahora que podemos representar puntos en el espacio y encontrar la distancia entre ellos, estamos en condiciones de aprender a escribir ecuaciones de objetos geométricos como rectas, planos y superficies curvas en R³. Primero, comenzamos con una ecuación simple. Compare las gráficas de la ecuación x = 0 en R, R² y R³ (Figura 10.2_9). A partir de estos gráficos, podemos ver que la misma ecuación puede describir un punto, una recta o un plano.

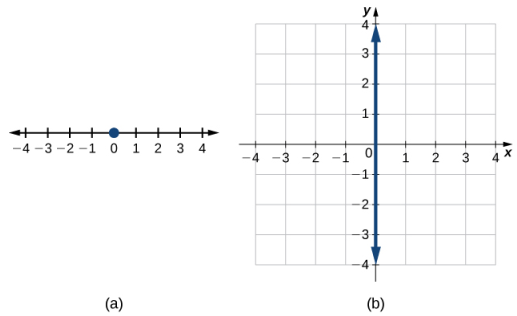
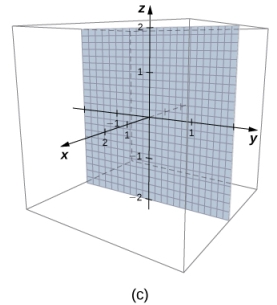
En el espacio, la ecuación x = 0 describe todos los puntos (0, y, z). Esta ecuación define el plano yz. Del mismo modo, el plano xy contiene todos los puntos de la forma (x, y, 0). La ecuación z = 0 define el plano xy y la ecuación y = 0 describe el plano xz (Figura 10.2_10).

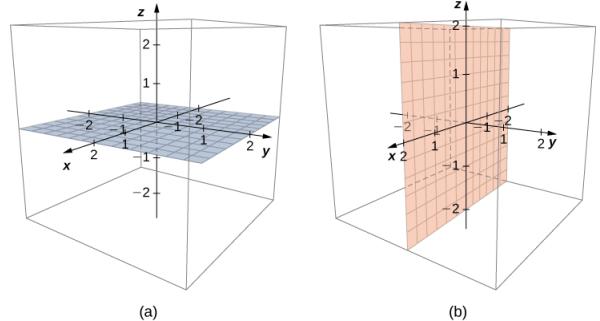
       Comprender las ecuaciones de los planos de coordenadas nos permite escribir una ecuación para cualquier plano que sea paralelo a uno de los planos de coordenadas. Cuando un plano es paralelo al plano xy, por ejemplo, la coordenada z de cada punto en el plano tiene el mismo valor constante. Solo las coordenadas x e y de los puntos en ese plano varían de un punto a otro.

Regla 10.2.1: Ecuaciones de planos paralelos para coordinar planos

1) El plano en el espacio que es paralelo al plano xy y contiene el punto (a, b, c) puede representarse mediante la ecuación

z = c.

2) El plano en el espacio que es paralelo al plano xz y contiene el punto (a, b, c) puede representarse mediante la ecuación

y = b.

3) El plano en el espacio que es paralelo al plano yz y contiene el punto (a, b, c)) puede representarse mediante la ecuación

x = a.

Ejemplo ilustrativo 10.2_3. Escribir ecuaciones de planos paralelos a planos coordinados

a) Escribe una ecuación del plano que pasa por el punto (3, 11, 7) que es paralela al plano yz.

b) Encuentre una ecuación del plano que pasa por los puntos (6, −2, 9), (0, −2, 4) y (1, −2, −3).

Solución:

a) Cuando un plano es paralelo al plano yz, solo las coordenadas y y z pueden variar. La coordenada x tiene el mismo valor constante para todos los puntos en este plano, por lo que este plano puede ser representado por la ecuación x = 3.

b) Cada uno de los puntos (6, −2, 9), (0, −2, 4) y (1, −2, −3) tiene la misma coordenada y. Este plano puede ser representado por la ecuación y = −2. ♦

Ejercicio de control 10.2_3

Escribe una ecuación del plano que pasa por el punto (1, −6, −4) que es paralelo al plano xy. ♦

       Como hemos visto, en R² la ecuación x = 5 describe la recta vertical que pasa por el punto (5, 0). Esta recta es paralela al eje y. En una extensión natural, la ecuación x = 5 en R³ describe el plano que pasa por el punto (5, 0, 0), que es paralelo al plano yz. Otra extensión natural de una ecuación familiar se encuentra en la ecuación de una esfera.

Definición 10.2.2. La esfera

Una esfera es el conjunto de todos los puntos en el espacio equidistantes de un punto fijo, el centro de la esfera (Figura 10.2_11), así como el conjunto de todos los puntos en un plano que son equidistantes del centro representa una circunferencia. En una esfera, como en una circunferencia, la distancia desde el centro hasta un punto de la esfera se llama radio.

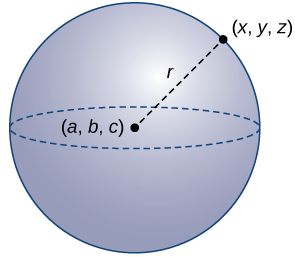
Figura 10.2_11 Cada punto (x, y, z) en la superficie de una esfera está a r unidades del centro (a, b, c). ♦

La ecuación de una circunferencia se deduce usando la fórmula de la distancia en dos dimensiones. Del mismo modo, la ecuación de una esfera se basa en la fórmula tridimensional de la distancia.

Regla 10.2.2: Ecuación de una esfera

La esfera con centro (a, b, c) y radio r puede representarse mediante la ecuación

(x − a)² + (y − b)² + (z − c)²  = r².

 Esta ecuación se conoce como la ecuación estándar de una esfera. ♦

Ejemplo ilustrativo 10.2_4. Hallar la ecuación de una esfera

Encuentre la ecuación estándar de la esfera con centro (10, 7, 4) y punto (−1, 3, −2), como se muestra en la figura 10.2_12.

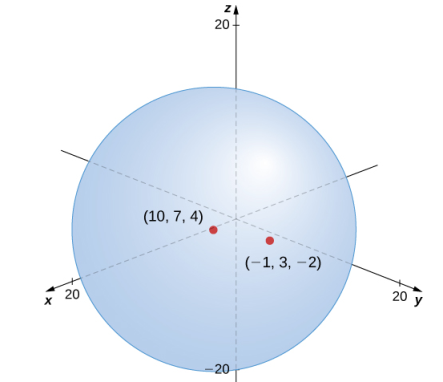
Figura 10.2_12 La esfera centrada en (10, 7, 4) que contiene el punto (−1, 3, −2).

Solución:

Usa la fórmula de la distancia para encontrar el radio r de la esfera:

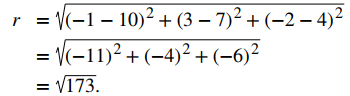
La ecuación estándar de la esfera es

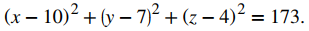
Ejercicio de control 10.2_4

Encuentra la ecuación estándar de la esfera con centro (−2, 4, −5) que contiene el punto (4, 4, −1). ♦

Ejemplo ilustrativo 10.2_5. Hallar la ecuación de una esfera

Supongamos que P = (− 5, 2, 3) y Q = (3, 4, −1), y supongamos además que el segmento de recta PQ forma el diámetro de una esfera (Figura 10.2_13). Encuentra la ecuación de la esfera.

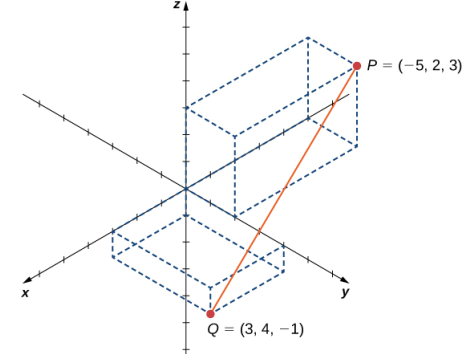
Figura 10.2_13 Segmento de recta PQ.

Solución:

Como PQ es un diámetro de la esfera, sabemos que el centro de la esfera es el punto medio de PQ. Luego,

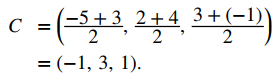
Además, sabemos que el radio de la esfera es la mitad de la longitud del diámetro. Esto da

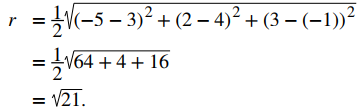
Entonces, la ecuación estándar de la esfera es (x + 1)² + (y − 3)² + (z − 1)² = 21. ♦

Ejercicio de control 10.2_5

Encuentre la ecuación de la esfera con diámetro PQ, donde P = (2, −1, −3) y Q = (− 2, 5, −1). ♦

Ejemplo ilustrativo 10.2_6. Gráfica de ecuaciones en tres dimensiones

Describe el conjunto de puntos en el espacio tridimensional que satisface (x − 2)² + (y − 1)²  = 4, y representa gráficamente el conjunto.

Solución:

Las coordenadas x e y  forman una circunferencia en el plano xy de radio 2, centrado en (2, 1). Como no hay restricción en la coordenada z, el resultado tridimensional es un cilindro circular de radio 2 centrado en la recta con x = 2  e  y = 1. El cilindro se extiende indefinidamente en la dirección z (Figura 10.2_14).

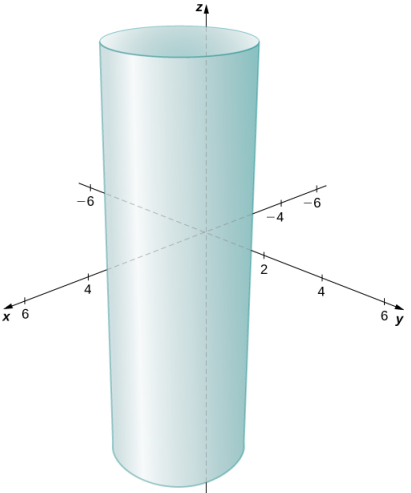
Figura 10.2_14 El conjunto de puntos que satisfacen (x − 2)² + (y − 1)²  = 4. Este es un cilindro de radio 2 centrado en la recta con x = 2 e y = 1. ♦

Ejercicio de control 10.2_6

Describe el conjunto de puntos que satisface (y + 2) (z − 3) = 0 y representa gráficamente el conjunto. ♦

Ejemplo ilustrativo 10.2_7. Gráfica de ecuaciones en tres dimensiones

Describa el conjunto de puntos que satisface (x − 4) (z − 2) = 0, y grafique el conjunto.

Solución:

Debemos tener x − 4 = 0  o  z − 2 = 0, por lo que el conjunto de puntos forma los dos planos x = 4  y  z = 2 (Figura 10.2_15).

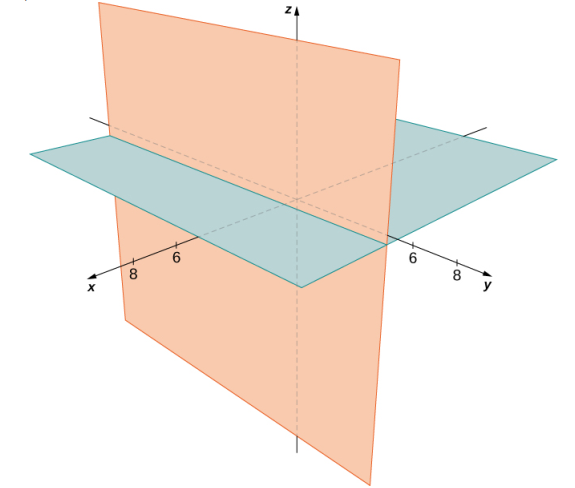
Figura 10.2_15 El conjunto de puntos que satisfacen (x − 4) (z − 2) = 0 forma los dos planos x = 4 y z = 2. ♦

Ejercicio de control 10.2_7

Describe el conjunto de puntos en el espacio tridimensional que satisface x² + (z − 2)² = 16 y haz una gráfica de la superficie. ♦

Trabajando con vectores en ℝ³

Al igual que los vectores bidimensionales, los vectores tridimensionales son cantidades con magnitud y dirección, y están representados por segmentos de recta dirigidos (flechas). Con un vector tridimensional, usamos una flecha tridimensional.

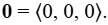Los vectores tridimensionales también se pueden representar en forma de componente. La notación  es una extensión natural del caso bidimensional, que representa un vector con el punto inicial en el origen, (0, 0, 0) y el punto terminal (x,  y,  z) . El vector cero es  Entonces, por ejemplo, el vector tridimensional  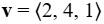está representado por un segmento de recta dirigida desde el punto (0, 0, 0) al punto (2, 4, 1) (Figura 10.2_16).

Figura 10.2_16 El vector está representado por un segmento de recta dirigida desde el punto (0, 0, 0) al punto (2, 4, 1).

       La suma vectorial y la multiplicación escalar se definen de manera análoga al caso bidimensional. Si 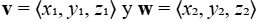 son vectores y si k es un escalar, entonces

 

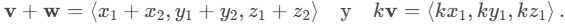
Si k = −1, entonces kv = (−1)v se escribe como −v, y la resta vectorial se define por v − w = v + (−w) = v + (−1)w.

Los vectores unitarios estándar también se extienden fácilmente en tres dimensiones: 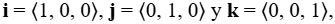 y los usamos en la misma forma en que usamos los vectores unitarios estándar en dos dimensiones. Por lo tanto, podemos representar un vector en R³ de la siguiente manera:

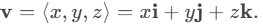
Ejemplo ilustrativo 10.2_8. Representaciones vectoriales

Sea 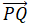 el vector con el punto inicial P = (3, 12, 6) y el punto terminal Q = (−4, −3, 2) como se muestra en la Figura 10.2_17. Exprese  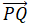en forma de componentes y utilizando vectores unitarios estándar.

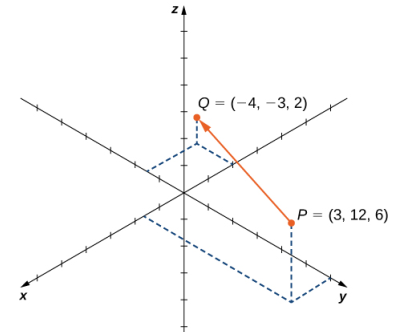
Figura 10.2_17 El vector con el punto inicial P = (3, 12, 6) y el punto terminal Q = (−4, −3, 2)

Solución:

En forma de componente,

En forma unitaria estándar,

Ejercicio de control 10.2_8

       Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. La interpretación geométrica de la suma de vectores, por ejemplo, es la misma en el espacio bidimensional y tridimensional (figura 10.2_18).

(Figura 10.2_18 Para sumar vectores en tres dimensiones, seguimos los mismos procedimientos que aprendimos para dos dimensiones.)

       Ya hemos visto cómo algunas de las propiedades algebraicas de los vectores, como la suma de vectores y la multiplicación escalar, pueden extenderse a tres dimensiones. Otras propiedades pueden ampliarse de manera similar. Se resumen aquí para nuestra referencia.

Regla 10.2.3: Propiedades de los vectores en el espacio

       Ya sabemos que la adición de vectores en dos dimensiones satisface las propiedades conmutativas, asociativas e inversa aditiva. Estas propiedades de las operaciones vectoriales también son válidas para vectores tridimensionales. La multiplicación escalar de vectores satisface la propiedad distributiva, y el vector cero actúa como una identidad aditiva. Las pruebas para verificar estas propiedades en tres dimensiones son extensiones directas de las pruebas en dos dimensiones.

Ejemplo ilustrativo 10.2_9. Operaciones vectoriales en tres dimensiones

Sea 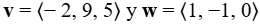 (Figura 10.2_19). Encuentra los siguientes vectores.

a) 3v − 2w

b) 5∥w∥

c) ∥5w∥

d) Un vector unitario en la dirección de v.

Solución:

a) Primero, use la multiplicación escalar de cada vector, luego reste:

b) Escribe la ecuación para la magnitud del vector, luego usa la multiplicación escalar:

c) Primero, use la multiplicación escalar, luego encuentre la magnitud del nuevo vector. Tenga en cuenta que el resultado es el mismo que para la parte b.:

d) Recuerde que para encontrar un vector unitario en dos dimensiones, dividimos el vector por su magnitud. El procedimiento es el mismo en tres dimensiones:

Ejercicio de control 10.2_9

Sean los vectores 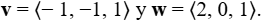 Encuentre un vector unitario en la dirección de 5v + 3w. ♦

Ejemplo ilustrativo 10.2_10. Lanzar un pase hacia adelante

Un mariscal de campo está de pie en el campo de fútbol preparándose para lanzar un pase. Su receptor está parado 20 yardas por el campo y 15 yardas a la izquierda del mariscal de campo. El mariscal de campo lanza la pelota a una velocidad de 60 mph hacia el receptor en un ángulo ascendente de 30° (ver la siguiente figura). Escriba el vector de velocidad inicial de la pelota, v, en forma de componente.

Solución:

Lo primero que debemos hacer es encontrar un vector en la misma dirección que el vector de velocidad de la pelota. Luego escalamos el vector apropiadamente para que tenga la magnitud correcta. Considere el vector w que se extiende desde el brazo del mariscal de campo hasta un punto directamente sobre la cabeza del receptor en un ángulo de 30° (vea la siguiente figura). Este vector tendría la misma dirección que v, pero puede no tener la magnitud correcta.

El receptor está 20 yardas abajo del campo y 15 yardas a la izquierda del mariscal de campo. Por lo tanto, la distancia en línea recta desde el mariscal de campo al receptor es

Tenemos 25/∥w∥ = cos30°. Entonces la magnitud de w viene dada por

y la distancia vertical desde el receptor hasta el punto terminal de w es

Entonces w = ⟨20, 15, 25/ √3⟩, y tiene la misma dirección que v.

Sin embargo, recuerde que calculamos que la magnitud de w es ∥w∥ = 50√3, y que v tiene una magnitud de 60 mph. Entonces, necesitamos multiplicar el vector w por una constante apropiada, k. Queremos encontrar un valor de k para que ∥kw∥ = 60 mph. Tenemos

entonces queremos

Entonces

Vuelva a verificar que ∥v∥ = 60. Tenemos

De tal manera que, hemos encontrado los componentes correctos para v.

Ejercicio de control 10.2_10

Suponga que el mariscal de campo y el receptor están en el mismo lugar que en el ejemplo anterior. Esta vez, sin embargo, el mariscal de campo lanza la pelota a una velocidad de 40 mph y un ángulo de 45°. Escriba el vector de velocidad inicial de la pelota, v, en forma de componentes. ♦