| 1. Funciones y sus gráficas | 1.1. Revisión de funciones |
Ejercicios resueltos del Capítulo 1.1
Cálculo de Zill
Pulse sobre el ejercicio deseado para que observe la solución en imagen o en video. 👀
Zill 1.1_1 a 6 En los problemas 1–6, encuentre los valores funcionales indicados:
Zill 1.1_7 y 8 En los problemas 7 y 8, encuentre
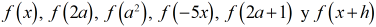
Zill 1.1_9 ¿Para qué valores de x, f (x) = 6x² − 1 es igual a 23?
Zill 1.1_10 ¿Para qué valores de x, f (x) = √(x − 4) es igual a 4?
Zill 1.1_11 a 26 En los problemas 11–26, encuentre el dominio de la función
f dada:
Soluciones en imagen

Solución – Juan Beltrán:
f (x)= –2x² + x (1)
Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:


Solución – Juan Beltrán:

Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:

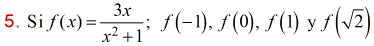
Solución – Juan Beltrán:

Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:


Solución – Juan Beltrán:

Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:
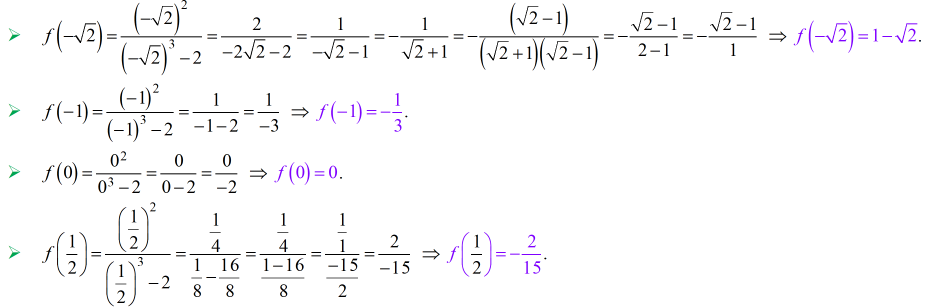

Solución – Juan Beltrán:

Zill 1.1_10 ¿ Para qué valores de x, f (x) = √(x − 4) es igual a 4?
Solución – Juan Beltrán:
Se debe resolver la siguiente ecuación


Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no son números reales, debemos resolver la siguiente inecuación:


Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no existen en los reales, debemos resolver la siguiente inecuación:


Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no existen en los reales y que la división por 0 no tiene sentido, la fórmula que involucra la variable independiente x debe cumplir las siguientes dos condiciones:

que se resumen en esta única condición:
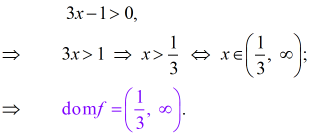

Solución – Juan Beltrán:
Para evitar la división por cero se debe satisfacer la siguiente condición:


Solución – Juan Beltrán:
Para evitar la división por cero se debe satisfacer la siguiente condición:

Para los siguientes ejercicios, observando la tabla de valores respectiva, (a) determine el dominio y
el rango de cada relación, y (b) indique si la relación
es o no una función.
Ejercicio 1
| x | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Ejercicio 2
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
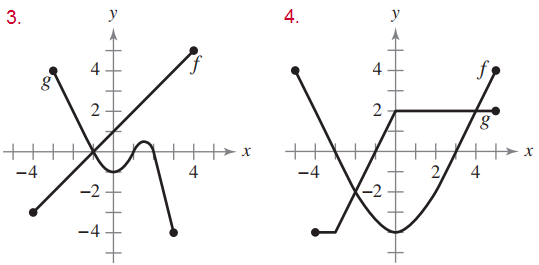
En los ejercicios 3 y 4, utiliza las gráficas de f y g para responder lo siguiente:
a) Identifica el dominio y el rango de f y g.
b) Identifica f (-2) y g (3).
c) ¿Para qué valores de x es f (x) = g (x)?
d) Calcula las soluciones de f (x) = 2.
e) Calcula las soluciones de g (x) = 0.
Ejercicio 5. Determine si los números 1, 5 y 8 están en el rango de la siguiente función definida por tramos:
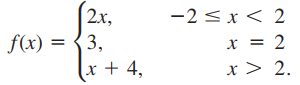
En los ejercicios 6 y 7, evalúe (si es posible) la función en los valores dados de la variable independiente. Simplificar los resultados.
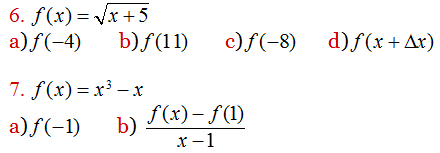
En los ejercicios 8 a 10, encuentre el dominio de la función dada:
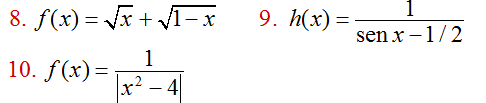
En los ejercicios 11 y 12, halle el dominio, el rango y todos ceros / intersecciones, si las hay, de las funciones dadas:
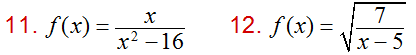
En los ejercicios 13 y 14, para cada par de funciones, encuentre
- a) f + g b) f – g c) f g d) f / g.
Determinar el dominio de cada una de estas nuevas funciones.
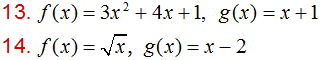
En los ejercicios 15 y 16, para cada par de funciones, encuentre
a) (f ∘ g)(x) y b) (g ∘ f)(x) Simplifique los resultados.
Encuentre el dominio de cada uno de las funciones compuestas obtenidas:
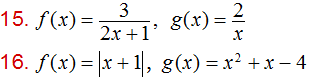
« Capítulo 1.1: Revisión de funciones
Ejercicios propuestos del Capítulo 1.1 »






Muy práctica toda la información de ésta página, recomendable para repaso de cálculo…
Bienvenido!