| 7. Sucesiones y series infinitas | Ejercicios propuestos para el Capítulo 7.3 |
7.3 PRUEBAS DE LA DIVERGENCIA Y DE LA INTEGRAL
Objetivos de aprendizaje:
7.3.1. Usar la prueba de la divergencia para determinar si una serie converge o diverge.
7.3.2. Usar la prueba de la integral para determinar la convergencia de una serie.
7.3.3. Estimar el valor de una serie encontrando límites para el resto o residuo.
En la sección anterior, determinamos la convergencia o divergencia de varias series calculando explícitamente el límite de la sucesión de sumas parciales {Sk}. En la práctica, calcular explícitamente este límite puede ser difícil o imposible. Afortunadamente, existen varias pruebas que nos permiten determinar la convergencia o divergencia para muchos tipos de series. En esta sección, discutimos dos de estas pruebas: la prueba de la divergencia y la prueba de la integral. Examinaremos varias otras pruebas en el resto de este capítulo y luego resumiremos cómo y cuándo usarlas.
Prueba de la divergencia
Para que una serie  converja, el enésimo término an debe satisfacer an → 0 cuando n → ∞.
converja, el enésimo término an debe satisfacer an → 0 cuando n → ∞.
Observemos que a partir de las propiedades algebraicas de límites para sucesiones,

Por lo tanto, si  converge, el enésimo término an → 0 cuando n → ∞. Una consecuencia importante de este hecho es la siguiente afirmación:
converge, el enésimo término an → 0 cuando n → ∞. Una consecuencia importante de este hecho es la siguiente afirmación: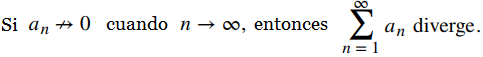
Esta prueba se conoce como prueba de la divergencia porque proporciona una forma de demostrar que una serie diverge.
Teorema 7.3_1. Prueba de la divergencia
Si \( \lim\limits_{n \to \infty} a_n = c \neq 0 \) o \( \lim\limits_{n \to \infty} a_n \) no existe, entonces la serie \( \sum\limits_{n=1}^{\infty} a_n \) diverge.Es importante señalar que el recíproco de este teorema no es cierto. Es decir, si limn → ∞ an = 0, no podemos hacer ninguna conclusión sobre la convergencia de

Por ejemplo, limn → ∞ (1/n) = 0, pero la serie armónica

diverge.
En esta sección y en las secciones restantes de este capítulo, mostramos muchos más ejemplos de tales series. En consecuencia, aunque podemos usar la prueba de la divergencia para mostrar que una serie diverge, no podemos usarla para demostrar que una serie converge. Específicamente, si an → 0, la prueba de divergencia no es concluyente.
EJEMPLO ILUSTRATIVO 7.3_1. Usando la prueba de la divergencia
Para cada una de las siguientes series, aplique la prueba de la divergencia. Si la prueba de divergencia demuestra que la serie diverge, indíquelo. De lo contrario, subraye que la prueba de divergencia no es concluyente.

Solución:
a. Dado que n / (3n − 1) → 1/3 ≠ 0, mediante la prueba de divergencia, podemos concluir que

diverge
b. Como 1 / n³ → 0, la prueba de divergencia no es concluyente.
c. Dado que

de acuerdo con la prueba de divergencia, la serie

diverge. ♦
Ejercicio de control 7.3.1
¿Qué nos dice la prueba de divergencia sobre la serie \( \sum\limits_{n=1}^{\infty} \cos\left(\frac{1}{n^2}\right) \)?♦
Prueba de la integral
En la sección anterior, demostramos que la serie armónica diverge observando la sucesión de sumas parciales {Sk} y mostrando que \( S_{2k} > 1 + \frac{k}{2} \) para todos los enteros positivos k (observe la demostración). En esta sección usamos una técnica diferente para probar la divergencia de las series armónicas. Esta técnica es importante porque se utiliza para demostrar la divergencia o convergencia de muchas otras series. Esta prueba, llamada prueba de la integral, compara una suma infinita con una integral impropia. Es importante tener en cuenta que esta prueba solo se puede aplicar cuando consideramos una serie cuyos términos son todos positivos.
Para ilustrar cómo funciona la prueba de la integral, usaremos la serie armónica como ejemplo. En la figura 7.3_1, representamos la serie armónica dibujando una secuencia de rectángulos con áreas 1, 1/2, 1/3, 1/4, … junto con la función f(x) = 1/x. De la gráfica, vemos que

Por lo tanto, para cada k, la k-ésima suma parcial Sk satisface

Como limk → ∞ ln(k + 1) = ∞, vemos que la sucesión de sumas parciales {Sk} no tiene límites. Por lo tanto, {Sk} diverge y, en consecuencia, la serie

también diverge.
vv
(Figura 7.3_1 La suma de las áreas de los rectángulos es mayor que el área entre la curva de f(x) = 1/x y el eje x para x ≥ 1. Como el área delimitada por la curva es infinita (calculada por una integral impropia), la suma de las áreas de los rectángulos también es infinita.)
Ahora considere la serie

Mostramos cómo se puede usar una integral para demostrar que esta serie converge. En la figura 7.3_2, dibujamos una secuencia de rectángulos con áreas 1, 1/ 2², 1/ 3², … junto con la función f (x) = 1 / x². De acuerdo con la gráfica observamos que

Por lo tanto, para cada k, la k ésima suma parcial Sk satisface

Concluimos que la secuencia de sumas parciales {Sk} está acotada. También vemos que {Sk} es una secuencia creciente:

Dado que {Sk} es creciente y acotada, por el Teorema de convergencia monótona, converge. Por lo tanto, la serie

converge.

(Figura 7.3_2 La suma de las áreas de los rectángulos es menor que la suma del área del primer rectángulo y el área entre la curva f (x) = 1/x² y el eje x para x ≥ 1. Como el área delimitada por la curva es finita, la suma de las áreas de los rectángulos también es finita.)
Podemos extender esta idea para probar la convergencia o divergencia de muchas series diferentes. Suponga que

es una serie con términos positivos y tal que existe una función continua, positiva y decreciente f donde f (n) = an para todos los enteros positivos. Luego, como se ilustra en la figura 7.3_3 (a), para cualquier entero positivo k, la k-ésima suma parcial Sk satisface

Por lo tanto, si

converge, entonces la secuencia de sumas parciales {Sk} está acotada. Dado que {Sk} es una secuencia creciente, si además es una secuencia acotada, entonces, según el Teorema de convergencia monótona, converge. Conclusión, si converge, entonces la serie
converge, entonces la serie
también converge. Por otro lado, de la figura 7.3_3 (b), para cualquier entero positivo k, la k-ésima suma parcial Sk cumple





 |
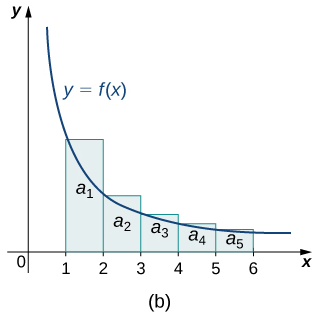 |
| (Figura 7.3_3 (a) Si podemos inscribir rectángulos dentro de una región delimitada por una curva y = f (x) y el eje x, y el área delimitada por esas curvas para x ≥ 1 es finita, entonces la suma de las áreas de los rectángulos también es finita. (b) Si un conjunto de rectángulos circunscribe la región limitada por y = f (x) y el eje x para x ≥ 1 y la región tiene un área infinita, entonces la suma de las áreas de los rectángulos también es infinita.) | |
TEOREMA 7.3_1. Prueba de la integral
Suponga que \( \sum_{n=1}^\infty \mathit{a}_n \) es una serie con términos positivos \( \mathit{a}_n \). Suponga que existe una función \( \mathit{f} \) y un entero positivo \( \mathit{N} \) tales que se cumplen las siguientes tres condiciones: \[ \begin{aligned} &\quad \, i. \quad \mathit{f} \text{ es continua,} \\[5pt] &\quad \, ii. \quad \mathit{f} \text{ es decreciente, y} \\[5pt] &\quad \, iii. \quad \mathit{f}(n) = \mathit{a}_n \text{ para todos los enteros } n \geq \mathit{N}. \end{aligned} \] Entonces \[ \sum_{n=1}^\infty \mathit{a}_n \quad \text{y} \quad \int_{\mathit{N}}^{\infty} \mathit{f}(x) \, dx \] ambas convergen o ambas divergen (ver Figura 7.3_3).♦
Aunque la convergencia de implica la convergencia de las series relacionadas
implica la convergencia de las series relacionadas , esto no implica que el valor de la integral y la serie sean iguales. Pueden ser diferentes, y a menudo lo son. Por ejemplo,
, esto no implica que el valor de la integral y la serie sean iguales. Pueden ser diferentes, y a menudo lo son. Por ejemplo,
es una serie geométrica con término inicial a = 1/e y relación r = 1/e, que converge a Sin embargo, la integral relacionada
Sin embargo, la integral relacionada satisface
satisface
EJEMPLO ILUSTRATIVO 7.3_2. Usando la Prueba de la Integral
Para cada una de las siguientes series, use la prueba integral para determinar si la serie converge o diverge.

Solución:
a. Comparar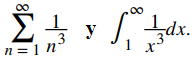 Nosotros tenemos
Nosotros tenemos Así la integral
Así la integral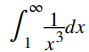 converge, y por lo tanto también lo hace la serie
converge, y por lo tanto también lo hace la serie
b. Comparar Ya que
Ya que la integral
la integral diverge, y por lo tanto, la serie
diverge, y por lo tanto, la serie diverge. ♦
diverge. ♦
Ejercicio de control 7.3.2
Utilice la prueba de la integral para determinar si la serie \( \sum_{n=1}^{\infty} \frac{n}{n^2+1} \) converge o diverge.♦
La serie p
La serie armónica
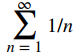
y la serie
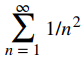
son ejemplos de un tipo de serie llamada serie p.
DEFINICIÓN 7.3_1. Serie p
Para cualquier número real \( p \), la serie \[ \sum_{n=1}^{\infty} \frac{1}{n^{\,p}} \] se llama serie \( p \).♦
Sabemos que la serie p converge si p = 2 y diverge si p = 1. ¿Qué pasa con otros valores de p? En general, es difícil, si no imposible, calcular el valor exacto de la mayoría de las series p. Sin embargo, podemos usar las pruebas presentadas hasta ahora para probar si una serie p converge o diverge.
Si p < 0, entonces 1/nᴾ → ∞, y si p = 0, entonces 1/nᴾ → 1. Por lo tanto, de acuerdo con la prueba de la divergencia,
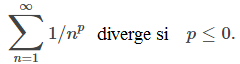
Si p > 0, entonces f (x) = 1/xᴾ es una función positiva, continua y decreciente. Por lo tanto, para p > 0, usamos la prueba de la integral, comparando
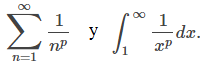
Ya hemos considerado el caso cuando p = 1. Aquí consideramos el caso cuando p > 0, p ≠ 1. Para este caso,
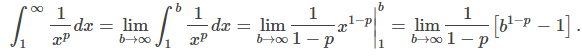
Dado que
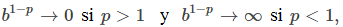
concluimos que
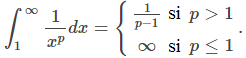
Por lo tanto,

converge si p > 1 y diverge si 0 < p < 1.
En resumen,

EJEMPLO ILUSTRATIVO 7.3_3. Prueba de convergencia de una serie p
Para cada una de las siguientes series, determine si converge o diverge.
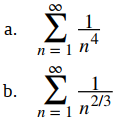
Solución:
a. Esta es una serie p con p = 4 > 1, por lo que la serie converge.
b. Como p = 2/3 < 1, la serie diverge. ♦
Ejercicio de control 7.3.3
¿La serie \( \sum_{n=1}^\infty \frac{1}{\mathit{n}^{5/4}} \) converge o diverge?♦
Estimando el valor de una serie
Supongamos que sabemos que una serie
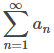
converge y queremos estimar la suma de esa serie. Ciertamente podemos aproximar esa suma usando cualquier suma finita
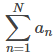
donde N es cualquier número entero positivo. La pregunta que abordamos aquí es, para una serie convergente
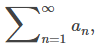
que tan buena es la aproximación
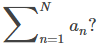
Más específicamente, si dejamos que
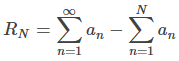
sea el residuo cuando la suma de una serie infinita se aproxima por la enésima suma parcial, ¿qué tan grande es RN? Para algunos tipos de series, podemos usar las ideas de la prueba de la integral para estimar RN.
TEOREMA 7.3_2. Estimación del residuo en la prueba de la integral
Supongamos que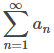 es una serie convergente con términos positivos. Además supongamos que existe una función f que satisface las siguientes tres condiciones:
es una serie convergente con términos positivos. Además supongamos que existe una función f que satisface las siguientes tres condiciones:
i. f es continua,
ii. f está decreciendo, y
iii. f (n) = an para todos los enteros n ≥ 1.
Sea SN la enésima suma parcial de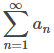
Para todos los enteros positivos N,
\[ S_N + \int_{N+1}^\infty f(x) \, dx < \sum_{n=1}^\infty a_n < S_N + \int_{N}^\infty f(x) \, dx \]En otras palabras, el residuo
\[ R_N = \sum_{n=1}^\infty a_n \, – \, S_N = \sum_{n=N+1}^\infty a_n \]satisface la siguiente estimación:
\[ \int_{N+1}^\infty f(x) \, dx < R_N < \int_{N}^\infty f(x) \, dx \]Esto se conoce como la estimación del residuo. ♦
Ilustramos la estimación del residuo en la prueba de la integral en la figura 7.3_4. En particular, al representar el resto RN = aN + 1 + aN + 2 + aN + 3 + ⋯ como la suma de las áreas de los rectángulos, vemos que el área de esos rectángulos está acotada por arriba por
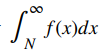
y acotada por abajo por
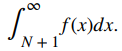
En otras palabras,
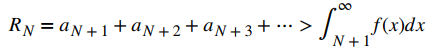
y
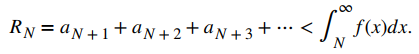
Concluimos que
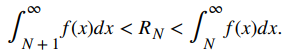
Ya que

donde SN es la enésima suma parcial, concluimos que

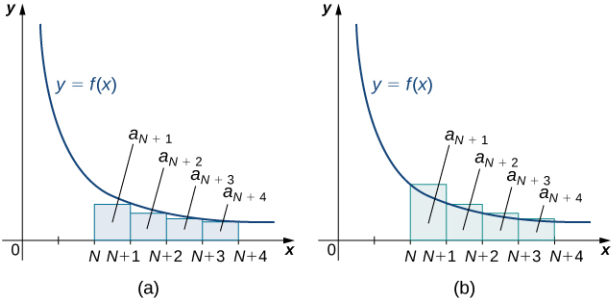
Figura 7.3_4 Dada una función continua, positiva y decreciente f, y una secuencia de términos positivos an tal que an = f (n) para todos los enteros positivos n,
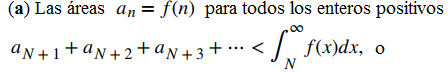
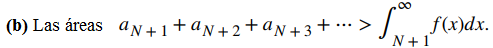
Por lo tanto, la integral es una sobreestimación o una subestimación del error.
EJEMPLO ILUSTRATIVO 7.3_4. Estimando el valor de una serie
Considere la serie
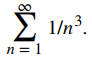
a. Calcule

y estime el error.
b. Determine el menor valor de N necesario de modo que SN estimará
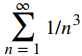
hasta dentro de 0.001.
Solución:
a. Usando una calculadora, obtenemos
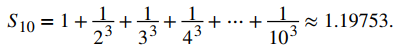
Según la estimación del residuo, sabemos que
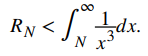
Tenemos que
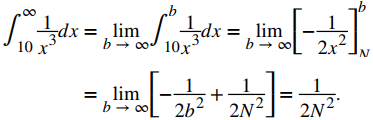
Por lo tanto, el error es R10 <1/2(10)² = 0.005.
b. Encuentre N tal que RN < 0.001. En la parte a. mostramos que RN < 1 / 2N². Por lo tanto, el resto RN <0.001 siempre que 1/2N² < 0.001. Es decir, necesitamos 2N² > 1000. Al resolver esta desigualdad para N, vemos que necesitamos N > 22.36. Para garantizar que el resto esté dentro de la cantidad deseada, debemos redondear al entero más cercano. Por lo tanto, el valor mínimo necesario es N = 23. ♦
Ejercicio de control 7.3.4
Para la serie \( \sum_{n=1}^\infty \frac{1}{\mathit{n}^4} \), calcule \( \mathit{S}_5 \) y estime el error \( \mathit{R}_5 \).♦

Explicación muy clara y completa. Excelente la resolción de ejemplos pertinentes.