Álgebra lineal con aplicaciones
| 1. Sistema de ecuaciones lineales | Ejercicios resueltos del Capítulo 1.2 |
1.2 Eliminación gaussiana
El método algebraico presentado en la sección anterior se puede resumir de la siguiente manera: dado un sistema de ecuaciones lineales, use una secuencia de operaciones elementales de fila para llevar a cabo la matriz aumentada a una matriz “agradable” (lo que significa que las ecuaciones correspondientes son fáciles de resolver). En el Ejemplo 1.1.3, la matriz aumentada del sistema original tomó al final la bonita forma

Las siguientes definiciones identifican las bonitas matrices que surgen en este proceso.
Definición 1.2.1 Forma escalonada por renglón (reducida)
Se dice que una matriz está en forma escalonada por renglones (y se llamará matriz escalonada por renglones) si cumple las siguientes tres condiciones:
1. Todas las filas cero (filas con todos sus elementos iguales a 0) están en la parte inferior.
2. La primera entrada distinta de cero desde la izquierda en cada fila distinta de cero es un 1, llamada el 1 inicial para esa fila.
3. Cada 1 inicial está a la derecha de todos los 1 iniciales en las filas superiores.
Se dice que una matriz escalonada por filas (o renglones) está en forma escalonada reducida por filas (y se llamará matriz escalonada reducida por filas) si, además, cumple la siguiente condición:
4. Cada 1 inicial es la única entrada distinta de cero en su columna. ♦
Las matrices escalonadas tienen una forma de “escalera”, como se indica en el siguiente ejemplo (los asteriscos indican números arbitrarios).

Los primeros 1 proceden “hacia abajo y hacia la derecha” a través de la matriz. Las entradas de arriba y a la derecha de los primeros 1 son arbitrarias, pero todas las entradas de abajo y a la izquierda de ellas son cero. Además, una matriz en forma escalonada por fila está en forma reducida si, adicionalmente, las entradas directamente encima de cada 1 inicial son todas cero. Tenga en cuenta que en una matriz en forma escalonada por fila se pueden realizar algunas operaciones de fila más y llevarse a la forma escalonada reducida (use operaciones de fila para crear ceros sobre cada 1 inicial).
Ejemplo ilustrativo 1.2_1
Las siguientes matrices están en forma escalonada por fila (para cualquier elección de números en posiciones ∗).

Las siguientes matrices, por otro lado, están en forma escalonada reducida

La elección de las posiciones para los primeros 1 determina la forma escalonada (reducida) por fila (aparte de los números en las posiciones ∗). ◊
La importancia de las matrices en la forma escalonada reducida por filas proviene del siguiente teorema.
Teorema 1.2.1
| Cada matriz se puede llevar a una forma escalonada (reducida) mediante una secuencia de operaciones elementales de fila. |
De hecho, podemos dar un procedimiento paso a paso para encontrar una matriz escalonada. Observe que si bien hay muchas secuencias de operaciones de fila que traerán una matriz a la forma escalonada por fila, la que utilizamos es sistemática y fácil de programar en una computadora. Tenga en cuenta que el algoritmo trata con matrices en general, posiblemente con columnas de ceros.
Algoritmo Gaussiano
Paso 1. Si la matriz consiste completamente en ceros, deténgase, ya está en forma escalonada por fila.
Paso 2. De lo contrario, busque la primera columna de la izquierda que contiene una entrada distinta de cero (llámela a) y mueva la fila que contiene esa entrada a la posición superior.
Paso 3. Ahora multiplique la nueva fila superior por 1/a para crear un 1 inicial.
Paso 4. Al restar los múltiplos de esa fila de las filas debajo de ella, haga que cada entrada debajo de este 1 inicial sea 0.
Esto completa la primera fila, y todas las operaciones de fila adicionales se llevan a cabo en las filas restantes
Paso 5. Repita los pasos 1 a 4 en la matriz que consiste en las filas restantes.
El proceso se detiene cuando no quedan filas en el paso 5 o las filas restantes consisten completamente en ceros. ♦
Observe que el algoritmo gaussiano es recursivo: cuando se obtiene el primer 1 inicial, el procedimiento se repite en las filas restantes de la matriz. Esto hace que el algoritmo sea fácil de usar en una computadora. Tenga en cuenta que la solución al Ejemplo 1.1.3 no utilizó el algoritmo gaussiano como está escrito porque el primer 1 inicial no se creó dividiendo la fila 1 por 3. La razón de esto es que evita las fracciones.
Sin embargo, el patrón general es claro: cree los primeros 1s de izquierda a derecha, utilizando cada uno de ellos a su vez para crear ceros debajo de él. Aquí hay dos ejemplos más.
Ejemplo ilustrativo 1.2_2
Resuelve el siguiente sistema de ecuaciones.

Solución:
La matriz aumentada correspondiente es

Cree el primer 1 intercambiando las filas 1 y 2

Ahora reste 3 veces la fila 1 de la fila 2, y reste 4 veces la fila 1 de la fila 3. El resultado es

Ahora resta la fila 2 de la fila 3 para obtener

Esto significa que el siguiente sistema reducido de ecuaciones

es equivalente al sistema original. En otras palabras, los dos tienen las mismas soluciones. Pero este último sistema claramente no tiene solución (la última ecuación requiere que x, y y z satisfagan 0x + 0y + 0z = −3, y no existen tales números). Por lo tanto, el sistema original no tiene solución. ◊
Ejemplo ilustrativo 1.2_3
Resuelve el siguiente sistema de ecuaciones.
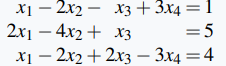
Solución:
La matriz aumentada es

Restar dos veces la fila 1 de la fila 2 y restar la fila 1 de la fila 3 da

Ahora resta la fila 2 de la fila 3 y multiplica la fila 2 por 1/3 para obtener

Esta última matriz está en la forma escalonada, y la llevamos a la forma escalonada reducida agregando la fila 2 a la fila 1:

El correspondiente sistema reducido de ecuaciones es

Los 1s iniciales están en las columnas 1 y 3, por lo que las variables correspondientes x₁ y x₃ se denominan variables principales. Debido a que la matriz está en la forma escalonada reducida, estas ecuaciones se pueden usar para resolver las variables principales en términos de las variables no principales x₂ y x₄. Más precisamente, en el presente ejemplo establecemos x₂ = s y x₄ = t donde s y t son arbitrarias, por lo que estas ecuaciones se convierten en
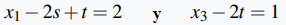
Finalmente las soluciones están dadas por

donde s y t son arbitrarias. ◊
La solución del Ejemplo 1.2.3 es típica del caso general. Para resolver un sistema lineal, la matriz aumentada se lleva a la forma escalonada reducida, y las variables correspondientes a los unos iniciales se denominan variables principales. Debido a que la matriz está en forma reducida, cada variable principal ocurre exactamente en una ecuación, de modo que la ecuación se puede resolver para dar una fórmula para la variable principal en términos de las variables no principales. Es habitual llamar a las variables no principales variables “libres” y etiquetarlas por nuevas variables s, t, …, llamadas parámetros. Por lo tanto, como en el Ejemplo 1.2.3, cada variable xᵢ viene dada por una fórmula en términos de los parámetros s y t. Además, cada elección de estos parámetros conduce a una solución para el sistema, y cada solución surge de esta manera. Este procedimiento funciona en general y ha llegado a llamarse Eliminación gaussiana.
Eliminación gaussiana
Para resolver un sistema de ecuaciones lineales proceda de la siguiente manera:
1. Lleve la matriz aumentada a una matriz escalonada reducida utilizando operaciones elementales de fila.
2. Si se produce una fila [0 0 0 ··· 0 1], el sistema es inconsistente.
3. De lo contrario, asigne las variables no principaleses (si las hay) como parámetros, y use las ecuaciones correspondientes a la matriz escalonada reducida por fila para resolver las variables principales en términos de los parámetros. ♦
Hay una variante de este procedimiento, en la que la matriz aumentada se lleva solo a la forma escalonada. Las variables no principales se asignan como parámetros como antes. Luego, la última ecuación (correspondiente a la forma escalonada) se utiliza para resolver la última variable principal en términos de los parámetros. Esta última variable principal se sustituye en todas las ecuaciones anteriores. Luego, la segunda última ecuación produce la segunda última variable principal, que también se sustituye de nuevo. El proceso continúa dando la solución general. Este procedimiento se denomina sustitución hacia atrás. Se puede demostrar que este procedimiento es numéricamente más eficiente y, por lo tanto, es importante al resolver sistemas muy grandes.
Nota: Con n ecuaciones donde n es grande, la eliminación gaussiana requiere aproximadamente n³/2 multiplicaciones y divisiones, mientras que este número es aproximadamente n³/3 si se usa la sustitución hacia atrás.
Ejemplo ilustrativo 1.2_4
Encuentre una condición en los números a, b y c de tal manera que el siguiente sistema de ecuaciones sea consistente. Cuando se cumpla esa condición, encuentre todas las soluciones (en términos de a, b y c).

Solución:
Usamos la eliminación gaussiana, excepto que ahora la matriz aumentada

tiene entradas a, b y c, así como números conocidos. El primer 1 líder está en su lugar, por lo que creamos ceros debajo de él en la columna 1:

Ha aparecido el segundo 1 líder, así que úselo para crear ceros en el resto de la columna 2:

Ahora toda la solución depende del número c − a + 2b = c − (a − 2b). La última fila corresponde a una ecuación 0 = c − (a − 2b). Si c ≠ a − 2b, no hay solución (como en el Ejemplo 1.2.2). Por lo tanto:
El sistema es consistente si y sólo si c = a − 2b.
En este caso la última matriz se convierte en
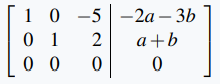
Por lo tanto, si c = a − 2b, tomar x₃ = t donde t es un parámetro da las soluciones ◊
◊
Rango
Se puede demostrar que la forma escalonada reducida de una matriz A está determinada de manera única por A. Es decir, no importa qué serie de operaciones de fila se usen para llevar A a una matriz escalonada reducida por fila, el resultado siempre será la misma matriz (Se proporciona una prueba al final de la Sección 2.5.) Por el contrario, esto no es cierto para las matrices escalonadas por filas: diferentes series de operaciones de fila pueden llevar la misma matriz A a diferentes matrices escalonadas por filas. De hecho, la matriz

se puede transformar (mediante una operación de fila) a la matriz escalonada

y luego por otra operación de fila a la matriz escalonada (reducida)

Sin embargo, sí es cierto que el número r de unos principales debe ser el mismo en cada una de estas matrices escalonadas (esto se demostrará en el Capítulo 5). Por lo tanto, el número r depende únicamente de A y no de la forma en que se lleve a A a la forma escalonada.
Definición 1.2.2 Rango de una matriz
El rango de una matriz A es el número de unos principales en cualquier matriz escalonada por filas a la cual A puede ser llevada mediante operaciones elementales de fila. ♦
Ejemplo ilustrativo 1.2_5
Calcule el rango de

Solución:
La reducción de A a la forma escalonada es

Debido a que esta matriz escalonada tiene dos 1s principales, el rango A = 2. ◊
Suponga que el rango A = r, donde A es una matriz con m filas y n columnas. Entonces r ≤ m porque los primeros 1 se encuentran en diferentes filas, y r ≤ n porque los primeros 1 se encuentran en diferentes columnas. Además, el rango tiene una aplicación útil para las ecuaciones. Recuerde que un sistema de ecuaciones lineales se llama consistente si tiene al menos una solución.
Teorema 1.2.2
|
Suponga que un sistema de m ecuaciones en n variables es consistente y que el rango de la matriz aumentada es r. 1. El conjunto de soluciones involucra exactamente n – r parámetros. |
|
Prueba. El hecho de que el rango de la matriz aumentada sea r significa que existen exactamente r variables principales y, por lo tanto, exactamente n − r variables no principales. Todas estas variables no principales se asignan como parámetros en el algoritmo gaussiano, por lo que el conjunto de soluciones involucra exactamente n – r parámetros. Por lo tanto, si r < n, hay al menos un parámetro y, por lo tanto, infinitas soluciones. Si r = n, no hay parámetros y, por lo tanto, una solución única. ◊ |
El Teorema 1.2.2 muestra que, para cualquier sistema de ecuaciones lineales, existen exactamente tres posibilidades:
1. No hay solución. Esto sucede cuando una fila [0 0 ··· 0 1] aparece en la forma escalonada. Este es el caso donde el sistema es inconsistente.
2. Solución única. Esto ocurre cuando cada variable es una variable principal.
3. Infinitas soluciones. Esto ocurre cuando el sistema es consistente y hay al menos una variable no principal, por lo que al menos un parámetro está involucrado.
Ejemplo ilustrativo 1.2_6
Suponga que la matriz A del Ejemplo 1.2.5 es la matriz aumentada de un sistema de m = 3 ecuaciones lineales en n = 3 variables. Como rango A = r = 2, el conjunto de soluciones tendrá n − r = 1 parámetros. El lector puede verificar este hecho directamente. ◊
Muchos problemas importantes involucran desigualdades lineales en lugar de ecuaciones lineales. Por ejemplo, una condición en las variables x e y podría tomar la forma de una desigualdad 2x − 5y ≤ 4 en lugar de una igualdad 2x − 5y = 4. Existe una técnica (llamada algoritmo simplex) para encontrar soluciones a un sistema de tales desigualdades que maximizan una función de la forma p = ax + by donde a y b son constantes.
⇐ (1.1. Soluciones y operaciones elementales)
(1.3. Ecuaciones homogéneas) ⇒
