| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.3 |

10.3 EL PRODUCTO PUNTO

Objetivos de aprendizaje:

10.3.1. Calcular el producto punto (producto escalar) de dos vectores dados.
10.3.2. Determinar si dos vectores dados son perpendiculares.
10.3.3. Encontrar la dirección de los cosenos de un vector dado.
10.3.4. Explicar qué se entiende por proyección vectorial de un vector sobre otro vector y describir cómo calcularlo.
10.3.5. Calcular el trabajo realizado por una fuerza dada.

       Si aplicamos una fuerza a un objeto para que el objeto se mueva, decimos que el trabajo lo realiza la fuerza. En Introducción a las aplicaciones de la integración, observamos una fuerza constante y asumimos que la fuerza se aplicaba en la dirección del movimiento del objeto. En esas condiciones, el trabajo puede expresarse como el producto de la fuerza que actúa sobre un objeto y la distancia que se mueve el objeto. En el presente capítulo, sin embargo, hemos visto que tanto la fuerza como el movimiento de un objeto pueden representarse mediante vectores.

       En esta sección, desarrollamos una operación llamada producto punto, que nos permite calcular el trabajo en el caso en que el vector de fuerza y ​​el vector de movimiento tengan direcciones diferentes. El producto punto esencialmente nos dice cuánto del vector de fuerza se aplica en la dirección del vector de movimiento. El producto punto también puede ayudarnos a medir el ángulo formado por un par de vectores y la posición de un vector en relación con los ejes de coordenadas. Incluso proporciona una prueba simple para determinar si dos vectores se encuentran en ángulo recto.

El producto punto y sus propiedades

Ya hemos aprendido cómo sumar y restar vectores. En este capítulo, investigamos dos tipos de multiplicación de vectores. El primer tipo de multiplicación vectorial se llama producto punto, según la notación que usamos para ello, y se define de la siguiente manera:

DEFINICIÓN. Producto punto

El producto escalar de los vectores \(\mathbf{u} = \langle u_1, u_2, u_3 \rangle\) y \(\mathbf{v} = \langle v_1, v_2, v_3 \rangle\) se da por la suma de los productos de las componentes:

\[ \mathbf{u} \cdot \mathbf{v} = u_1v_1 + u_2v_2 + u_3v_3. \]

♦

Note que si \(\mathbf{u}\) y \(\mathbf{v}\) son vectores bidimensionales, calculamos el producto escalar de manera similar. Por lo tanto, si \(\mathbf{u} = \langle u_1, u_2 \rangle\) y \(\mathbf{v} = \langle v_1, v_2 \rangle\), entonces

\[ \mathbf{u} \cdot \mathbf{v} = u_1v_1 + u_2v_2. \]

Cuando dos vectores se combinan bajo suma o resta, el resultado es un vector. Cuando dos vectores se combinan usando el producto punto, el resultado es un escalar. Por esta razón, al producto punto a menudo se llama producto escalar. También se le puede llamar el producto interno.

EJEMPLO ILUSTRATIVO 10.3_1. Cálculo de productos punto

1. Encuentre el producto escalar de \(\mathbf{u} = \langle 3, 5, 2 \rangle\) y \(\mathbf{v} = \langle -1, 3, 0 \rangle\).
2. Encuentre el producto escalar de \(\mathbf{p} = 10\mathbf{i} – 4\mathbf{j} + 7\mathbf{k}\) y \(\mathbf{q} = -2\mathbf{i} + \mathbf{j} + 6\mathbf{k}\).

Solución:

a.  Sustituya los componentes del vector en la fórmula del producto punto:

u ⋅ v = u₁ v₁ + u₂ v₂ + u₃ v₃ = 3 (−1) + 5 (3) + 2 (0) = − 3 + 15 + 0 = 12.

b.  El cálculo es el mismo si los vectores se escriben usando vectores unitarios estándar. Todavía tenemos tres componentes para cada vector para sustituir en la fórmula del producto escalar:

p ⋅ q = u₁ v₁ + u₂ v₂ + u₃ v₃ = 10 (−2) + (−4) (1) + (7) (6) = −20 − 4 + 42 = 18. ♦

Ejercicio de control 10.3_1

Encuentre \(\mathbf{u} \cdot \mathbf{v}\), donde \(\mathbf{u} = \langle 2, 9, -1 \rangle\) y \(\mathbf{v} = \langle -3, 1, -4 \rangle\). ♦

       Al igual que la suma y resta de vectores, el producto punto tiene varias propiedades algebraicas. Probamos algunas de estas propiedades y dejamos el resto como ejercicios.

TEOREMA 10.3.1. Propiedades del producto punto

Sean u, v y w vectores, y c sea un escalar.

i.	u · v = v · u	Propiedad conmutativa
ii.	u · (v + w) = u · v + u · w	Propiedad distributiva
iii.	c(u · v) = (cu) · v = u · (cv)	Propiedad asociativa
iv.	v · v = ‖v‖²	Propiedad de magnitud

Prueba:

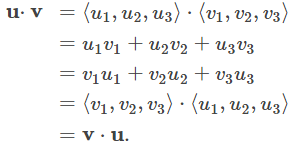
La propiedad asociativa se parece a la propiedad asociativa para la multiplicación de números reales, pero presta mucha atención a la diferencia entre los objetos escalares y vectoriales:

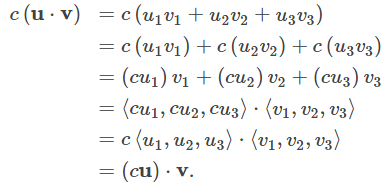
La prueba de que c (u⋅v) = u⋅ (cv) es similar.

La cuarta propiedad muestra la relación entre la magnitud de un vector y su producto punto consigo mismo:

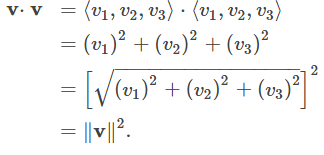
Tenga en cuenta que la definición del producto punto produce 0⋅v = 0. Por la propiedad iv., Si v⋅v = 0, entonces v = 0.

---

EJEMPLO ILUSTRATIVO 10.3_2. Uso de las  propiedades del producto punto

Sean \(\mathbf{a} = \langle 1, 2, -3 \rangle\), \(\mathbf{b} = \langle 0, 2, 4 \rangle\), y \(\mathbf{c} = \langle 5, -1, 3 \rangle\). Encuentre cada uno de los siguientes productos.

a) (a ⋅ b) c
b) a ⋅ (2c)
c) ∥b∥²

Solución:

a) Tenga presente que esta expresión pide el múltiplo escalar de c por a⋅b:

b) Esta expresión es un producto punto del vector a y el múltiplo escalar 2c:

c) Simplificar esta expresión es una aplicación directa del producto punto:

♦

Ejercicio de control 10.3_2

Encuentre los siguientes productos para \(\mathbf{p} = \langle 7, 0, 2 \rangle\), \(\mathbf{q} = \langle -2, 2, -2 \rangle\), y \(\mathbf{r} = \langle 0, 2, -3 \rangle\).

1. \((\mathbf{r} \cdot \mathbf{p}) \mathbf{q}\)
2. \(\|\mathbf{p}\|^2\)

♦

Uso del producto  punto para encontrar el ángulo entre dos vectores

Cuando dos vectores distintos de cero se colocan en posición estándar, ya sea en dos dimensiones o en tres dimensiones, forman un ángulo entre ellos (Figura 10.3_1). El producto punto proporciona una forma de encontrar la medida de este ángulo. Esta propiedad es el resultado del hecho de que podemos expresar el producto escalar en términos del coseno del ángulo formado por dos vectores.

Figura 10.3_1 Sea θ el ángulo entre dos vectores distintos de cero u y v, de modo que 0 ≤ θ ≤ π.

TEOREMA 10.3.2. Evaluación de un producto punto

El producto punto de dos vectores es el producto de la magnitud de cada vector y el coseno del ángulo entre ellos:

u⋅v = ∥u∥∥v∥cosθ. ♦

---

Prueba:

Coloque los vectores u y v en la posición estándar y considere el vector v − u (Figura 10.3_2). Estos tres vectores forman un triángulo con longitudes laterales ∥u∥, ∥v∥ y ∥v − u∥.

(Figura 10.3_2 Las longitudes de los lados del triángulo están dadas por las magnitudes de los vectores que forman el triángulo.)

Recuerde de la trigonometría que la ley de los cosenos describe la relación entre las longitudes laterales del triángulo y el ángulo θ. La aplicación de la ley de cosenos aquí da

El producto punto proporciona una forma de reescribir el lado izquierdo de esta ecuación:

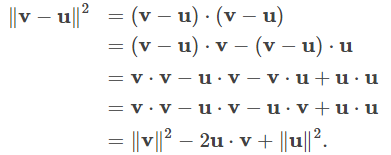
Sustituyendo en la ley del coseno para vectores, se tiene:

---

       Podemos usar esta forma del producto punto para encontrar la medida del ángulo entre dos vectores distintos de cero. La siguiente ecuación reorganiza la ecuación dada en el Teorema 10.3.2 para resolver el coseno del ángulo:

Usando esta ecuación, podemos encontrar el coseno del ángulo entre dos vectores distintos de cero. Como estamos considerando el ángulo más pequeño entre los vectores, suponemos 0° ≤ θ ≤ 180° (o 0 ≤ θ ≤ π si estamos trabajando en radianes). El coseno inverso es único en este rango, por lo que podemos determinar la medida del ángulo θ.

EJEMPLO ILUSTRATIVO 10.3_2. Encontrar el ángulo entre dos vectores

Encuentre la medida del ángulo entre cada par de vectores.

1. \(\mathbf{i} + \mathbf{j} + \mathbf{k}\) y \(2\mathbf{i} – \mathbf{j} – 3\mathbf{k}\)
2. \(\langle 2, 5, 6 \rangle\) y \(\langle -2, -4, 4 \rangle\)

Solución:

a) Para encontrar el coseno del ángulo formado por los dos vectores, sustituya las componentes de los vectores en la ecuación:

Por lo tanto,

b) Comience por encontrar el valor del coseno del ángulo entre los vectores:

Ahora, cosθ = 0 y 0 ≤ θ ≤ π, entonces θ = π / 2. ♦

Ejercicio de control 10.3_3

Encuentre la medida del ángulo, en radianes, formado por los vectores \(\mathbf{a} = \langle 1, 2, 0 \rangle\) y \(\mathbf{b} = \langle 2, 4, 1 \rangle\). Redondee a la centésima más cercana. ♦

Vectores ortogonales

       El ángulo entre dos vectores puede ser agudo (0 < cosθ  < 1), obtuso (−1 < cosθ < 0) o recto (cosθ = −1). Si cosθ = 1, ambos vectores tienen la misma dirección. Si cosθ = 0, entonces los vectores, cuando se colocan en posición estándar, forman un ángulo recto (Figura 10.3_3). Podemos formalizar este resultado en un teorema con respecto a los vectores ortogonales (perpendiculares).

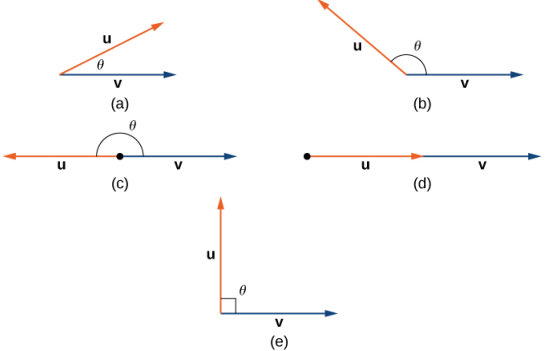
Figura 10.3_3 (a) Un ángulo agudo tiene 0 < cosθ < 1. (b) Un ángulo obtuso tiene −1 < cosθ < 0. (c) Una línea recta tiene cosθ = −1. (d) Si los vectores tienen la misma dirección, cosθ = 1. (e) Si los vectores son ortogonales (perpendiculares), cosθ = 0.

TEOREMA 10.3.3. Vectores ortogonales

Los vectores distintos de cero u y v son vectores ortogonales si y sólo si

u ⋅ v = 0.  ♦

---

Prueba

Supongamos que u y v son vectores distintos de cero y que θ denota el ángulo entre ellos. Primero, suponga que u⋅v = 0. Luego

∥u∥∥v∥cosθ = 0.

Sin embargo, ∥u∥ ≠ 0 y ∥v∥ ≠ 0, por lo que debemos tener cosθ = 0. Por lo tanto, θ = 90 °, y los vectores son ortogonales.

Ahora suponga que u y v son ortogonales. Entonces θ = 90 ° y tenemos

u⋅v = ∥u∥∥v∥cosθ = ∥u∥∥v∥cos90° = ∥u∥∥v∥ (0) = 0.

---

       Los términos ortogonal, perpendicular y normal indican que los objetos matemáticos se cortan en ángulo recto. El uso de cada término está determinado principalmente por su contexto. Decimos que los vectores son ortogonales y las rectas son perpendiculares. El término normal se usa con mayor frecuencia cuando se mide el ángulo hecho con un plano u otra superficie.

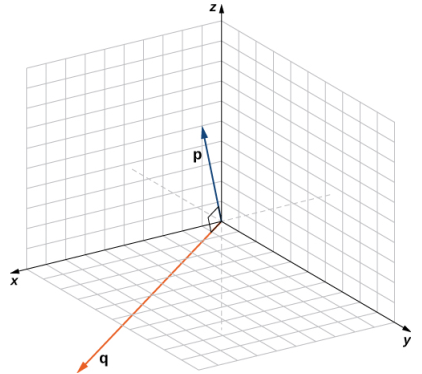
EJEMPLO ILUSTRATIVO 10.3_3. Identificación de vectores ortogonales

Determine si \(\mathbf{p} = \langle 1, 0, 5 \rangle\) y \(\mathbf{q} = \langle 10, 3, -2 \rangle\) son vectores ortogonales.

Solución:

Usando la definición, solo necesitamos verificar el producto punto de los vectores:

p⋅q = 1 (10) + (0) (3) + (5) (- 2) = 10 + 0 − 10 = 0.

Como p⋅q = 0, los vectores son ortogonales (figura 10.3_4).

Ejercicio de control 10.3_4

¿Para qué valor de \(x\) es \(\mathbf{p} = \langle 2, 8, -1 \rangle\) ortogonal a \(\mathbf{q} = \langle x, -1, 2 \rangle\)? ♦

EJEMPLO ILUSTRATIVO 10.3_4. Medición del ángulo formado por dos vectores

Sean \(\mathbf{v} = \langle 2, 3, 3 \rangle\). Encuentre las medidas de los ángulos formados por los siguientes vectores.

a) v e i
b) v y j
c) v y k

Solución:
a) Sea α el ángulo formado por v e i:

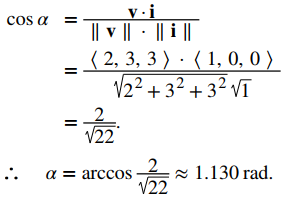
b) Supongamos que β representa el ángulo formado por v y j:

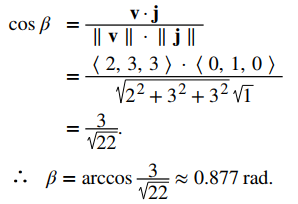
c) Deje γ representar el ángulo formado por v y k:

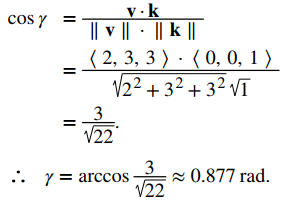
Ejercicio de control 10.3_5

Sean \(\mathbf{v} = \langle 3, -5, 1 \rangle\). Encuentre la medida de los ángulos formados por cada par de vectores.

1. \(\mathbf{v}\) e \(\mathbf{i}\)
2. \(\mathbf{v}\) y \(\mathbf{j}\)
3. \(\mathbf{v}\) y \(\mathbf{k}\)

       El ángulo que forma un vector con cada uno de los ejes de coordenadas, llamado ángulo de dirección, es muy importante en los cálculos prácticos, especialmente en un campo como la ingeniería. Por ejemplo, en ingeniería astronáutica, el ángulo en el que se lanza un cohete debe determinarse con mucha precisión. Un error muy pequeño en el ángulo puede hacer que el cohete se desplace cientos de millas. Los ángulos de dirección a menudo se calculan utilizando el producto escalar y los cosenos de los ángulos, llamados cosenos de dirección. Por lo tanto, definimos ambos ángulos y sus cosenos.

Definición. Ángulos y cosenos de dirección

Los ángulos formados por un vector distinto de cero y los ejes de coordenadas se denominan ángulos de dirección para el vector (Figura 10.3_5). Los cosenos para estos ángulos se denominan cosenos de dirección. ♦

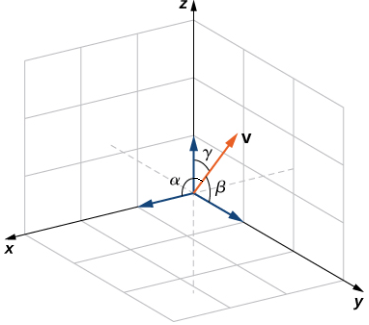
Figura 10.3_5 El ángulo α está formado por el vector v y el vector unitario i. El ángulo β está formado por el vector v y el vector unitario j. El ángulo γ está formado por el vector v y el vector unitario k.

En el Ejemplo 10.3.4, los cosenos directores de \(\mathbf{v} = \langle 2, 3, 3 \rangle\) son \(\cos \alpha = \frac{2}{\sqrt{22}}\), \(\cos \beta = \frac{3}{\sqrt{22}}\) y \(\cos \gamma = \frac{3}{\sqrt{22}}\). Los ángulos directores de \(\mathbf{v}\) son \(\alpha = 1.130\) rad, \(\beta = 0.877\) rad, y \(\gamma = 0.877\) rad.

       Hasta ahora, nos hemos centrado principalmente en vectores relacionados con la fuerza, el movimiento y la posición en el espacio físico tridimensional. Sin embargo, los vectores a menudo se usan de formas más abstractas. Por ejemplo, supongamos que un vendedor de frutas vende manzanas, plátanos y naranjas. En un día determinado, vende 30 manzanas, 12 plátanos y 18 naranjas. Podría usar un vector de cantidad, 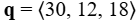, para representar la cantidad de fruta que vendió ese día. De manera similar, podría usar un vector de precios, 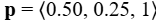, para indicar que vende sus manzanas por 50¢ cada una, plátanos por 25¢ cada uno y naranjas por $1 cada una. En este ejemplo, aunque todavía podríamos graficar estos vectores, no los interpretamos como representaciones literales de posición en el mundo físico. Simplemente estamos usando vectores para realizar un seguimiento de piezas particulares de información sobre manzanas, plátanos y naranjas.

Esta idea puede parecer un poco extraña, pero si simplemente consideramos los vectores como una forma de ordenar y almacenar datos, descubriremos que pueden ser una herramienta bastante poderosa. Volviendo al vendedor de frutas, pensemos en el producto escalar, q ⋅ p. Lo calculamos multiplicando la cantidad de manzanas vendidas (30) por el precio por manzana (50¢), la cantidad de bananas vendidas por el precio de la banana y la cantidad de naranjas vendidas por el precio de la naranja. Luego sumamos todos estos valores. Entonces, en este ejemplo, el producto punto nos dice cuánto dinero tenía el vendedor de frutas en ventas ese día en particular.

Cuando usamos vectores de esta manera más general, no hay razón para limitar el número de componentes a tres. ¿Qué pasa si el vendedor de fruta decide comenzar a vender toronja? En ese caso, le gustaría usar vectores de cantidad y precio de cuatro dimensiones para representar la cantidad de manzanas, plátanos, naranjas y toronjas vendidas, y sus precios unitarios. Como es de esperar, para calcular el producto escalar de los vectores de cuatro dimensiones, simplemente agregamos los productos de los componentes como antes, pero la suma tiene cuatro términos en lugar de tres.

EJEMPLO ILUSTRATIVO 10.3_5. Usando vectores en un contexto económico

Solución:

Los vectores de costo, precio de venta y cantidad son

Las ventas de AAA para el mes de mayo se pueden calcular utilizando el producto punto p⋅q. Tenemos

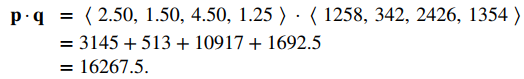
Entonces, AAA recibió $ 16,267.50 durante el mes de mayo.

Para calcular la ganancia, primero debemos calcular cuánto pagó AAA por los artículos vendidos. Usamos el producto punto c⋅q para obtener

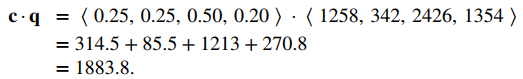
Entonces, AAA pagó $ 1,883.80 por los artículos que vendieron. Su beneficio, entonces, está dado por

Por lo tanto, AAA Party Supply Store ganó $ 14.383,70 en mayo. ♦

Ejercicio de control 10.3_6

El 1 de junio, la tienda de artículos para fiestas AAA decidió aumentar el precio que cobra por los recuerdos para fiestas a $2 por paquete. También cambiaron de proveedor para sus invitaciones, y ahora pueden comprar invitaciones por solo 10¢ por paquete. Todos sus otros costos y precios permanecen iguales. Si AAA vende 1408 invitaciones, 147 recuerdos para fiestas, 2112 decoraciones y 1894 artículos de servicio de alimentos en el mes de junio, use vectores y productos punto para calcular sus ventas totales y ganancias para junio. ♦

Proyecciones vectoriales

Como hemos visto, la suma combina dos vectores para crear un vector resultante. Pero, ¿qué pasa si se nos da un vector y necesitamos encontrar sus partes componentes? Utilizamos proyecciones vectoriales para realizar el proceso opuesto; pueden descomponer un vector en sus componentes. La magnitud de una proyección vectorial es una proyección escalar. Por ejemplo, si un niño tira del mango de un vagón en un ángulo de 55 °, podemos usar proyecciones para determinar cuánta fuerza sobre el mango está moviendo el vagón hacia adelante (Figura 10.3_5). Volvemos a este ejemplo y aprendemos cómo resolverlo después de ver cómo calcular las proyecciones.

Figura 10.3_6 Cuando un niño tira de una carreta, solo el componente horizontal de la fuerza impulsa la carreta hacia adelante.

Definición. Proyección vectorial

La proyección vectorial de \(\mathbf{v}\) sobre \(\mathbf{u}\) es el vector marcado \(\text{proj}_{\mathbf{u}} \mathbf{v}\) en la figura 10.3_7. Tiene el mismo punto inicial que \(\mathbf{u}\) y \(\mathbf{v}\) y la misma dirección que \(\mathbf{u}\), y representa el componente de \(\mathbf{v}\) que actúa en la dirección de \(\mathbf{u}\). Si \(\theta\) representa el ángulo entre \(\mathbf{u}\) y \(\mathbf{v}\), entonces, por las propiedades de los triángulos, sabemos que la longitud de \(\text{proj}_{\mathbf{u}} \mathbf{v}\) es \(\|\text{proj}_{\mathbf{u}} \mathbf{v}\| = \|\mathbf{v}\| |\cos \theta|\). Al expresar \(\cos \theta\) en términos del producto escalar, esto se convierte en

\[ \begin{aligned} \|\text{proj}_{\mathbf{u}} \mathbf{v}\| &= \|\mathbf{v}\| |\cos \theta| \\ &= \|\mathbf{v}\| \left| \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\| \|\mathbf{v}\|} \right| \\ &= \frac{|\mathbf{u} \cdot \mathbf{v}|}{\|\mathbf{u}\|}. \end{aligned} \]

Ahora multiplicamos por un vector unitario en la dirección de \(\mathbf{u}\) para obtener \(\text{proj}_{\mathbf{u}} \mathbf{v}\):

\[ \text{proj}_{\mathbf{u}} \mathbf{v} = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\|} \left( \frac{1}{\|\mathbf{u}\|} \mathbf{u} \right) = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\|^2} \mathbf{u}. \]

La longitud de este vector también se conoce como la proyección escalar de \(\mathbf{v}\) sobre \(\mathbf{u}\) y se denota por

\[ \|\text{proj}_{\mathbf{u}} \mathbf{v}\| = \text{comp}_{\mathbf{u}} \mathbf{v} = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\|}. \]

Figura 10.3_7 La proyección de v sobre u muestra el componente del vector v en la dirección de u.

EJEMPLO ILUSTRATIVO 10.3_6. Encontrar proyecciones

Encuentre la proyección de v sobre u.
 
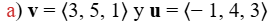
  b) v = 3i − 2j y u = i + 6j

Solución:

a) Sustituya los componentes de v y u en la fórmula para la proyección:

b) Para encontrar la proyección bidimensional, simplemente adapte la fórmula al caso bidimensional:

♦

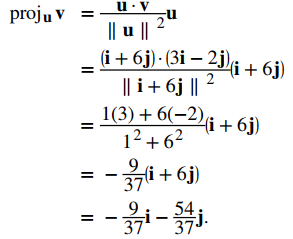
A veces es útil descomponer vectores; es decir, dividir un vector en una suma. Este proceso se llama la resolución de un vector en componentes. Las proyecciones nos permiten identificar dos vectores ortogonales que tienen una suma deseada. Por ejemplo, sean \(\mathbf{v} = \langle 6, -4 \rangle\) y \(\mathbf{u} = \langle 3, 1 \rangle\). Queremos descomponer el vector \(\mathbf{v}\) en componentes ortogonales tal que uno de los vectores componentes tenga la misma dirección que \(\mathbf{u}\).

Primero encontramos el componente que tiene la misma dirección que u proyectando v sobre u. Deje p = projᵤv. Entonces tenemos

Ahora considere el vector q = v − p. Tenemos

Claramente, por la forma en que definimos q, tenemos v = q + p, y

Por lo tanto, q y p son ortogonales.

EJEMPLO ILUSTRATIVO 10.3_7. Resolviendo vectores en componentes

Exprese \(\mathbf{v} = \langle 8, -3, -5 \rangle\) como una suma de vectores ortogonales tal que uno de los vectores tenga la misma dirección que \(\mathbf{u} = \langle 2, 3, 2 \rangle\).

Solución:
Supongamos que p representa la proyección de v sobre u:

Entonces,

Para verificar nuestro trabajo, podemos usar el producto punto para verificar que p y q son vectores ortogonales:

Luego,

♦

Ejercicio de control 10.3_7

Exprese \(\mathbf{v} = 5\mathbf{i} – \mathbf{j}\) como una suma de vectores ortogonales tal que uno de los vectores tenga la misma dirección que \(\mathbf{u} = 4\mathbf{i} + 2\mathbf{j}\). ♦

EJEMPLO ILUSTRATIVO 10.3_8. Proyección Escalar de Velocidad

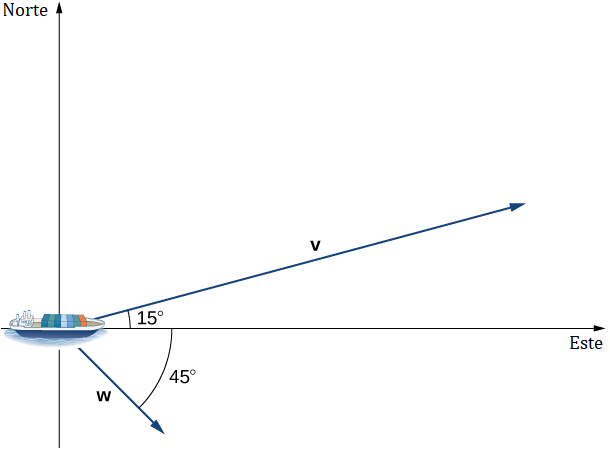
Un barco de contenedores sale del puerto y viaja 15° al norte del este. Su motor genera una velocidad de 20 nudos a lo largo de ese camino (ver la siguiente figura). Además, la corriente oceánica mueve el barco hacia el noreste a una velocidad de 2 nudos. Considerando tanto el motor como la corriente, ¿qué tan rápido se mueve el barco en la dirección 15° al norte del este? Redondea la respuesta a dos decimales.

Solución:

Sea v el vector de velocidad generado por el motor, y sea w el vector de velocidad de la corriente. Ya sabemos ∥v∥ = 20 a lo largo de la ruta deseada. Solo necesitamos agregar la proyección escalar de w en v. Obtenemos

El barco se mueve a 21.73 nudos en la dirección 15° al norte del este. ♦

Ejercicio de control 10.3_8

Repita el ejemplo anterior, pero asuma que la corriente oceánica se mueve hacia el sureste en lugar del noreste, como se muestra en la siguiente figura.

♦

Trabajo

Ahora que entendemos los productos punto, podemos ver cómo aplicarlos a situaciones de la vida real. La aplicación más común del producto escalar de dos vectores está en el cálculo del trabajo.

Por física, sabemos que el trabajo se realiza cuando un objeto es movido por una fuerza. Cuando la fuerza es constante y se aplica en la misma dirección en que se mueve el objeto, definimos el trabajo realizado como el producto de la fuerza y la distancia que recorre el objeto: W = Fd. Vimos varios ejemplos de este tipo en capítulos anteriores. Ahora imagine que la dirección de la fuerza es diferente de la dirección del movimiento, como en el ejemplo de un niño que tira de un carro. Para encontrar el trabajo realizado, necesitamos multiplicar el componente de la fuerza que actúa en la dirección del movimiento por la magnitud del desplazamiento. El producto punto nos permite hacer precisamente eso. Si representamos una fuerza aplicada por un vector F y el desplazamiento de un objeto por un vector s, entonces el trabajo realizado por la fuerza es el producto escalar de F y s.

Definición. Trabajo

Cuando una fuerza constante se aplica a un objeto de modo que el objeto se mueve en línea recta desde el punto \(P\) al punto \(Q\), el trabajo \(W\) realizado por la fuerza \(\mathbf{F}\), actuando a un ángulo \(\theta\) desde la línea de movimiento, está dado por

\[ W = \mathbf{F} \cdot \overrightarrow{PQ} = \|\mathbf{F}\| \|\overrightarrow{PQ}\| \cos \theta. \]

♦

Volvamos al problema del carro del niño presentado anteriormente. Supongamos que un niño tira de un carro con una fuerza que tiene una magnitud de 8 lb sobre el mango en un ángulo de 55°. Si el niño tira de la carreta 50 pies, encuentre el trabajo realizado por la fuerza (Figura 10.3_8).

Figura 10.3_8 El componente horizontal de la fuerza es la proyección de F sobre el eje x positivo.

Nosotros tenemos

En unidades estándar de EE. UU., Medimos la magnitud de la fuerza ∥F∥ en libras. La magnitud del vector de desplazamiento.

nos dice qué tan lejos se movió el objeto, y se mide en pies. La unidad de medida habitual para el trabajo, entonces, es la libra-pie. Una libra de pie es la cantidad de trabajo requerida para mover un objeto que pesa 1 libra a una distancia de 1 pie hacia arriba. En el sistema métrico, la unidad de medida de la fuerza es el newton (N), y la unidad de medida de magnitud para el trabajo es un newton-metro (N · m), o un julio (J).

EJEMPLO ILUSTRATIVO 10.3_9. Cálculo de Trabajo 

Una cinta transportadora genera una fuerza F = 5i − 3j + k que mueve una maleta desde el punto (1, 1, 1) al punto (9, 4,7 ) a lo largo de una línea recta. Encuentra el trabajo realizado por la cinta transportadora. La distancia se mide en metros y la fuerza se mide en newtons.

Solución:

Ejercicio de control 10.3_9

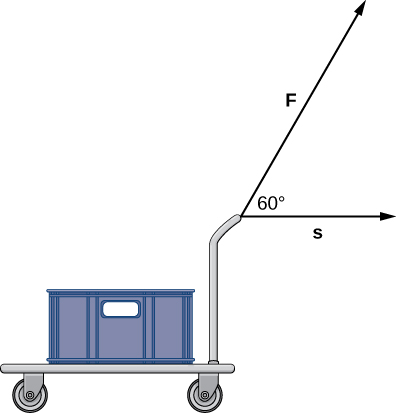
Se aplica una fuerza constante de 30 lb en un ángulo de 60° para tirar de un carrito de mano 10 pies a través del suelo (Figura 10.3.9). ¿Cuál es el trabajo realizado por esta fuerza?

Figura 10.3.9