| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.5 |
10.5 ECUACIONES DE RECTAS Y PLANOS EN EL ESPACIO: Objetivos de aprendizaje
10.5.1. Escriba el vector, paramétrico y simétrico de una recta a través de un punto dado en una dirección dada, y una recta a través de dos puntos dados.
10.5.2. Encuentra la distancia desde un punto a una recta dada.
10.5.3. Escribe las ecuaciones vectoriales y escalares de un plano a través de un punto dado con una normal dada.
10.5.4. Encuentra la distancia desde un punto a un plano dado.
10.5.5. Encuentra el ángulo entre dos planos.
Por ahora, estamos familiarizados con la escritura de ecuaciones que describen una recta en dos dimensiones. Para escribir una ecuación para una recta, debemos conocer dos puntos en la recta, o debemos conocer la dirección de la recta y al menos un punto a través del cual pasa la recta. En dos dimensiones, usamos el concepto de pendiente para describir la orientación o dirección de una recta. En tres dimensiones, describimos la dirección de una recta usando un vector paralelo a la recta. En esta sección, examinamos cómo usar ecuaciones para describir rectas y planos en el espacio.
Ecuaciones para una recta en el espacio
Primero exploremos lo que significa que dos vectores sean paralelos. Recuerde que los vectores paralelos deben tener la misma dirección o direcciones opuestas. Si dos vectores distintos de cero, u y v, son paralelos, afirmamos que debe haber un escalar, k, tal que u = kv. Si u y v tienen la misma dirección, simplemente elija k = ∥u∥/ ∥v∥. Si u y v tienen direcciones opuestas, elija k = −∥u∥/∥v∥. Tenga en cuenta que lo contrario se mantiene también. Si u = kv para algún escalar k, entonces u y v tienen la misma dirección (k > 0) o direcciones opuestas (k < 0), entonces u y v son paralelos. Por lo tanto, dos vectores distintos de cero u y v son paralelos si y solo si u = kv para algún escalar k. Por convención, el vector cero 0 se considera paralelo a todos los vectores.
Como en dos dimensiones, podemos describir una recta en el espacio usando un punto en la recta y la dirección de la recta, o un vector paralelo, que llamamos el vector de dirección (Figura 10.5_1). Sea L una recta en el espacio que pasa por el punto P (x0, y0, z0). Sea v = ⟨a, b, c⟩ un vector paralelo a L. Entonces,

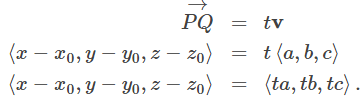
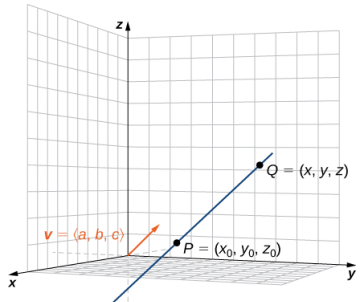
Usando operaciones vectoriales, podemos reescribir la ecuación anterior como

Configurando r = ⟨x, y, z⟩ y r0 = ⟨x0, y0, z0⟩, ahora tenemos la ecuación vectorial de una recta:
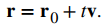
La ecuación de componentes,
La ecuación de componentes,
![]()
muestra que las siguientes ecuaciones son simultáneamente verdaderas:
x − x0 = ta,
y − y0 = tb y
z − z0 = tc.
Si resolvemos cada una de estas ecuaciones para las variables componentes x, y, y z, obtenemos un conjunto de ecuaciones en las que cada variable se define en términos del parámetro t y que, juntas, describen la recta. Este conjunto de tres ecuaciones forma un conjunto de ecuaciones paramétricas de una recta:
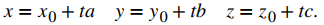
Si resolvemos cada una de las ecuaciones para t asumiendo que a, b y c no son cero, obtenemos una descripción diferente de la misma recta:
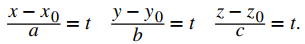
Como cada expresión es igual a t, todas tienen el mismo valor. Podemos establecerlos iguales entre sí para crear ecuaciones simétricas de una recta:
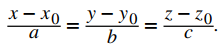
Resumimos los resultados anteriores en el siguiente teorema.
TEOREMA 10.5_1. Ecuaciones paramétricas y simétricas de una recta
Una recta $L$ paralela al vector $\mathbf{v} = \langle a, b, c \rangle$ y que pasa por el punto $P(x_0, y_0, z_0)$ puede describirse mediante las siguientes ecuaciones paramétricas:
$$x = x_0 + ta, \quad y = y_0 + tb, \quad \text{y} \quad z = z_0 + tc.$$
Si las constantes $a, b$ y $c$ son todas distintas de cero, entonces $L$ puede describirse mediante la ecuación simétrica de la recta:
$$\frac{x – x_0}{a} = \frac{y – y_0}{b} = \frac{z – z_0}{c}.$$
Las ecuaciones paramétricas de una recta no son únicas. El uso de un vector paralelo diferente o un punto diferente en la recta conduce a una representación equivalente diferente. Cada conjunto de ecuaciones paramétricas conduce a un conjunto relacionado de ecuaciones simétricas, por lo que se deduce que una ecuación simétrica de una recta tampoco es única.
EJEMPLO ILUSTRATIVO 10.5_1. Ecuaciones de una recta en el espacio
Encuentre ecuaciones paramétricas y simétricas de la recta que pasa por los puntos (1, 4, −2) y (−3, 5, 0).
Solución:
Primero, identifique un vector paralelo a la recta:
v = ⟨− 3 − 1, 5 − 4, 0 − (−2)⟩ = ⟨− 4, 1, 2⟩.
Use cualquiera de los puntos dados en la recta para completar las ecuaciones paramétricas:
x = 1− 4t, y = 4 + t, y z = −2 + 2t.
Resuelve cada ecuación para t para crear la ecuación simétrica de la recta:
(x − 1)/(−4) = y − 4 = (z + 2)/2. ♦
Ejercicio de control 10.5.1
Encuentra ecuaciones paramétricas y simétricas de la recta que pasa por puntos (1, −3, 2) y (5, −2, 8). ♦
A veces no queremos la ecuación de una recta completa, solo un segmento de recta. En este caso, limitamos los valores de nuestro parámetro t. Por ejemplo, sean P (x0, y0, z0) y Q (x1, y1, z1) puntos en una recta, y sean p = ⟨x0, y0, z0⟩ y q = ⟨x1, y1, z1⟩ vectores de posición asociados. Además, sea r = ⟨x, y, z⟩. Queremos encontrar una ecuación vectorial para el segmento de recta entre P y Q. Usando P como nuestro punto conocido en la recta, y

como la ecuación del vector de dirección, la ecuación vectorial de una recta (r = r0 + t v) da:

Usando propiedades de vectores, entonces

Por lo tanto, la ecuación vectorial de la recta que pasa por P y Q es

Recuerde que no queríamos la ecuación de la recta completa, solo el segmento de recta entre P y Q. Observe que cuando t = 0, tenemos r = p, y cuando t = 1, tenemos r = q. Por lo tanto, la ecuación vectorial del segmento de recta entre P y Q es
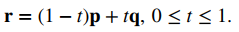
Volviendo a la ecuación vectorial de una recta (r = r0 + t v), también podemos encontrar ecuaciones paramétricas para este segmento de recta. Tenemos

Entonces, las ecuaciones paramétricas son
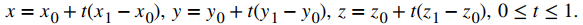
EJEMPLO ILUSTRATIVO 10.5_2. Ecuaciones paramétricas de un segmento de recta
Halle ecuaciones paramétricas del segmento de recta entre los puntos P (2, 1, 4) y Q (3, −1, 3).
Solución:
Por la ecuación paramétrica anterior, tenemos

Trabajando con cada componente por separado, obtenemos
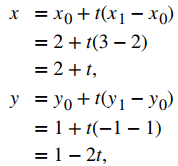
y

Por lo tanto, las ecuaciones paramétricas para el segmento de recta son
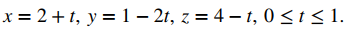
Ejercicio de control 10.5.2
Encontrar ecuaciones paramétricas del segmento de línea entre puntos 𝑃(−1, 3, 6) y 𝑄(−8, 2, 4). ♦
Distancia entre un punto y una recta
Ya sabemos cómo calcular la distancia entre dos puntos en el espacio. Ahora ampliamos esta definición para describir la distancia entre un punto y una recta en el espacio. Existen varios contextos del mundo real cuando es importante poder calcular estas distancias. Al construir una casa, por ejemplo, los constructores deben considerar los requisitos de “retroceso”, cuando las estructuras o los accesorios deben estar a una cierta distancia de la línea de la propiedad. Los viajes aéreos ofrecen otro ejemplo. Las aerolíneas están preocupadas por las distancias entre las áreas pobladas y las rutas de vuelo propuestas.
Sea L una recta en el plano y sea M cualquier punto que no esté en la recta. Luego, definimos la distancia d de M a L como la longitud del segmento de recta MP, donde P es un punto en L tal que MP es perpendicular a L (Figura 10.5_1).
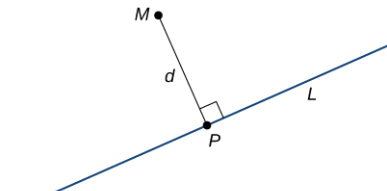
Figura 10.5_1 La distancia desde el punto M hasta la recta L es la longitud del segmento MP.
Cuando buscamos la distancia entre una recta y un punto en el espacio, también se aplica la figura 10.5_1. Todavía definimos la distancia como la longitud del segmento de recta perpendicular que conecta el punto con la recta. En el espacio, sin embargo, no hay una manera clara de saber qué punto de la recta crea un segmento de recta tan perpendicular, por lo que seleccionamos un punto arbitrario en la recta y utilizamos las propiedades de los vectores para calcular la distancia. Por lo tanto, sea P un punto arbitrario en la línea L y sea v un vector de dirección para L (Figura 10.5_2).
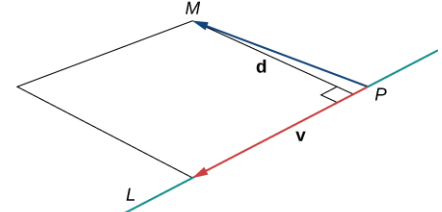
De acuerdo con el área de un paralelogramo, los vectores
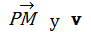
forman dos lados de un paralelogramo con área
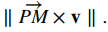
Usando una fórmula de geometría, el área de este paralelogramo también se puede calcular como el producto de su base y altura:
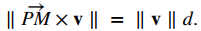
Podemos usar esta fórmula para encontrar una fórmula general para la distancia entre una recta en el espacio y cualquier punto que no esté en la recta.
TEOREMA 10.5_2. Distancia de un punto a una recta
Sea $L$ una recta en el espacio que pasa por el punto $P$ con vector director $\mathbf{v}$. Si $M$ es cualquier punto que no está en $L$, entonces la distancia de $M$ a $L$ es:
$$d = \frac{\| \overrightarrow{PM} \times \mathbf{v} \|}{\| \mathbf{v} \|}.$$
EJEMPLO ILUSTRATIVO 10.5_3. Calcular la distancia de un punto a una recta
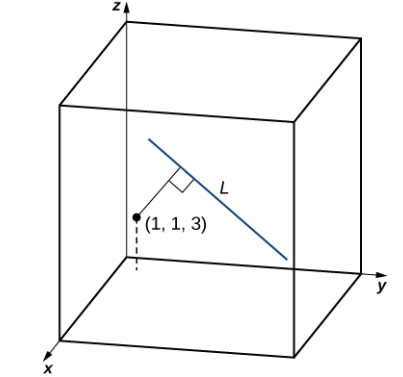
Encuentre la distancia entre el punto M = (1, 1, 3) y la recta (x − 3)/4 = (y + 1)/2 = z − 3.
Solución:
A partir de las ecuaciones simétricas de la recta, sabemos que el vector v = ⟨4, 2, 1⟩ es un vector de dirección para la recta. Al establecer las ecuaciones simétricas de la rect igual a cero, vemos que el punto P (3, -1, 3) se encuentra en la recta. Luego,
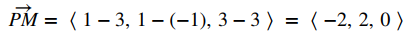
Para calcular la distancia, necesitamos encontrar
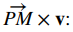

Por lo tanto, la distancia entre el punto y la recta es (Figura 10.5_3)

Ejercicio de control 10.5.3
Encuentra la distancia entre puntos (0, 3, 6) y la recta con ecuaciones paramétricas 𝑥 = 1 − 𝑡, 𝑦 = 1 + 2𝑡, 𝑧 = 5 + 3𝑡. ♦
Relaciones entre rectas
Dadas dos rectas en el plano bidimensional, las rectas son coincidentes, son paralelas pero no coincidentes, o se intersectan en un solo punto. En tres dimensiones, es posible un cuarto caso. Si dos rectas en el espacio no son paralelas, pero no se cruzan, entonces se dice que las rectas son rectas oblicuas (Figura 10.5_4).
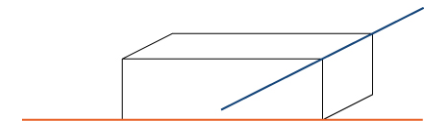
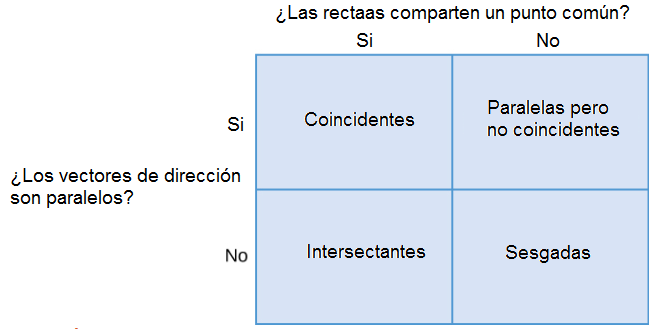
Para clasificar las rectas como paralelas pero no coincidentes, coincidentes, intersecantes o sesgadas, necesitamos saber dos cosas: si los vectores de dirección son paralelos y si las rectas comparten un punto (Figura 10.5_5).
EJEMPLO ILUSTRATIVO 10.5_4. Clasificación de rectas en el espacio
Para cada par de rectas, determine si las rectas son coincidentes, paralelas pero no coincidentes, sesgadas o interceptadas.
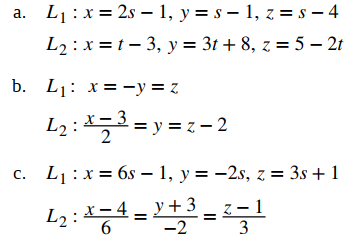
Solución:
a. La recta L1 tiene el vector de dirección v1 = ⟨2, 1, 1⟩; la recta L2 tiene el vector de dirección v2 = ⟨1, 3, −2⟩. Debido a que los vectores de dirección no son vectores paralelos, las rectas se intersecan o se sesgan. Para determinar si las rectas se cruzan, vemos si hay un punto, (x, y, z), que se encuentra en ambas rectas. Para encontrar este punto, usamos las ecuaciones paramétricas para crear un sistema de ecuaciones:
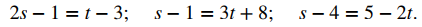
Por la primera ecuación, t = 2s + 2. Sustituyendo en la segunda ecuación se obtiene
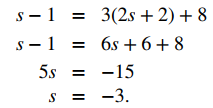
La sustitución en la tercera ecuación, sin embargo, produce una contradicción:
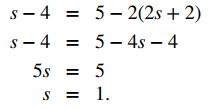
No existe un punto único que satisfaga las ecuaciones paramétricas para L1 y L2 simultáneamente. Estas rectas no se intersectan, por lo que son asimétricas (consulte la siguiente figura).

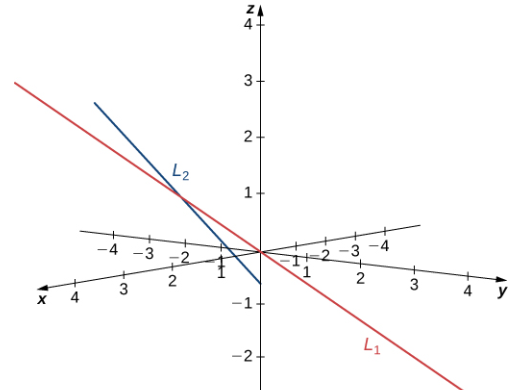
b. La recta L1 tiene el vector de dirección v1 = ⟨1, −1, 1⟩ y pasa a través del origen, (0, 0, 0). La recta L2 tiene un vector de dirección diferente, v2 = ⟨2, 1, 1⟩, por lo que estas rectas no son paralelas o coincidentes. Supongamos que r representa el parámetro para la recta L1 y que s representa el parámetro para L2:
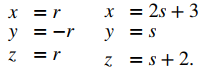
Resuelve el sistema de ecuaciones para encontrar r = 1 y s = −1. Si necesitamos encontrar el punto de intersección, podemos sustituir estos parámetros en las ecuaciones originales para obtener (1, −1, 1) (ver la siguiente figura).
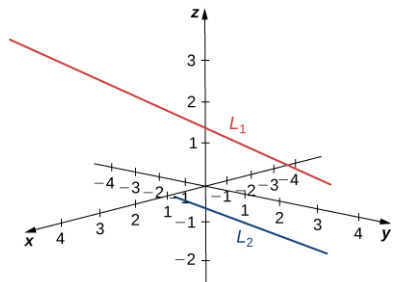
c. Las rectas L1 y L2 tienen vectores de dirección equivalentes: v = ⟨6, −2, 3⟩. Estas dos rectas son paralelas (ver la siguiente figura).
Ejercicio de control 10.5.4
Describa la relación entre las rectas con las siguientes ecuaciones paramétricas:
$$x = 1 – 4t, \quad y = 3 + t, \quad z = 8 – 6t$$ $$x = 2 + 3s, \quad y = 2s, \quad z = -1 – 3s$$
Ecuaciones para un plano
Sabemos que una recta está determinada por dos puntos. En otras palabras, para dos puntos distintos, hay exactamente una recta que pasa a través de esos puntos, ya sea en dos dimensiones o en tres. Del mismo modo, dados tres puntos que no todos se encuentran en la misma recta, hay un plano único que pasa por estos puntos. Así como una recta está determinada por dos puntos, un plano está determinado por tres.
Esta puede ser la forma más sencilla de caracterizar un plano, pero también podemos usar otras descripciones. Por ejemplo, dadas dos rectas distintas que se intersecan, hay exactamente un plano que contiene ambas rectas. Un plano también está determinado por una recta y cualquier punto que no se encuentre en la recta. Estas caracterizaciones surgen naturalmente de la idea de que un plano está determinado por tres puntos. Quizás la caracterización más sorprendente de un plano es en realidad la más útil.
Imagine un par de vectores ortogonales que comparten un punto inicial. Visualice agarrando uno de los vectores y girándolo. A medida que gira, el otro vector gira y barre un plano. Aquí, describimos ese concepto matemáticamente. Sea n = ⟨a, b, c⟩ un vector y P = (x0, y0, z0) un punto. Entonces el conjunto de todos los puntos Q = (x, y, z) tal que el vector PQ es ortogonal a n forma un plano (figura 10.5_6). Decimos que n es un vector normal, o perpendicular al plano. Recuerde, el producto escalar de los vectores ortogonales es cero. Este hecho genera la ecuación vectorial de un plano: n⋅PQ = 0. Reescribir esta ecuación proporciona formas adicionales de describir el plano:
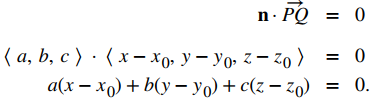
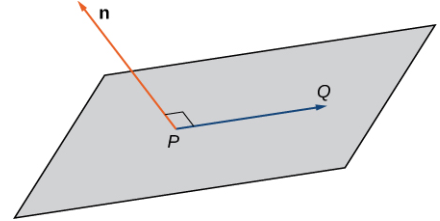
Definición. Ecuación de un plano
Dado un punto $P$ y un vector $\mathbf{n}$, el conjunto de todos los puntos $Q$ que satisfacen la ecuación $\mathbf{n} \cdot \overrightarrow{PQ} = 0$ forma un plano. La ecuación:
$$\mathbf{n} \cdot \overrightarrow{PQ} = 0$$
se conoce como la ecuación vectorial de un plano.
La ecuación escalar de un plano que contiene al punto $P = (x_0, y_0, z_0)$ con un vector normal $\mathbf{n} = \langle a, b, c \rangle$ es:
$$a(x – x_0) + b(y – y_0) + c(z – z_0) = 0.$$
Esta ecuación puede expresarse como $ax + by + cz + d = 0$, donde $d = -ax_0 – by_0 – cz_0$. Esta forma de la ecuación se denomina a veces forma general de la ecuación de un plano. ♦
Como se describió anteriormente en esta sección, los tres puntos que no están todos en la misma recta determinan un plano. Dados tres de estos puntos, podemos encontrar una ecuación para el plano que contiene estos puntos.
EJEMPLO ILUSTRATIVO 10.5_5. Escribir una ecuación de un plano dados tres puntos en el plano
Escriba una ecuación para el plano que contiene los puntos P = (1, 1, −2), Q = (0, 2, 1) y R = (- 1, −1, 0) en forma estándar y general.
Solución:
Para escribir una ecuación para un plano, debemos encontrar un vector normal para el plano. Comenzamos identificando dos vectores en el plano:
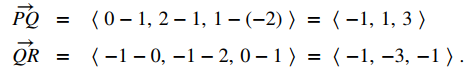
El producto cruz PQ × QR es ortogonal a ambos PQ y QR, por lo que es normal al plano que contiene estos dos vectores:
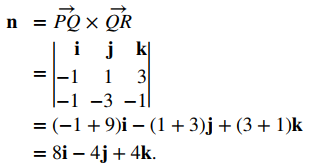
Por lo tanto, n = ⟨8, −4, 4⟩, y podemos elegir cualquiera de los tres puntos dados para escribir una ecuación del plano:
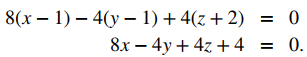
Las ecuaciones escalares de un plano varían según el vector normal y el punto elegido.
EJEMPLO ILUSTRATIVO 10.5_6. Escribir una ecuación para un plano dado un punto y una recta
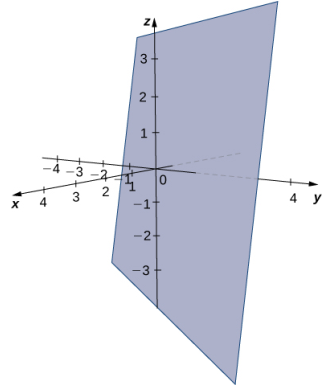
Encuentre una ecuación del plano que pasa por el punto (1, 4, 3) y contiene la recta dada por x = (y − 1)/2 = z + 1.
Solución:
Las ecuaciones simétricas describen la recta que pasa a través del punto (0, 1, −1) paralelo al vector v1 = ⟨1, 2, 1⟩ (ver la siguiente figura). Use este punto y el punto dado, (1, 4, 3), para identificar un segundo vector paralelo al plano:
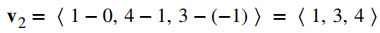
Use el producto cruz de estos vectores para identificar un vector normal para el plano:
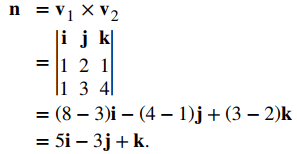
Las ecuaciones escalares para el plano son
5x − 3 (y − 1) + (z + 1) = 0 y 5x − 3y + z + 4 = 0.
Ejercicio de control 10.5.5
Halle una ecuación del plano que contiene a las rectas $L_1$ y $L_2$:
$$L_1 : x = -y = z$$ $$L_2 : \frac{x-3}{2} = y = z – 2.$$
♦Ahora que podemos escribir una ecuación para un plano, podemos usar la ecuación para encontrar la distancia d entre un punto P y el plano. Se define como la distancia más corta posible desde P hasta un punto en el plano.

Así como encontramos la distancia bidimensional entre un punto y una recta calculando la longitud de un segmento de recta perpendicular a la recta, encontramos la distancia tridimensional entre un punto y un plano calculando la longitud de un segmento de recta perpendicular al plano. Deje que R sea el punto en el plano de modo que el vector RP sea ortogonal al plano, y deje que Q sea un punto arbitrario en el plano. Luego, la proyección del vector QP sobre el vector normal describe el vector RP, como se muestra en la Figura 10.5_7.
TEOREMA 10.5_3. La distancia entre un plano y un punto
Suponga que un plano con vector normal $\mathbf{n}$ pasa por el punto $Q$. La distancia $d$ desde el plano hasta un punto $P$ que no está en el plano viene dada por:
$$d = \| \text{proj}_{\mathbf{n}} \overrightarrow{QP} \| = | \text{comp}_{\mathbf{n}} \overrightarrow{QP} | = \frac{| \overrightarrow{QP} \cdot \mathbf{n} |}{\| \mathbf{n} \|}.$$
EJEMPLO ILUSTRATIVO 10.5_7. Distancia entre un punto y un plano
Encuentre la distancia entre el punto P = (3, 1, 2) y el plano dado por x − 2y + z = 5 (vea la siguiente figura).
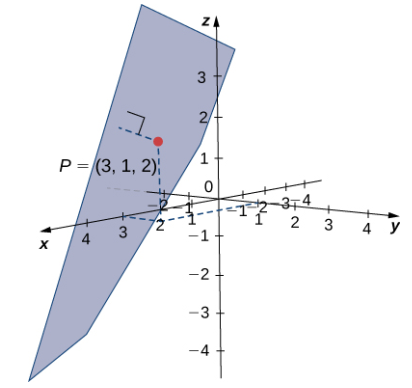
Solución:
Los coeficientes de la ecuación del plano proporcionan un vector normal para el plano: n = ⟨1, −2, 1⟩. Para encontrar el vector QP, necesitamos un punto en el plano. Cualquier punto funcionará, así que configure y = z = 0 para ver que el punto Q = (5, 0, 0) se encuentra en el plano. Encuentre la forma componente del vector de Q a P:
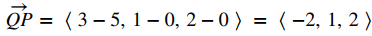
Aplique la fórmula de distancia entre un punto y un plano:
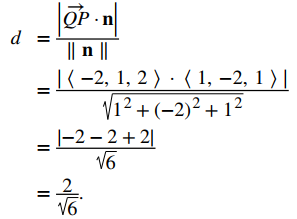
Ejercicio de control 10.5.6
Encuentra la distancia entre puntos 𝑃 = (5, −1, 0) y el plano dado por 4𝑥 +2𝑦 − 𝑧 = 3. ♦
Planos paralelos e intersectantes
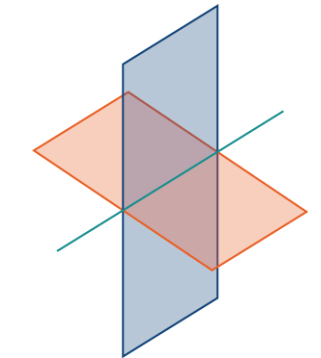
Hemos discutido las diversas relaciones posibles entre dos rectas en dos dimensiones y tres dimensiones. Cuando describimos la relación entre dos planos en el espacio, solo tenemos dos posibilidades: los dos planos distintos son paralelos o se intersecan. Cuando dos planos son paralelos, sus vectores normales son paralelos. Cuando dos planos se cruzan, la intersección es una recta (Figura 10.5_8).
EJEMPLO ILUSTRATIVO 10.5_8. Encontrar la recta de intersección para dos planos
Encuentre ecuaciones paramétricas y simétricas para la recta formada por la intersección de los planos dados por x + y + z = 0 y 2x − y + z = 0 (vea la siguiente figura).
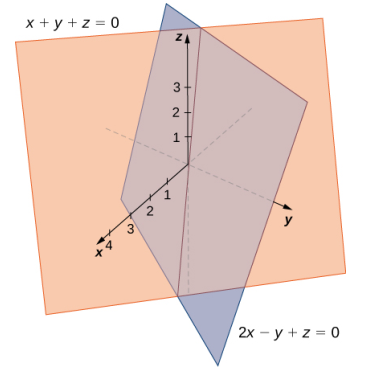
Solución:
Tenga en cuenta que los dos planos tienen normales no paralelas, por lo que los planos se intersecan. Además, el origen satisface cada ecuación, por lo que sabemos que la recta de intersección pasa a través del origen. Sume las ecuaciones planas para que podamos eliminar una de las variables, en este caso, y:
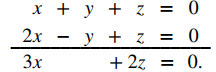
Esto nos da x = −(2/3)z. Sustituimos este valor en la primera ecuación para expresar y en términos de z:
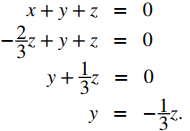
Ahora tenemos las dos primeras variables, x e y, en términos de la tercera variable, z. A continuación, definimos z en términos de t. Para eliminar la necesidad de fracciones, elegimos definir el parámetro t como t = −(1/3)z. Entonces, z = −3t. Al sustituir la representación paramétrica de z en las otras dos ecuaciones, vemos que las ecuaciones paramétricas para la recta de intersección son x = 2t, y = t, z = −3t. Las ecuaciones simétricas para la recta son x/2 = y = z/(− 3). ♦
Ejercicio de control 10.5.7
Encuentra ecuaciones paramétricas para la recta formada por la intersección de planos 𝑥 + 𝑦 − 𝑧 = 3 y 3𝑥 − 𝑦 + 3𝑧 = 5. ♦
Además de encontrar la ecuación de la recta de intersección entre dos planos, es posible que necesitemos encontrar el ángulo formado por la intersección de dos planos. Por ejemplo, los ingenieros que construyen una casa necesitan saber el ángulo donde se encuentran las diferentes secciones del techo para saber si el techo se verá bien y se drenará correctamente. Podemos usar vectores normales para calcular el ángulo entre los dos planos. Podemos hacer esto porque el ángulo entre los vectores normales es el mismo que el ángulo entre los planos. La figura 10.5_9 muestra por qué esto es cierto.
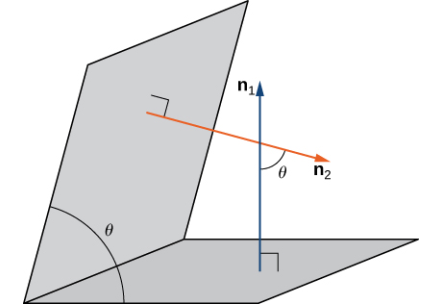
Podemos encontrar la medida del ángulo θ entre dos planos de intersección al encontrar primero el coseno del ángulo, usando la siguiente ecuación:
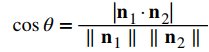
Entonces podemos usar el ángulo para determinar si dos planos son paralelos u ortogonales o si se cruzan en algún otro ángulo.
EJEMPLO ILUSTRATIVO 10.5_9. Encontrar el ángulo entre dos planos
Determine si cada par de planos es paralelo, ortogonal o ninguno. Si los planos se intersecan, pero no son ortogonales, encuentre la medida del ángulo entre ellos. Da la respuesta en radianes y redondea a dos decimales.
a) x + 2y − z = 8 y 2x + 4y − 2z = 10
b) 2x − 3y + 2z = 3 y 6x + 2y − 3z = 1
c) x + y + z = 4 y x − 3y + 5z = 1
Solución:
a) Los vectores normales para estos planos son n1 = ⟨1, 2, −1⟩ y n2 = ⟨2 ,4, −2⟩. Estos dos vectores son múltiplos escalares entre sí. Los vectores normales son paralelos, por lo que los planos son paralelos.
b) Los vectores normales para estos planos son n1 = ⟨2, −3, 2⟩ y n2 = ⟨6, 2, −3⟩. Tomando el producto punto de estos vectores, tenemos
![]()
Los vectores normales son ortogonales, por lo que los planos correspondientes también son ortogonales.
c) Los vectores normales para estos planos son n1 = ⟨1, 1 ,1⟩ y n2 = ⟨1, −3, 5⟩:
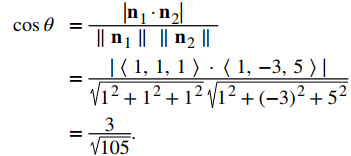
El ángulo entre los dos planos es 1.27 rad, o aproximadamente 73°. ♦
Ejercicio de control 10.5.8
Encuentra la medida del ángulo entre planos 𝑥 + 𝑦 − 𝑧 = 3 y 3𝑥 − 𝑦 + 3𝑧 = 5. Da la respuesta en radianes y redondea a dos decimales. ♦
Cuando descubrimos que dos planos son paralelos, es posible que necesitemos encontrar la distancia entre ellos. Para encontrar esta distancia, simplemente seleccionamos un punto en uno de los planos. La distancia desde este punto al otro plano es la distancia entre los planos.
Anteriormente, presentamos la fórmula para calcular esta distancia con la ecuación:
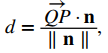
donde Q es un punto en el plano, P es un punto que no está en el plano y n es el vector normal que pasa por el punto Q. Considere la distancia desde el punto (x0, y0, z0) al plano ax + by + cz + k = 0. Sea (x1, y1, z1) cualquier punto del plano. Sustituyendo en la fórmula se obtiene
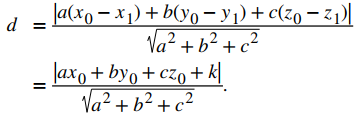
Establecemos este resultado formalmente en el siguiente teorema.
TOREMA 10.5_4. Distancia desde un punto a un plano
Sea $P(x_0, y_0, z_0)$ un punto. La distancia desde $P$ hasta el plano $ax + by + cz + k = 0$ viene dada por:
$$d = \frac{|ax_0 + by_0 + cz_0 + k|}{\sqrt{a^2 + b^2 + c^2}}.$$
EJEMPLO ILUSTRATIVO 10.5_10. Encontrar la distancia entre planos paralelos
Encuentre la distancia entre los dos planos paralelos dados por 2x + y − z = 2 y 2x + y − z = 8.
Solución:
El punto (1, 0, 0) se encuentra en el primer plano. La distancia buscada, entonces, es
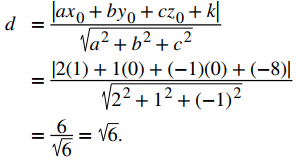
Ejercicio de control 10.5.9
Encuentra la distancia entre planos paralelos 5𝑥 − 2𝑦 + 𝑧 = 6 y 5𝑥 − 2𝑦 + 𝑧 = −3. ♦
Proyecto de Estudiantes
Distancia entre dos líneas sesgadas
Figura 10.5.10 Las instalaciones industriales de tuberías suelen presentar tuberías que van en diferentes direcciones. ¿Cómo podemos encontrar la distancia entre dos tubos torcidos?
Encontrar la distancia desde un punto hasta una línea o desde una línea hasta un plano parece un procedimiento bastante abstracto. Pero, si las líneas representan tuberías en una planta química o tubos en una refinería de petróleo o en carreteras en una intersección de autopistas, confirmar que la distancia entre ellas cumple con las especificaciones puede ser tanto importante como complicado de medir. Una forma es modelar las dos tuberías como líneas, usando las técnicas de este capítulo, y luego calcular la distancia entre ellas. El cálculo consiste en formar vectores a lo largo de las direcciones de las líneas y utilizar tanto el producto vectorial como el producto escalar.
Las formas simétricas de dos rectas, $L_1$ y $L_2$, son:
$$L_1 : \frac{x-x_1}{a_1} = \frac{y-y_1}{b_1} = \frac{z-z_1}{c_1}$$ $$L_2 : \frac{x-x_2}{a_2} = \frac{y-y_2}{b_2} = \frac{z-z_2}{c_2}.$$
Usted debe desarrollar una fórmula para la distancia $d$ entre estas dos rectas, en términos de los valores $a_1, b_1, c_1; a_2, b_2, c_2; x_1, y_1, z_1;$ y $x_2, y_2, z_2$. La distancia entre dos rectas suele entenderse como la distancia mínima, por lo que esta es la longitud de un segmento de recta o la longitud de un vector que es perpendicular a ambas rectas e interseca a ambas.
- Primero, escriba dos vectores, $\mathbf{v}_1$ y $\mathbf{v}_2$, que se encuentren a lo largo de $L_1$ y $L_2$, respectivamente.
- Halle el producto cruz de estos dos vectores y llámelo $\mathbf{N}$. Este vector es perpendicular a $\mathbf{v}_1$ y $\mathbf{v}_2$, y por lo tanto es perpendicular a ambas rectas.
- A partir del vector $\mathbf{N}$, forme un vector unitario $\mathbf{n}$ en la misma dirección.
- Use las ecuaciones simétricas para hallar un vector conveniente $\mathbf{v}_{12}$ que se encuentre entre dos puntos cualesquiera, uno en cada recta. Nuevamente, esto puede hacerse directamente a partir de las ecuaciones simétricas.
- El producto punto de dos vectores es la magnitud de la proyección de un vector sobre el otro multiplicada por la magnitud del otro vector; es decir, $\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \|\mathbf{B}\| \cos \theta$, donde $\theta$ es el ángulo entre los vectores. Usando el producto punto, halle la proyección del vector $\mathbf{v}_{12}$ hallado en el paso 4 sobre el vector unitario $\mathbf{n}$ hallado en el paso 3. Esta proyección es perpendicular a ambas rectas, y por lo tanto su longitud debe ser la distancia perpendicular $d$ entre ellas. Tenga en cuenta que el valor de $d$ puede ser negativo, dependiendo de su elección del vector $\mathbf{v}_{12}$ o del orden del producto cruz, así que use signos de valor absoluto alrededor del numerador.
- Verifique que su fórmula dé la distancia correcta de $|-25| / \sqrt{198} \approx 1.78$ entre las siguientes dos rectas:
$$L_1 : \frac{x-5}{2} = \frac{y-3}{4} = \frac{z-1}{3}$$ $$L_2 : \frac{x-6}{3} = \frac{y-1}{5} = \frac{z}{7}.$$
- ¿Es válida su expresión general cuando las rectas son paralelas? Si no, ¿por qué no? (Pista: ¿Qué sabe sobre el valor del producto cruz de dos vectores paralelos? ¿Dónde aparecería ese resultado en su expresión para $d$?)
- Demuestre que su expresión para la distancia es cero cuando las rectas se intersecan. Recuerde que dos rectas se intersecan si no son paralelas y están en el mismo plano. Por lo tanto, considere la dirección de $\mathbf{n}$ y $\mathbf{v}_{12}$. ¿Cuál es el resultado de su producto punto?
- Considere la siguiente aplicación. Los ingenieros de una refinería han determinado que necesitan instalar puntales de soporte entre muchas de las tuberías de gas para reducir las vibraciones dañinas. Para minimizar el costo, planean instalar estos puntales en los puntos más cercanos entre tuberías oblicuas adyacentes. Debido a que tienen esquemas detallados de la estructura, pueden determinar las longitudes correctas de los puntales necesarios y, por lo tanto, fabricarlos y distribuirlos a los equipos de instalación sin gastar tiempo valioso realizando mediciones.
La estructura de marco rectangular tiene las dimensiones $4.0 \times 15.0 \times 10.0 \text{ m}$ (altura, ancho y profundidad). Un sector tiene una tubería que entra por la esquina inferior de la unidad de marco estándar y sale por la esquina diametralmente opuesta (la más alejada en la parte superior); llame a esta $L_1$. Una segunda tubería entra y sale por las dos esquinas inferiores opuestas diferentes; llame a esta $L_2$.
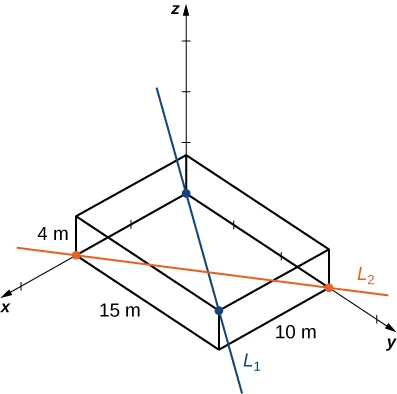
Escribe los vectores a lo largo de las líneas que representan esas tuberías, encuentra el producto vectorial entre ellos a partir del cual crear el vector unitario 𝐧, Definamos un vector que abarca dos puntos en cada línea y, finalmente, determinamos la distancia mínima entre las líneas. (Tomemos el origen en la esquina inferior del primer tubo.) De manera similar, también puedes desarrollar las ecuaciones simétricas para cada línea y sustituirlas directamente en tu fórmula.

y si me dan la distancia entre esos dos puntos para que la necesito? Debo usarla para resolver la ecuación algebraica?
Un aporte muy interesante. Gracias por la información. Saludos.
Con gusto, bienvenida! 👍😺
Wow eso fue extraño. Acabo de escribir un comentario increíblemente largo, pero después de hacer clic en enviar, mi comentario no apareció. Grrrr … bueno, no voy a escribir todo eso otra vez. De todos modos, solo quería decir blog fantástico!
jajaja, a veces suceden esos inconvenientes, gracias por tomarte el tiempo en escribir.