En los siguientes ejercicios, se dan los puntos $P$ y $Q$. Sea $L$ la recta que pasa por los puntos $P$ y $Q$.

1. Halle la ecuación vectorial de la recta $L$.
2. Halle las ecuaciones paramétricas de la recta $L$.
3. Halle las ecuaciones simétricas de la recta $L$.
4. Halle las ecuaciones paramétricas del segmento de recta determinado por $P$ y $Q$.

243. $P(-3, 5, 9), \quad Q(4, -7, 2)$

244. $P(4, 0, 5), \quad Q(2, 3, 1)$

245. $P(-1, 0, 5), \quad Q(4, 0, 3)$

246. $P(7, -2, 6), \quad Q(-3, 0, 6)$

Para los siguientes ejercicios, se dan el punto $P$ y el vector $\mathbf{v}$. Sea $L$ la recta que pasa por el punto $P$ con dirección $\mathbf{v}$.

1. Halle las ecuaciones paramétricas de la recta $L$.
2. Halle las ecuaciones simétricas de la recta $L$.
3. Halle la intersección de la recta con el plano $xy$.

247. $P(1, -2, 3), \quad \mathbf{v} = \langle 1, 2, 3 \rangle$

248. $P(3, 1, 5), \quad \mathbf{v} = \langle 1, 1, 1 \rangle$

249. $P(3, 1, 5), \quad \mathbf{v} = \overrightarrow{QR}, \text{ donde } Q(2, 2, 3) \text{ y } R(3, 2, 3)$

250. $P(2, 3, 0), \quad \mathbf{v} = \overrightarrow{QR}, \text{ donde } Q(0, 4, 5) \text{ y } R(0, 4, 6)$

Para los siguientes ejercicios, se da la recta $L$.

1. Halle el punto $P$ que pertenece a la recta y el vector director $\mathbf{v}$ de la recta. Exprese $\mathbf{v}$ en forma de componentes.
2. Halle la distancia desde el origen hasta la recta $L$.

251. $x = 1 + t, \quad y = 3 + t, \quad z = 5 + 4t, \quad t \in \mathbb{R}$

252. $-x = y + 1, \quad z = 2$

253. Halle la distancia entre el punto $A(-3, 1, 1)$ y la recta de ecuaciones simétricas $x = -y = -z$.

254. Halle la distancia entre el punto $A(4, 2, 5)$ y la recta de ecuaciones paramétricas $x = -1 – t, \quad y = -t, \quad z = 2, \quad t \in \mathbb{R}$.

Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$.

1. Verifique si las rectas $L_1$ y $L_2$ son paralelas.
2. Si las rectas $L_1$ y $L_2$ son paralelas, halle la distancia entre ellas.

255. $L_1 : x = 1 + t, \ y = t, \ z = 2 + t, \ t \in \mathbb{R}; \ L_2 : x – 3 = y – 1 = z – 3$

256. $L_1 : x = 2, \ y = 1, \ z = t; \ L_2 : x = 1, \ y = 1, \ z = 2 – 3t, \ t \in \mathbb{R}$

257. Demuestre que la recta que pasa por los puntos $P(3, 1, 0)$ y $Q(1, 4, -3)$ es perpendicular a la recta con ecuación $x = 3t, \ y = 3 + 8t, \ z = -7 + 6t, \ t \in \mathbb{R}$.

258. ¿Son las rectas de ecuaciones $x = -2 + 2t, \ y = -6, \ z = 2 + 6t$ y $x = -1 + t, \ y = 1 + t, \ z = t, \ t \in \mathbb{R}$, perpendiculares entre sí?

259. Halle el punto de intersección de las rectas de ecuaciones $x = -2y = 3z$ y $x = -5 – t, \ y = -1 + t, \ z = t – 11, \ t \in \mathbb{R}$.

260. Halle el punto de intersección del eje $x$ con la recta de ecuaciones paramétricas $x = 10 + t, \ y = 2 – 2t, \ z = -3 + 3t, \ t \in \mathbb{R}$.

Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$. Determine si las rectas son iguales, paralelas pero no iguales, oblicuas (skew) o secantes.

261. $L_1 : x = y – 1 = -z \quad \text{y} \quad L_2 : x – 2 = -y = \frac{z}{2}$

262. $L_1 : x = 2t, y = 0, z = 3, t \in \mathbb{R} \quad \text{and} \quad L_2 : x = 0, y = 8 + s, z = 7 + s, s \in \mathbb{R}$

263. $L_1 : x = -1 + 2t, y = 1 + 3t, z = 7t, t \in \mathbb{R} \quad \text{and} \quad L_2 : x – 1 = \frac{2}{3}(y – 4) = \frac{2}{7}z – 2$

264. $L_1 : 3x = y + 1 = 2z \quad \text{and} \quad L_2 : x = 6 + 2t, y = 17 + 6t, z = 9 + 3t, t \in \mathbb{R}$

265. Considere la recta $L$ de ecuaciones simétricas $x – 2 = -y = \frac{z}{2}$ y el punto $A(1, 1, 1)$.

1. Halle las ecuaciones paramétricas de una recta paralela a $L$ que pase por el punto $A$.
2. Halle las ecuaciones simétricas de una recta oblicua (skew) a $L$ que pase por el punto $A$.
3. Halle las ecuaciones simétricas de una recta que interseque a $L$ y pase por el punto $A$.

266. Considere la recta $L$ de ecuaciones paramétricas $x = t, y = 2t, z = 3, t \in \mathbb{R}$.

1. Halle las ecuaciones paramétricas de una recta paralela a $L$ que pase por el origen.
2. Halle las ecuaciones paramétricas de una recta oblicua (skew) a $L$ que pase por el origen.
3. Halle las ecuaciones simétricas de una recta que interseque a $L$ y pase por el origen.

Para los siguientes ejercicios, se dan el punto $P$ y el vector normal $\mathbf{n}$.

1. Halle la ecuación escalar del plano que pasa por $P$ y tiene vector normal $\mathbf{n}$.
2. Halle la forma general de la ecuación del plano que pasa por $P$ y tiene vector normal $\mathbf{n}$.

267. $P(0, 0, 0), \quad \mathbf{n} = 3\mathbf{i} – 2\mathbf{j} + 4\mathbf{k}$

268. $P(3, 2, 2), \quad \mathbf{n} = 2\mathbf{i} + 3\mathbf{j} – \mathbf{k}$

269. $P(1, 2, 3), \quad \mathbf{n} = \langle 1, 2, 3 \rangle$

270. $P(0, 0, 0), \quad \mathbf{n} = \langle -3, 2, -1 \rangle$

Para los siguientes ejercicios, se da la ecuación de un plano.

1. Halle el vector normal $\mathbf{n}$ al plano. Exprese $\mathbf{n}$ utilizando vectores unitarios estándar.
2. Halle las intersecciones del plano con los ejes coordenados.
3. Esboce el plano.

271. [T] $4x + 5y + 10z – 20 = 0$

272. $3x + 4y – 12 = 0$

273. $3x – 2y + 4z = 0$

274. $x + z = 0$

275. Dado el punto $P(1, 2, 3)$ y el vector $\mathbf{n} = \mathbf{i} + \mathbf{j}$, halle un punto $Q$ en el eje $x$ tal que $\overrightarrow{PQ}$ y $\mathbf{n}$ sean ortogonales.

276. Muestre que no existe un plano perpendicular a $\mathbf{n} = \mathbf{i} + \mathbf{j}$ que pase por los puntos $P(1, 2, 3)$ y $Q(2, 3, 4)$.

277. Halle las ecuaciones paramétricas de la recta que pasa por el punto $P(-2, 1, 3)$ y es perpendicular al plano de ecuación $2x – 3y + z = 7$.

278. Halle las ecuaciones simétricas de la recta que pasa por el punto $P(2, 5, 4)$ y es perpendicular al plano de ecuación $2x + 3y – 5z = 0$.

279. Muestre que la recta $\frac{x-1}{2} = \frac{y+1}{3} = \frac{z-2}{4}$ es paralela al plano $x – 2y + z = 6$.

280. Halle el número real $\alpha$ tal que la recta de ecuaciones paramétricas $x = t, y = 2 – t, z = 3 + t, t \in \mathbb{R}$ es paralela al plano de ecuación $\alpha x + 5y + z – 10 = 0$.

Para los siguientes ejercicios, se dan los puntos $P$, $Q$ y $R$.

1. Halle la ecuación general del plano que pasa por $P$, $Q$ y $R$.
2. Escriba la ecuación vectorial $\mathbf{n} \cdot \overrightarrow{PS} = 0$ del plano en el inciso a., donde $S(x, y, z)$ es un punto arbitrario del plano.
3. Halle las ecuaciones paramétricas de la recta que pasa por el origen y es perpendicular al plano que pasa por $P$, $Q$ y $R$.

281. $P(1, 1, 1), \quad Q(2, 4, 3), \quad \text{y} \quad R(-1, -2, -1)$

282. $P(-2, 1, 4), \quad Q(3, 1, 3), \quad \text{y} \quad R(-2, 1, 0)$

283. Considere los planos de ecuaciones $x + y + z = 1$ y $x + z = 0$.

1. Demuestre que los planos se intersecan.
2. Halle las ecuaciones simétricas de la recta que pasa por el punto $P(1, 4, 6)$ y es paralela a la recta de intersección de los planos.

284. Considere los planos de ecuaciones $-y + z – 2 = 0$ y $x – y = 0$.

1. Demuestre que los planos se intersecan.
2. Halle las ecuaciones paramétricas de la recta que pasa por el punto $P(-8, 0, 2)$ y es paralela a la recta de intersección de los planos.

285. Halle la ecuación escalar del plano que pasa por el punto $P(-1, 2, 1)$ y es perpendicular a la recta de intersección de los planos $x + y – z – 2 = 0$ y $2x – y + 3z – 1 = 0$.

286. Halle la ecuación general del plano que pasa por el origen y es perpendicular a la recta de intersección de los planos $-x + y + 2 = 0$ y $z – 3 = 0$.

287. Determine si la recta de ecuaciones paramétricas $x = 1 + 2t, \ y = -2t, \ z = 2 + t, \ t \in \mathbb{R}$ interseca al plano de ecuación $3x + 4y + 6z – 7 = 0$. Si se intersecan, halle el punto de intersección.

288. Determine si la recta de ecuaciones paramétricas $x = 5, \ y = 4 – t, \ z = 2t, \ t \in \mathbb{R}$ interseca al plano de ecuación $2x – y + z = 5$. Si se intersecan, halle el punto de intersección.

289. Halle la distancia desde el punto $P(1, 5, -4)$ al plano de ecuación $3x – y + 2z – 6 = 0$.

290. Halle la distancia desde el punto $P(1, -2, 3)$ al plano de ecuación $(x – 3) + 2(y + 1) – 4z = 0$.

Para los siguientes ejercicios, se dan las ecuaciones de dos planos.

1. Determine si los planos son paralelos, ortogonales o ninguno de los dos.
2. Si los planos no son ni paralelos ni ortogonales, halle la medida del ángulo entre los planos. Exprese la respuesta en grados redondeada al entero más cercano.

291. [T] $x + y + z = 0, \quad 2x – y + z – 7 = 0$

292. $5x – 3y + z = 4, \quad x + 4y + 7z = 1$

293. $x – 5y – z = 1, \quad 5x – 25y – 5z = -3$

294. [T] $x – 3y + 6z = 4, \quad 5x + y – z = 4$

295. Demuestre que las rectas de ecuaciones $x = t, \ y = 1 + t, \ z = 2 + t, \ t \in \mathbb{R}$, y $\frac{x}{2} = \frac{y-1}{3} = z – 3$ son oblicuas (skew), y halle la distancia entre ellas.

296. Demuestre que las rectas de ecuaciones $x = -1 + t, \ y = -2 + t, \ z = 3t, \ t \in \mathbb{R}$, y $x = 5 + s, \ y = -8 + 2s, \ z = 7s, \ s \in \mathbb{R}$ son oblicuas (skew), y halle la distancia entre ellas.

297. Considere el punto $C(-3, 2, 4)$ y el plano de ecuación $2x + 4y – 3z = 8$.

1. Halle el radio de la esfera con centro $C$ tangente al plano dado.
2. Halle el punto $P$ de tangencia.

298. Considere el plano de ecuación $x – y – z – 8 = 0$.

1. Halle la ecuación de la esfera con centro $C$ en el origen que es tangente al plano dado.
2. Halle las ecuaciones paramétricas de la recta que pasa por el origen y el punto de tangencia.

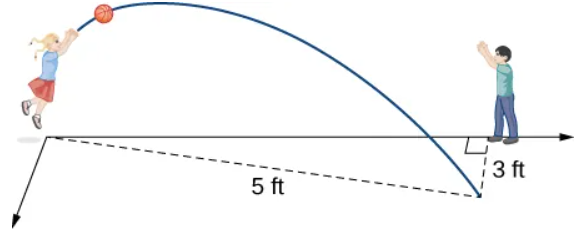
299. Dos niños juegan con una pelota. La niña lanza la pelota al niño. La pelota viaja por el aire, se curva $3 \text{ ft}$ hacia la derecha y cae a $5 \text{ ft}$ de distancia de la niña (ver la siguiente figura). Si el plano que contiene la trayectoria de la pelota es perpendicular al suelo, halle su ecuación.

300. [T] John asigna $d$ dólares para consumir mensualmente tres bienes de precios $a, b, \text{ y } c$. En este contexto, la ecuación de presupuesto se define como $ax + by + cz = d$, donde $x \geq 0, y \geq 0, \text{ y } z \geq 0$ representan el número de artículos comprados de cada uno de los bienes. El conjunto presupuestario viene dado por $\{(x, y, z) \mid ax + by + cz \leq d, x \geq 0, y \geq 0, z \geq 0\}$, y el plano presupuestario es la parte del plano de ecuación $ax + by + cz = d$ para la cual $x \geq 0, y \geq 0, \text{ y } z \geq 0$. Considere $a = \$8, b = \$5, c = \$10, \text{ y } d = \$500$.

1. Use un CAS (Sistema de Álgebra Computacional) para graficar el conjunto presupuestario y el plano presupuestario.
2. Para $z = 25$, halle la nueva ecuación de presupuesto y grafique el conjunto presupuestario en el mismo sistema de coordenadas.

301. [T] Considere $\mathbf{r}(t) = \langle \sin t, \cos t, 2t \rangle$ como el vector de posición de una partícula al tiempo $t \in [0, 3]$, donde las componentes de $\mathbf{r}$ se expresan en centímetros y el tiempo se mide en segundos. Sea $\overrightarrow{OP}$ el vector de posición de la partícula después de $1 \text{ seg}$.

1. Determine el vector velocidad $\mathbf{v}(1)$ de la partícula después de $1 \text{ seg}$.
2. Halle la ecuación escalar del plano que es perpendicular a $\mathbf{v}(1)$ y pasa por el punto $P$. Este plano se denomina plano normal a la trayectoria de la partícula en el punto $P$.
3. Use un CAS para visualizar la trayectoria de la partícula junto con el vector velocidad y el plano normal en el punto $P$.

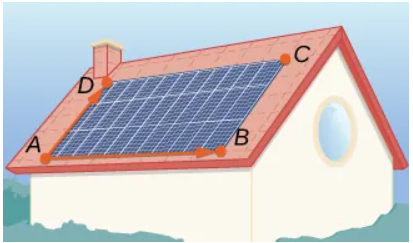
302. [T] Un panel solar se instala en el techo de una casa. El panel puede considerarse posicionado en los puntos de coordenadas (en metros) $A(8, 0, 0), B(8, 18, 0), C(0, 18, 8), \text{ y } D(0, 0, 8)$.

1. Halle la forma general de la ecuación del plano que contiene al panel solar utilizando los puntos $A, B, \text{ y } C$, y demuestre que su vector normal es equivalente a $\overrightarrow{AB} \times \overrightarrow{AD}$.
2. Halle las ecuaciones paramétricas de la recta $L_1$ que pasa por el centro del panel solar y tiene un vector director $\mathbf{s} = \frac{1}{\sqrt{3}}\mathbf{i} + \frac{1}{\sqrt{3}}\mathbf{j} + \frac{1}{\sqrt{3}}\mathbf{k}$, el cual apunta hacia la posición del Sol en un momento particular del día.
3. Halle las ecuaciones simétricas de la recta $L_2$ que pasa por el centro del panel solar y es perpendicular a este.
4. Determine el ángulo de elevación del Sol sobre el panel solar utilizando el ángulo entre las rectas $L_1 \text{ y } L_2$.