| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.7 |

10.7 COORDENADAS CILÍNDRICAS Y ESFÉRICAS: Objetivos de aprendizaje

10.7.1. Convierte de coordenadas cilíndricas a rectangulares.
10.7.2. Convierte de coordenadas rectangulares a cilíndricas.
10.7.3. Convierte de coordenadas esféricas a rectangulares.
10.7.4. Convierte de coordenadas rectangulares a esféricas.

El sistema de coordenadas cartesianas proporciona una forma sencilla de describir la ubicación de los puntos en el espacio. Sin embargo, algunas superficies pueden ser difíciles de modelar con ecuaciones basadas en el sistema cartesiano. Este es un problema familiar; recuerde que en dos dimensiones, las coordenadas polares a menudo proporcionan un sistema alternativo útil para describir la ubicación de un punto en el plano, particularmente en casos que involucran círculos. En esta sección, veremos dos formas diferentes de describir la ubicación de los puntos en el espacio, ambas basadas en extensiones de coordenadas polares. Como su nombre lo indica, las coordenadas cilíndricas son útiles para tratar problemas que involucran cilindros, como calcular el volumen de un tanque de agua redondo o la cantidad de aceite que fluye a través de una tubería. Del mismo modo, las coordenadas esféricas son útiles para tratar problemas relacionados con esferas, como encontrar el volumen de estructuras abovedadas.

Coordenadas Cilíndricas

Cuando expandimos el sistema tradicional de coordenadas cartesianas de dos dimensiones a tres, simplemente agregamos un nuevo eje para modelar la tercera dimensión. Comenzando con coordenadas polares, podemos seguir este mismo proceso para crear un nuevo sistema de coordenadas tridimensional, llamado sistema de coordenadas cilíndricas. De esta manera, las coordenadas cilíndricas proporcionan una extensión natural de las coordenadas polares a tres dimensiones.

DEFINICIÓN. Sistema de coordenadas cilíndricas

En el sistema de coordenadas cilíndricas, un punto en el espacio (Figura 10.7_1) está representado por el triple ordenado (r, θ, z), donde

♦ (r, θ) son las coordenadas polares de la proyección del punto en el plano xy
♦ z es la coordenada z habitual en el sistema de coordenadas cartesianas.

En el plano xy, el triángulo rectángulo que se muestra en la figura 10.7_1 proporciona la clave para la transformación entre coordenadas cilíndricas y cartesianas, o rectangulares.

TEOREMA 140.7.1. Conversión entre coordenadas cilíndricas y cartesianas

Las coordenadas rectangulares $(x, y, z)$ y las coordenadas cilíndricas $(r, \theta, z)$ de un punto se relacionan de la siguiente manera:

$\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ z &= z \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas cilíndricas a coordenadas rectangulares.
y
$\begin{align} r^2 &= x^2 + y^2 \\ \tan \theta &= \frac{y}{x} \\ z &= z \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas rectangulares a coordenadas cilíndricas.

♦

Como cuando discutimos la conversión de coordenadas rectangulares a coordenadas polares en dos dimensiones, debe notarse que la ecuación tanθ = y/x tiene un número infinito de soluciones. Sin embargo, si restringimos θ a valores entre 0 y 2π, entonces podemos encontrar una solución única basada en el cuadrante del plano xy en el que se encuentra el punto original (x, y, z). Tenga en cuenta que si x = 0, entonces el valor de θ es π/2,3π/2 o 0, dependiendo del valor de y.

Observe que estas ecuaciones se derivan de las propiedades de los triángulos rectángulos. Para que sea fácil de ver, considere el punto P en el plano xy con coordenadas rectangulares (x, y, 0) y con coordenadas cilíndricas (r, θ, 0), como se muestra en la siguiente figura.

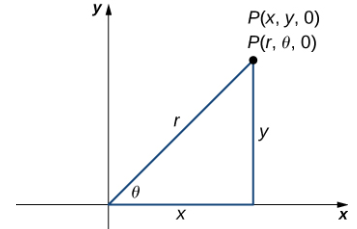
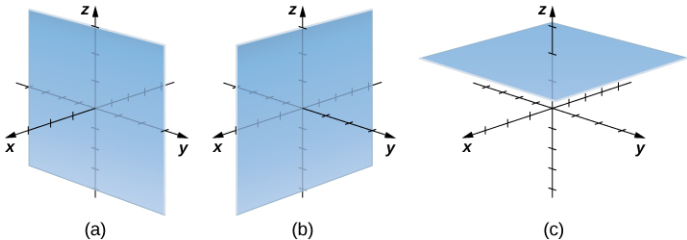
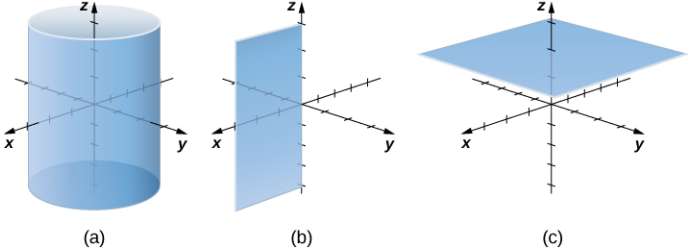
       Consideremos las diferencias entre las coordenadas rectangulares y cilíndricas al observar las superficies generadas cuando cada una de las coordenadas se mantiene constante. Si c es una constante, entonces en coordenadas rectangulares, las superficies de la forma x = c, y = c, o z = c son todos planos. Los planos de estas formas son paralelos al plano yz, al plano xz y al plano xy, respectivamente. Cuando convertimos a coordenadas cilíndricas, la coordenada z no cambia. Por lo tanto, en coordenadas cilíndricas, las superficies de la forma z = c son planos paralelos al plano xy. Ahora, pensemos en las superficies de la forma r = c. Los puntos en estas superficies están a una distancia fija del eje z. En otras palabras, estas superficies son cilindros circulares verticales. Por último, ¿qué pasa con θ = c? Los puntos en una superficie de la forma θ = c están en un ángulo fijo desde el eje x, lo que nos da un semiplano que comienza en el eje z (Figura 10.7_3 y Figura 10.7_4).

EJEMPLO ILUSTRATIVO 10.7_1. Conversión de coordenadas cilíndricas a rectangulares

Trace el punto con coordenadas cilíndricas (4, 2π/3, −2) y exprese su ubicación en coordenadas rectangulares.

Solución:

La conversión de coordenadas cilíndricas a rectangulares requiere una aplicación simple de las ecuaciones numeradas en “Conversión entre coordenadas cilíndricas y cartesianas”:

El punto con coordenadas cilíndricas (4, 2π/3, −2) tiene coordenadas rectangulares (−2, 2√3, −2) (ver la siguiente figura).

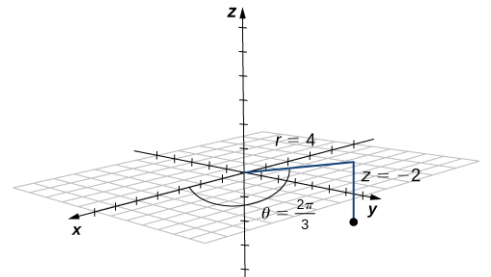
Figura 10.7_5 La proyección del punto en el plano xy es de 4 unidades desde el origen. La línea desde el origen hasta la proyección del punto forma un ángulo de 2π/3 con el eje x positivo. El punto se encuentra 2 unidades debajo del plano xy.

Si este proceso parece familiar, es con buena razón. Este es exactamente el mismo proceso que seguimos en “Introducción a las ecuaciones paramétricas y las coordenadas polares” para convertir de coordenadas polares a coordenadas rectangulares bidimensionales.

Ejercicio de control 10.7.1

El punto $R$ tiene coordenadas cilíndricas $(5, \frac{\pi}{6}, 4)$. Grafique $R$ y describa su ubicación en el espacio utilizando coordenadas rectangulares o cartesianas. ♦

EJEMPLO ILUSTRATIVO 10.7_2 Conversión de coordenadas rectangulares a cilíndricas

Convierta las coordenadas rectangulares (1, −3, 5) en coordenadas cilíndricas.

Solución:

Use el segundo conjunto de ecuaciones de Conversión entre coordenadas cilíndricas y cartesianas para traducir de coordenadas rectangulares a coordenadas cilíndricas:

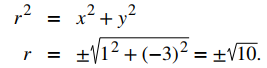
Elegimos la raíz cuadrada positiva, entonces r = √10. Ahora, aplicamos la fórmula para encontrar θ. En este caso, y es negativo y x es positivo, lo que significa que debemos seleccionar el valor de θ entre 3π/2 y 2π:

En este caso, las coordenadas z son las mismas en coordenadas rectangulares y cilíndricas:

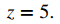
El punto con coordenadas rectangulares (1, −3, 5) tiene coordenadas cilíndricas aproximadamente iguales a (√10, 5.03, 5).

El uso de coordenadas cilíndricas es común en campos como la física. Los físicos que estudian las cargas eléctricas y los condensadores utilizados para almacenar estas cargas han descubierto que estos sistemas a veces tienen una simetría cilíndrica. Estos sistemas tienen ecuaciones de modelado complicadas en el sistema de coordenadas cartesianas, lo que dificulta su descripción y análisis. Las ecuaciones a menudo se pueden expresar en términos más simples usando coordenadas cilíndricas. Por ejemplo, el cilindro descrito por la ecuación x² + y² = 25 en el sistema cartesiano puede representarse mediante la ecuación cilíndrica r = 5.

Ejercicio de control 10.7.2

Punto de conversión (−8, 8, −7) desde coordenadas cartesianas hasta coordenadas cilíndricas. ♦

EJEMPLO ILUSTRATIVO 10.7_3 Identificación de superficies en el sistema de coordenadas cilíndricas

Describa las superficies con las ecuaciones cilíndricas dadas.

Solución:
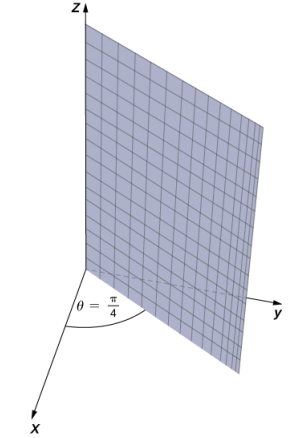
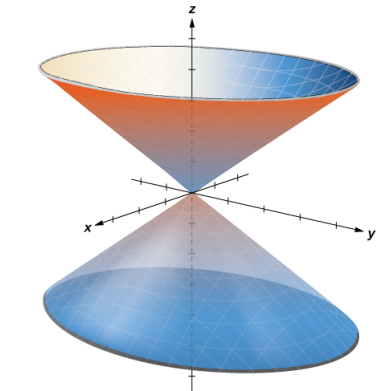
a. Cuando el ángulo θ se mantiene constante mientras r y z pueden variar, el resultado es un semiplano (ver la siguiente figura).

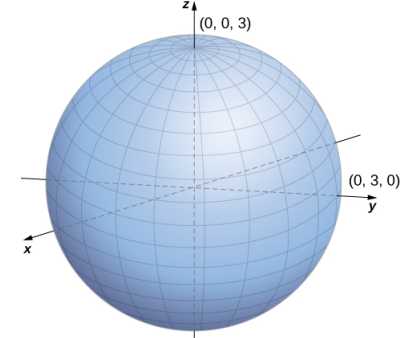
b. Sustituya r^2 = x^2 + y^2 en la ecuación r^2 + z^2 = 9 para expresar la forma rectangular de la ecuación: x^2 + y^2 + z^2 = 9. Esta ecuación describe una esfera centrada en el origen con radio 3 (ver la siguiente figura).

c. Para describir la superficie definida por la ecuación z = r, ¿es útil examinar trazas paralelas al plano xy? Por ejemplo, la traza en el plano z = 1 es la circunferencia r = 1, la traza en el plano z = 3 es la circunferencia r = 3, y así sucesivamente. Cada rastro es una circunferencia. A medida que aumenta el valor de z, el radio de la circunferencia también aumenta. La superficie resultante es un cono (ver la siguiente figura).

Ejercicio de control 10.7.3

Describe la superficie con una ecuación cilíndrica 𝑟 = 6. ♦

Coordenadas Esféricas

En el sistema de coordenadas cartesianas, la ubicación de un punto en el espacio se describe utilizando un triple ordenado en el que cada coordenada representa una distancia. En el sistema de coordenadas cilíndricas, la ubicación de un punto en el espacio se describe utilizando dos distancias (r y z) y una medida de ángulo (θ). En el sistema de coordenadas esféricas, nuevamente usamos un triple ordenado para describir la ubicación de un punto en el espacio. En este caso, el triple describe una distancia y dos ángulos. Las coordenadas esféricas facilitan la descripción de una esfera, al igual que las coordenadas cilíndricas facilitan la descripción de un cilindro. Las líneas de cuadrícula para coordenadas esféricas se basan en medidas de ángulo, como las de coordenadas polares.

DEFINICIÓN. Sistema de coordenadas esféricas

En el sistema de coordenadas esféricas, un punto P en el espacio (Figura 10.7_9) está representado por el triple ordenado (ρ, θ, φ) donde

♦ ρ (la letra griega rho) es la distancia entre P y el origen (ρ ≠ 0);
♦ θ es el mismo ángulo utilizado para describir la ubicación en coordenadas cilíndricas;
♦ φ (la letra griega phi) es el ángulo formado por el eje z positivo y el segmento de recta OP, donde O es el origen y 0 ≤ φ ≤ π. ♦

Por convención, el origen se representa como (0, 0, 0) en coordenadas esféricas.

TEOREMA 10.72. Conversión entre coordenadas esféricas, cilíndricas y rectangulares

Las coordenadas rectangulares $(x, y, z)$ y las coordenadas esféricas $(\rho, \theta, \varphi)$ de un punto se relacionan de la siguiente manera:

$\begin{align} x &= \rho \sin \varphi \cos \theta \\ y &= \rho \sin \varphi \sin \theta \\ z &= \rho \cos \varphi \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas esféricas a coordenadas rectangulares.
y
$\begin{align} \rho^2 &= x^2 + y^2 + z^2 \\ \tan \theta &= \frac{y}{x} \\ \varphi &= \arccos \left( \frac{z}{\sqrt{x^2+y^2+z^2}} \right) \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas rectangulares a coordenadas esféricas.

Si un punto tiene coordenadas cilíndricas $(r, \theta, z)$, entonces estas ecuaciones definen la relación entre las coordenadas cilíndricas y esféricas.

$\begin{align} r &= \rho \sin \varphi \\ \theta &= \theta \\ z &= \rho \cos \varphi \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas esféricas a coordenadas cilíndricas.
y
$\begin{align} \rho &= \sqrt{r^2 + z^2} \\ \theta &= \theta \\ \varphi &= \arccos \left( \frac{z}{\sqrt{r^2+z^2}} \right) \end{align}$	Estas ecuaciones se utilizan para convertir de coordenadas cilíndricas a coordenadas esféricas.

♦

Las fórmulas para convertir de coordenadas esféricas a coordenadas rectangulares pueden parecer complejas, pero son aplicaciones sencillas de trigonometría. Mirando la figura 10.7_10, es fácil ver que r = ρsenφ. Luego, mirando el triángulo en el plano xy con r como su hipotenusa, tenemos x = rcosθ = ρsenφcosθ. La derivación de la fórmula para y es similar. La figura 107_8 también muestra que ρ² = r² + z² = x² + y² + z²  y  z = ρcosφ. Resolviendo esta última ecuación para φ y luego sustituyendo ρ = √(r² + z² ) (de la primera ecuación) produce φ = arccos (z/√(r² + z² )). Además, tenga en cuenta que, como antes, debemos tener cuidado al usar la fórmula tanθ = y /x para elegir el valor correcto de θ.

Como hicimos con las coordenadas cilíndricas, consideremos las superficies que se generan cuando cada una de las coordenadas se mantiene constante. Deje que c sea una constante y considere las superficies de la forma ρ = c. Los puntos en estas superficies están a una distancia fija del origen y forman una esfera. La coordenada θ en el sistema de coordenadas esféricas es la misma que en el sistema de coordenadas cilíndricas, por lo que las superficies de la forma θ = c son semiplanos, como antes. Por último, considere las superficies de la forma φ = c. Los puntos en estas superficies están en un ángulo fijo desde el eje z y forman un medio cono (Figura 10.7_11).

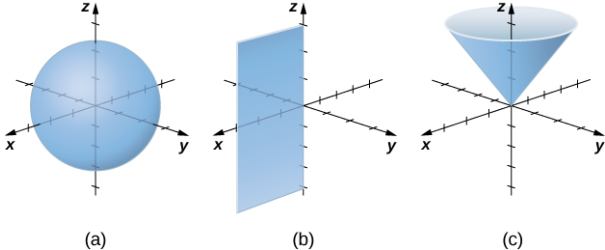
Figura 10.7_11 (a) En coordenadas esféricas, las superficies de la forma ρ = c son esferas de radio ρ, (b) las superficies de la forma θ = c son semiplanos en un ángulo θ desde el eje x  y (c) las superficies de la forma ϕ = c son medios conos en un ángulo ϕ desde el eje z.

EJEMPLO ILUSTRATIVO 10.7_4  Conversión de coordenadas esféricas

Trace el punto con coordenadas esféricas (8, π/3, π/6) y exprese su ubicación en coordenadas rectangulares y cilíndricas.

Solución:

Use las ecuaciones en “Conversión entre coordenadas esféricas, cilíndricas y rectangulares” para convertir entre coordenadas esféricas y cilíndricas (Figura 10.7_12):

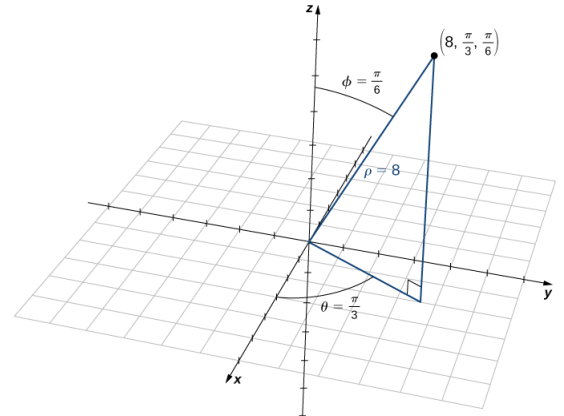
El punto con coordenadas esféricas (8, π/3, π/6) tiene coordenadas rectangulares (2, 2√3, 4√3).
Encontrar los valores en coordenadas cilíndricas es igualmente sencillo:

Por lo tanto, las coordenadas cilíndricas para el punto son (4, π/3, 4√3).

Ejercicio de control 10.7.4

Grafique el punto con coordenadas esféricas $\left( 2, -\frac{5\pi}{6}, \frac{\pi}{6} \right)$ y describa su ubicación tanto en coordenadas rectangulares como cilíndricas. ♦

EJEMPLO ILUSTRATIVO 10.7_5 Conversión de coordenadas rectangulares

Convierta las coordenadas rectangulares (−1, 1, √6) en coordenadas esféricas y cilíndricas.

Solución:

Comience convirtiendo de coordenadas rectangulares a esféricas:

Como (x, y) = (- 1, 1), la elección correcta para θ es 3π/4.

En realidad, hay dos formas de identificar φ. Podemos usar la ecuación

Sin embargo, un enfoque más simple es usar la ecuación z = ρcosφ. Sabemos que z = √6  y  ρ = 2√2, entonces

y por lo tanto φ = π/6. Las coordenadas esféricas del punto son (2√2, 3π/4, π/6).

Para encontrar las coordenadas cilíndricas para el punto, solo necesitamos encontrar r:

Las coordenadas cilíndricas para el punto son (√2, 3π/4, √6).

EJEMPLO ILUSTRATIVO 10.7_6 Identificación de superficies en el sistema de coordenadas esféricas

Describe las superficies con las ecuaciones esféricas dadas.

Solución:
a. La variable θ representa la medida del mismo ángulo en los sistemas de coordenadas cilíndricos y esféricas. Los puntos con coordenadas (ρ, π/3, φ) se encuentran en el plano que forma el ángulo θ = π/3 con el eje x positivo. Como ρ > 0, la superficie descrita por la ecuación θ = π/3 es el semiplano que se muestra en la figura 10.7_13.

b. La ecuación φ = 5π/6 describe todos los puntos en el sistema de coordenadas esféricas que se encuentran en una recta desde el origen formando un ángulo que mide 5π/6 rad con el eje z positivo. Estos puntos forman un medio cono (Figura 10.7_14). Debido a que solo hay un valor para φ que se mide desde el eje z positivo, no obtenemos el cono completo (con dos piezas).

Para encontrar la ecuación en coordenadas rectangulares, usa la ecuación

Esta es la ecuación de un cono centrado en el eje z.

c. La ecuación ρ = 6 describe el conjunto de todos los puntos a 6 unidades del origen: una esfera con radio 6 (Figura 10.7_15).

d. Para identificar esta superficie, convierta la ecuación de coordenadas esféricas a rectangulares, utilizando las ecuaciones y = ρsenφsenθ y ρ² = x² + y² + z²:

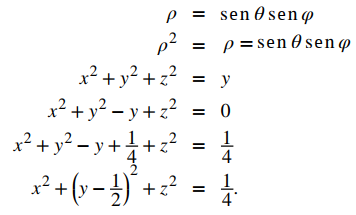
La ecuación describe una esfera centrada en el punto (0, 1/2, 0) con radio 1/2.

Ejercicio de control 10.7.5

Describa las superficies definidas por las siguientes ecuaciones:

♦

       Las coordenadas esféricas son útiles para analizar sistemas que tienen cierto grado de simetría sobre un punto, como el volumen del espacio dentro de un estadio abovedado o la velocidad del viento en la atmósfera de un planeta. Una esfera que tiene la ecuación cartesiana x² + y² + z² = c² tiene la ecuación simple ρ = c en coordenadas esféricas.

En geografía, la latitud y la longitud se utilizan para describir ubicaciones en la superficie de la Tierra, como se muestra en la Figura 10.7_16. Aunque la forma de la Tierra no es una esfera perfecta, utilizamos coordenadas esféricas para comunicar la ubicación de los puntos en la Tierra. Supongamos que la Tierra tiene la forma de una esfera con un radio de 4000 mi. Expresamos las medidas de los ángulos en grados en lugar de radianes porque la latitud y la longitud se miden en grados.

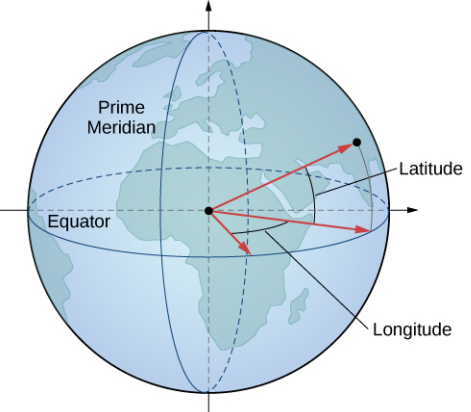
Deje que el centro de la Tierra sea el centro de la esfera, con el rayo desde el centro a través del Polo Norte que representa el eje z positivo. El meridiano principal representa el rastro de la superficie a medida que se cruza con el plano xz. El ecuador es la traza de la esfera que se cruza con el plano xy.

EJEMPLO ILUSTRATIVO 10.7_7 Conversión de latitud y longitud a coordenadas esféricas

La latitud de Columbus, Ohio, es de 40 ° N y la longitud es de 83 ° W, lo que significa que Columbus está a 40 ° al norte del ecuador. Imagine un rayo desde el centro de la Tierra a través de Columbus y un rayo desde el centro de la Tierra a través del ecuador directamente al sur de Columbus. La medida del ángulo formado por los rayos es de 40 °. Del mismo modo, midiendo desde el primer meridiano, Columbus se encuentra a 83 ° hacia el oeste. Exprese la ubicación de Columbus en coordenadas esféricas.

Solución:
El radio de la Tierra es de 4000 mi, entonces ρ = 4000. La intersección del meridiano principal y el ecuador se encuentra en el eje x positivo. Luego, el movimiento hacia el oeste se describe con medidas de ángulo negativo, lo que muestra que θ = −83 °, ya que Columbus se encuentra a 40 ° al norte del ecuador, se encuentra a 50 ° al sur del Polo Norte, por lo que φ = 50 °. En coordenadas esféricas, Columbus se encuentra en el punto (4000, −83 °, 50 °).

Ejercicio de control 10.7.6

Sídney, Australia está en 34°S y 151°E. Expresa la ubicación de Sydney en coordenadas esféricas. ♦

Las coordenadas cilíndricas y esféricas nos dan la flexibilidad de seleccionar un sistema de coordenadas apropiado para el problema en cuestión. Una elección cuidadosa del sistema de coordenadas puede hacer que un problema sea mucho más fácil de resolver, mientras que una mala elección puede conducir a cálculos innecesariamente complejos. En el siguiente ejemplo, examinamos varios problemas diferentes y discutimos cómo seleccionar el mejor sistema de coordenadas para cada uno.

EJEMPLO ILUSTRATIVO 10.7_8 Elegir el mejor sistema de coordenadas

En cada una de las siguientes situaciones, determinamos qué sistema de coordenadas es el más apropiado y describimos cómo orientaríamos los ejes de coordenadas. Podría haber más de una respuesta correcta sobre cómo deberían orientarse los ejes, pero seleccionamos una orientación que tenga sentido en el contexto del problema. Nota: No hay suficiente información para configurar o resolver estos problemas; simplemente seleccionamos el sistema de coordenadas (Figura 10.7_17).
a. Encuentra el centro de gravedad de una bola de boliche.
b. Determine la velocidad de un submarino sometido a una corriente oceánica.
c. Calcule la presión en un tanque de agua cónico.
d. Encuentre el volumen de petróleo que fluye a través de una tubería.
e. Determine la cantidad de cuero requerida para hacer una pelota de fútbol.

Solución:
a. Claramente, una bola de boliche es una esfera, por lo que las coordenadas esféricas probablemente funcionarían mejor aquí. El origen debe estar ubicado en el centro físico de la pelota. No hay una opción obvia de cómo deben orientarse los ejes x, y y z. Las bolas de boliche normalmente tienen un bloque de peso en el centro. Una opción posible es alinear el eje z con el eje de simetría del bloque de peso.
b. Un submarino generalmente se mueve en línea recta. No hay simetría rotacional o esférica que se aplique en esta situación, por lo que las coordenadas rectangulares son una buena opción. El eje z probablemente debería apuntar hacia arriba. Los ejes x e y podrían alinearse para apuntar al este y al norte, respectivamente. El origen debe ser una ubicación física conveniente, como la posición inicial del submarino o la ubicación de un puerto en particular.
c. Un cono tiene varios tipos de simetría. En coordenadas cilíndricas, un cono puede ser representado por la ecuación z = kr, donde k es una constante. En coordenadas esféricas, hemos visto que las superficies de la forma φ = c son semiconos. Por último, en coordenadas rectangulares, los conos elípticos son superficies cuadráticas y se pueden representar mediante ecuaciones de la forma z² = x²/a² + y²/b². En este caso, podríamos elegir cualquiera de los tres. Sin embargo, la ecuación para la superficie es más complicada en coordenadas rectangulares que en los otros dos sistemas, por lo que es posible que deseemos evitar esa elección. Además, estamos hablando de un tanque de agua, y la profundidad del agua podría entrar en juego en algún momento de nuestros cálculos, por lo que podría ser bueno tener un componente que represente la altura y la profundidad directamente. Según este razonamiento, las coordenadas cilíndricas podrían ser la mejor opción. Elija el eje z para alinear con el eje del cono. La orientación de los otros dos ejes es arbitraria. El origen debe ser el punto inferior del cono.
d. Una tubería es un cilindro, por lo que las coordenadas cilíndricas serían la mejor opción. En este caso, sin embargo, probablemente optaríamos por orientar nuestro eje z con el eje central de la tubería. El eje x podría elegirse para apuntar hacia abajo o hacia alguna otra dirección lógica. El origen debe elegirse en función del enunciado del problema. Tenga en cuenta que esto pone el eje z en una orientación horizontal, que es un poco diferente de lo que solemos hacer. Puede tener sentido elegir una orientación inusual para los ejes si tiene sentido para el problema.
e. Una pelota de fútbol tiene simetría rotacional sobre un eje central, por lo que las coordenadas cilíndricas funcionarían mejor. El eje z debe alinearse con el eje de la pelota. El origen podría ser el centro de la pelota o quizás uno de los extremos. La posición del eje x es arbitraria.

Ejercicio de control 10.7.7