| 10. Cálculo vectorial – Vectores en el espacio | 10.7 Coordenadas cilíndricas y esféricas |
Ejercicios resueltos para el Capítulo 10.7
Utiliza la figura siguiente como ayuda para identificar la relación entre los sistemas de coordenadas rectangulares, cilíndricas y esféricas.
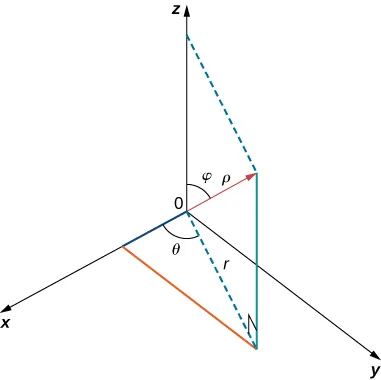
Para los siguientes ejercicios, se dan las coordenadas cilíndricas $(r, \theta, z)$ de un punto. Encuentre las coordenadas rectangulares $(x, y, z)$ del punto.
363. $\left( 4, \frac{\pi}{6}, 3 \right)$
364. $\left( 3, \frac{\pi}{3}, 5 \right)$
365. $\left( 4, \frac{7\pi}{6}, 3 \right)$
366. $( 2, \pi, -4 )$
Para los siguientes ejercicios, se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentre las coordenadas cilíndricas $(r, \theta, z)$ del punto.
367. $(1, \sqrt{3}, 2)$
368. $(1, 1, 5)$
369. $(3, -3, 7)$
370. $(-2\sqrt{2}, 2\sqrt{2}, 4)$
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas cilíndricas. Encuentre la ecuación de la superficie en coordenadas rectangulares. Identifique y grafique la superficie.
371. [T] $r = 4$
372. [T] $z = r^2\cos^2\theta$
373. [T] $r^2\cos(2\theta) + z^2 + 1 = 0$
374. [T] $r = 3 \sin \theta$
375. [T] $r = 2 \cos \theta$
376. [T] $r^2 + z^2 = 5$
377. [T] $r = 2 \sec \theta$
378. [T] $r = 3 \csc \theta$
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentre la ecuación de la superficie en coordenadas cilíndricas.
379. $z = 3$
380. $x = 6$
381. $x^2 + y^2 + z^2 = 9$
382. $y = 2x^2$
383. $x^2 + y^2 – 16x = 0$
384. $x^2 + y^2 – 3\sqrt{x^2 + y^2} + 2 = 0$
Para los siguientes ejercicios, se dan las coordenadas esféricas $(\rho, \theta, \varphi)$ de un punto. Encuentre las coordenadas rectangulares $(x, y, z)$ del punto.
385. $(3, 0, \pi)$
386. $\left(1, \frac{\pi}{6}, \frac{\pi}{6}\right)$
387. $\left(12, -\frac{\pi}{4}, \frac{\pi}{4}\right)$
388. $\left(3, \frac{\pi}{4}, \frac{\pi}{6}\right)$
Para los siguientes ejercicios, se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentre las coordenadas esféricas $(\rho, \theta, \varphi)$ del punto. Exprese la medida de los ángulos en grados redondeados al entero más cercano.
389. $(4, 0, 0)$
390. $(-1, 2, 1)$
391. $(0, 3, 0)$
392. $(-2, 2\sqrt{3}, 4)$
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas esféricas. Encuentre la ecuación de la superficie en coordenadas rectangulares. Identifique y grafique la superficie.
393. [T] $\rho = 3$
394. [T] $\varphi = \frac{\pi}{3}$
395. [T] $\rho = 2 \cos \varphi$
396. [T] $\rho = 4 \csc \varphi$
397. [T] $\varphi = \frac{\pi}{2}$
398. [T] $\rho = 6 \csc \varphi \sec \theta$
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentre la ecuación de la superficie en coordenadas esféricas. Identifique la superficie.
399. $x^2 + y^2 – 3z^2 = 0, z \neq 0$
400. $x^2 + y^2 + z^2 – 4z = 0$
401. $z = 6$
402. $x^2 + y^2 = 9$
Para los siguientes ejercicios, se dan las coordenadas cilíndricas de un punto. Encuentre sus coordenadas esféricas asociadas, con la medida del ángulo $\varphi$ en radianes redondeada a cuatro decimales.
403. [T] $\left(1, \frac{\pi}{4}, 3\right)$
404. [T] $(5, \pi, 12)$
405. $\left(3, \frac{\pi}{2}, 3\right)$
406. $\left(3, -\frac{\pi}{6}, 3\right)$
Para los siguientes ejercicios, se dan las coordenadas esféricas de un punto. Encuentre sus coordenadas cilíndricas asociadas.
407. $\left(2, -\frac{\pi}{4}, \frac{\pi}{2}\right)$
408. $\left(4, \frac{\pi}{4}, \frac{\pi}{6}\right)$
409. $\left(8, \frac{\pi}{3}, \frac{\pi}{2}\right)$
410. $\left(9, -\frac{\pi}{6}, \frac{\pi}{3}\right)$
Para los siguientes ejercicios, encuentre el sistema de coordenadas más adecuado para describir los sólidos dados.
411. El sólido situado en el primer octante con un vértice en el origen y encerrado por un cubo de arista de longitud $a$, donde $a > 0$.
412. Una cáscara esférica determinada por la región entre dos esferas concéntricas centradas en el origen, de radios $a$ y $b$, respectivamente, donde $b > a > 0$.
413. Un sólido dentro de la esfera $x^2 + y^2 + z^2 = 9$ y fuera del cilindro $(x – \frac{3}{2})^2 + y^2 = \frac{9}{4}$.
414. Una cáscara cilíndrica de altura 10 determinada por la región entre dos cilindros con el mismo centro, generatrices paralelas y radios de 2 y 5, respectivamente.
415. [T] Use un CAS para graficar la región entre el paraboloide elíptico $z = x^2 + y^2$ y el cono $x^2 + y^2 – z^2 = 0$. Luego describa la región en coordenadas cilíndricas.
416. [T] Use un CAS para graficar en coordenadas esféricas la región de “cono de helado” situada sobre el plano $xy$ entre la esfera $x^2 + y^2 + z^2 = 4$ y el cono elíptico $x^2 + y^2 – z^2 = 0$.
417. Washington, DC, se encuentra a $39^\circ$ N y $77^\circ$ W. Suponga que el radio de la Tierra es de 4000 mi. Exprese la ubicación de Washington, DC, en coordenadas esféricas.
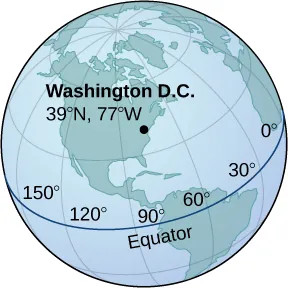
418. San Francisco se encuentra a $37.78^\circ$ N y $122.42^\circ$ W. Suponga que el radio de la Tierra es de $4000$ mi. Exprese la ubicación de San Francisco en coordenadas esféricas.
419. Encuentre la latitud y longitud de Río de Janeiro si sus coordenadas esféricas son $(4000, -43.17^\circ, 102.91^\circ)$.
420. Encuentre la latitud y longitud de Berlín si sus coordenadas esféricas son $(4000, 13.38^\circ, 37.48^\circ)$.
421. [T] Considere el toro de ecuación $(x^2 + y^2 + z^2 + R^2 – r^2)^2 = 4R^2(x^2 + y^2)$, donde $R \geq r > 0$.
a. Escriba la ecuación del toro en coordenadas esféricas.
b. Si $R = r$, la superficie se llama toro de cuerno. Demuestre que la ecuación de un toro de cuerno en coordenadas esféricas es $\rho = 2R \sin \varphi$.
c. Use un CAS para graficar el toro de cuerno con $R = r = 2$ en coordenadas esféricas.
422. [T] La “esfera rugosa” con una ecuación en coordenadas esféricas $\rho = a + b \cos(m\theta)\sin(n\varphi)$, con $\theta \in [0, 2\pi]$ y $\varphi \in [0, \pi]$, donde $a$ y $b$ son números positivos y $m$ y $n$ son enteros positivos, puede usarse en matemática aplicada para modelar el crecimiento de tumores.
a. Demuestre que la “esfera rugosa” está contenida dentro de una esfera de ecuación $\rho = a + b$. Encuentre los valores de $\theta$ y $\varphi$ en los que las dos superficies se intersecan.
b. Use un CAS para graficar la superficie para $a = 14, b = 2, m = 4$ y $n = 6$ junto con la esfera $\rho = a + b$.
c. Encuentre la ecuación de la curva de intersección de la superficie en b. con el cono $\varphi = \frac{\pi}{12}$. Grafique la curva de intersección en el plano de intersección.
una ayuda por favor : ojo B =11
Se A un punto en el espacio que en coordenadas cartesianas está dado por la posición Bi + (B+3)j + 4k,
sobre esta posición se construye el vector C = 2i + 4j – 5k.
a) Muestre el vector C en coordenadas cilíndricas.
b) Muestre el vector C en coordenadas esféricas.
What’s up colleagues, how is everything, and
what you would like to say on the topic of this
piece of writing, in my view its truly awesome in support of me.
Great content! Super high-quality! Keep it up! 🙂