| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.4 |
10.4 EL PRODUCTO CRUZ: Objetivos de aprendizaje
10.4.1 Calcule el producto cruz de dos vectores dados.
10.4.2 Usa determinantes para calcular un producto cruz.
10.4.3 Encuentre un vector ortogonal a dos vectores dados.
10.4.4 Determine áreas y volúmenes utilizando el producto cruz.
10.4.5 Calcule el torque dada la fuerza y el vector de posición.
Imagina un mecánico que gira una llave para apretar un tornillo. El mecánico aplica una fuerza en el extremo de la llave. Esto crea una rotación, o torque, que aprieta el tornillo. Podemos usar vectores para representar la fuerza aplicada por el mecánico y la distancia (radio) desde el tornillo hasta el extremo de la llave. Luego, podemos representar el torque mediante un vector orientado a lo largo del eje de rotación. Observa que el vector de torque es ortogonal tanto al vector de fuerza como al vector de radio.
En esta sección, desarrollamos una operación llamada producto cruz, que nos permite encontrar un vector ortogonal a dos vectores dados. Calcular el torque es una aplicación importante del producto cruz, y examinaremos el torque con más detalle más adelante en la sección.

El producto cruz y sus propiedades
El producto punto es una multiplicación de dos vectores que da como resultado un escalar. En esta sección, presentamos un producto de dos vectores que genera un tercer vector ortogonal a los dos primeros. Considere cómo podríamos encontrar ese vector. Deje que u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ sean vectores distintos de cero. Queremos encontrar un vector w = ⟨w₁, w₂, w₃⟩ ortogonal a u y v, es decir, queremos encontrar w tal que u⋅w = 0 y v⋅w = 0. Por lo tanto, w₁, w₂ y w₃ deben satisfacer
u₁ w₁ + u₂ w₂ + u₃ w₃ = 0
v₁ w₁ + v₂ w₂ + v₃ w₃ = 0.
Si multiplicamos la ecuación superior por v₃ y la ecuación inferior por u₃ y restamos, podemos eliminar la variable w₃, esto es
(u₁ v₃ − v₁ u₃) w₁ + (u₂ v₃ − v₂ u₃) w₂ = 0.
Si seleccionamos
w₁ = u₂ v₃ − u₃ v₂
w₂ =− (u₁ v₃ − u₃ v₁),
obtenemos un posible vector solución. Sustituir estos valores nuevamente en las ecuaciones originales da
w₃ = u₁ v₂ − u₂ v₁.
Es decir, el vector
w = ⟨u₂ v₃ − u₃ v₂, − (u₁ v₃ − u₃ v₁), u₁ v₂ − u₂ v₁⟩
es ortogonal a u y v, lo que nos lleva a definir la siguiente operación, llamada producto cruz.
Definición. Producto cruz
Sean \(\mathbf{u} = \langle u_1, u_2, u_3 \rangle\) y \(\mathbf{v} = \langle v_1, v_2, v_3 \rangle\). Entonces, el producto vectorial \(\mathbf{u} \times \mathbf{v}\) es el vector
♦
Por la forma en que hemos desarrollado u × v, debe quedar claro que el producto cruz es ortogonal tanto para u como para v. Sin embargo, nunca está de más comprobarlo. Para mostrar que u × v es ortogonal a u, calculamos el producto escalar de u y u × v.

De manera similar, podemos mostrar que el producto cruza también es ortogonal a v.
EJEMPLO ILUSTRATIVO 10.4_1. Encontrar un producto cruz
Sea p = ⟨−1, 2, 5⟩ y q = ⟨4, 0, −3⟩ (Figura 10.4_1). Encuentra p × q.

Figura 10.4_1 Encontrar el producto cruz para dos vectores dados.
Solución:
Sustituya los componentes de los vectores en la ecuación del producto cruz:

Ejercicio de control 10.4.1
Encuentre \(\mathbf{p} \times \mathbf{q}\) para \(\mathbf{p} = \langle 5, 1, 2 \rangle\) y \(\mathbf{q} = \langle -2, 0, 1 \rangle\). Exprese la respuesta utilizando vectores unitarios estándar.
Aunque puede no ser obvio en la ecuación del producto cruz, la dirección de u × v viene dada por la regla de la derecha. Si levantamos la mano derecha con los dedos apuntando en la dirección de u, luego doblamos los dedos hacia el vector v, el pulgar apunta en la dirección del producto cruzo, como se muestra en la figura siguiente:

Observe lo que esto significa para la dirección de v × u. Si aplicamos la regla de la mano derecha a v × u, comenzamos con nuestros dedos apuntando en la dirección de v, luego doblamos nuestros dedos hacia el vector u. En este caso, el pulgar apunta en la dirección opuesta de u × v. (¡Intentalo!)
EJEMPLO ILUSTRATIVO 10.4_2. Anticonmutatividad del producto cruz
Sea u = ⟨0, 2, 1⟩ y v = ⟨3, −1, 0⟩. Calcule u × v y v × u y grafíquelos.

Solución:
Tenemos

Vemos que, en este caso, u × v = – (v × u) (Figura 10.4_4). Probamos esto en general más adelante en esta sección.

Ejercicio de control 10.4.2
Supongamos que los vectores u y v se encuentran en el plano xy (la componente z de cada vector es cero). Ahora supongamos que las componentes x e y de u y la componente y de v son todas positivas, mientras que la componente x de v es negativa. Asumiendo que los ejes coordenados están orientados en las posiciones habituales, ¿en qué dirección apunta u × v?
Los productos cruz de los vectores unitarios estándar i, j y k pueden ser útiles para simplificar algunos cálculos, así que consideremos estos productos cruz. Una aplicación directa de la definición muestra que
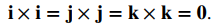
Además, debido a que el producto cruz de dos vectores es ortogonal a cada uno de estos vectores, sabemos que el producto cruz de i y j es paralelo a k. Del mismo modo, el producto vectorial de i y k es paralelo a j, y el producto vectorial de j y k es paralelo a i. Podemos usar la regla de la mano derecha para determinar la dirección de cada producto. Entonces tenemos

Estas fórmulas son útiles más tarde.
EJEMPLO ILUSTRATIVO 10.4_3. Producto cruz de vectores de unidad estándar
Encuentre i × (j × k).
Solución:
Sabemos que j × k = i. Por lo tanto, i × (j × k) = i × i = 0.
Ejercicio de control 10.4.3
Halle (𝐢 × 𝐣) × (𝐤 × 𝐢).
Como hemos visto, el producto punto a menudo se llama producto escalar porque da como resultado un escalar. El producto cruz da como resultado un vector, por lo que a veces se denomina producto vectorial. Estas operaciones son versiones de multiplicación de vectores, pero tienen propiedades y aplicaciones muy diferentes. Exploremos algunas propiedades del producto cruz. Probamos solo algunas de ellas. Las pruebas de las otras propiedades se dejan como ejercicios.
TEOREMA 10.4_1. Propiedades del producto cruzSupongamos que u, v y w son vectores en el espacio, y que c sea n escalar.
|
Prueba:
Para la propiedad i., Queremos mostrar u × v = – (v × u). Tenemos
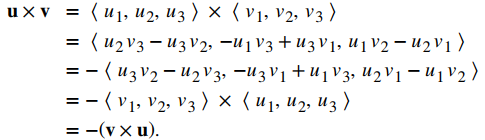
A diferencia de la mayoría de las operaciones que hemos visto, el producto cruz no es conmutativo. Esto tiene sentido si pensamos en la regla de la mano derecha.
Para la propiedad iv., Esto se deduce directamente de la definición del producto cruz. Tenemos
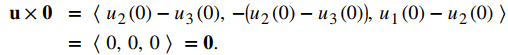
Entonces, por propiedad i., 0 × u = 0 también. Recuerde que el producto escalar de un vector y el vector cero es el escalar 0, mientras que el producto cruz de un vector con el vector cero es el vector 0.
Propiedad vi. se parece a la propiedad asociativa, pero tenga en cuenta el cambio en las operaciones:
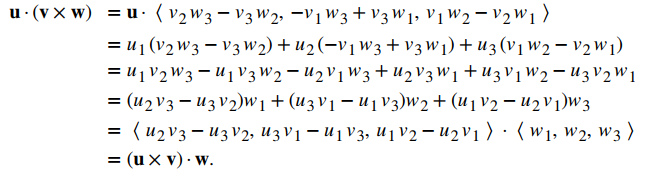
EJEMPLO ILUSTRATIVO 10.4_4. Uso de las propiedades del producto cruz
Use las propiedades del producto cruzado para calcular (2i × 3j) × j.
Solución:

Ejercicio de control 10.4.4
Halle (𝐢 × k) × (𝐤 × j).
Hasta ahora en esta sección, nos hemos preocupado por la dirección del vector u × v, pero no hemos discutido su magnitud. Resulta que hay una expresión simple para la magnitud de u × v que involucra las magnitudes de u y v, y el seno del ángulo entre ellos.
TEOREMA 10.4_2. Magnitud del producto cruz
Sean u y v vectores, y sea θ el ángulo entre ellos. Entonces,
∥u × v∥ = ∥u∥⋅∥v∥⋅senθ. ♦
Prueba:Sean u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ vectores, y sea θ el ángulo entre ellos. Luego
Tomando raíces cuadradas y notando que
obtenemos el resultado deseado:
|
Esta definición del producto cruz nos permite visualizar o interpretar el producto geométricamente. Está claro, por ejemplo, que el producto cruz se define solo para vectores en tres dimensiones, no para vectores en dos dimensiones. En dos dimensiones, es imposible generar un vector simultáneamente ortogonal a dos vectores no paralelos.
EJEMPLO ILUSTRATIVO 10.4_5. Cálculo del producto cruz
Use las propiedades del producto cruzo para encontrar la magnitud del producto cruz de u = ⟨0,4,0⟩ y v = ⟨0,0, −3⟩.
Solución:
Tenemos
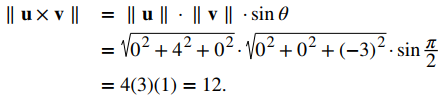
Ejercicio de control 10.4.5
Utilizar las propiedades del producto vectorial para determinar la magnitud de 𝐮 × 𝐯, donde 𝐮 = 〈−8, 0, 0〉 y 𝐯 = 〈0, 2, 0〉.
Determinantes y el producto cruz
Usar la ecuación dada en la definición del producto cruz para encontrar el producto cruz de dos vectores es sencillo y presenta el producto cruz en la forma de componente útil. La fórmula, sin embargo, es complicada y difícil de recordar. Afortunadamente, tenemos una alternativa. Podemos calcular el producto cruz de dos vectores usando notación de determinante.
♦ Un determinante 2 × 2 se define por
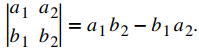
Por ejemplo

♦ El determinante 3 × 3 se define en términos de determinantes 2 × 2 de la siguiente manera:
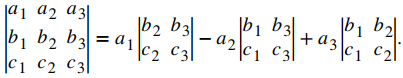
La ecuación anterior se conoce como la expansión del determinante a lo largo de la primera fila. Observe que los multiplicadores de cada uno de los determinantes 2 × 2 en el lado derecho de esta expresión son las entradas en la primera fila del determinante 3 × 3. Además, cada uno de los determinantes 2 × 2 contiene las entradas del determinante 3 × 3 que quedarían si tachara la fila y la columna que contiene el multiplicador. Por lo tanto, para el primer término a la derecha, a₁ es el multiplicador, y el determinante 2 × 2 contiene las entradas que quedan si tacha la primera fila y la primera columna del determinante 3 × 3. Del mismo modo, para el segundo término, el multiplicador es a₂, y el determinante 2 × 2 contiene las entradas que quedan si tacha la primera fila y la segunda columna del determinante 3 × 3. Observe, sin embargo, que el coeficiente del segundo término es negativo. El tercer término se puede calcular de manera similar.
EJEMPLO ILUSTRATIVO 10.4_6. Uso de la expansión a lo largo de la primera fila para calcular un determinante 3 × 3
Evaluar el determinante
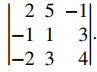
Tenemos
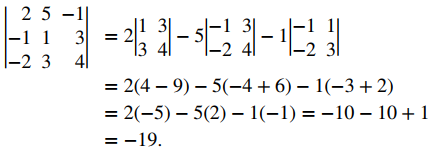
Ejercicio de control 10.4.6
Evalúe el determinante $$ \begin{vmatrix} 1 & -2 & -1 \\ 3 & 2 & -3 \\ 1 & 5 & 4 \end{vmatrix}. $$
Técnicamente, los determinantes se definen sólo en términos de matrices de números reales. Sin embargo, la notación de determinante proporciona un dispositivo mnemónico útil para la fórmula del producto cruz.
REGLA: PRODUCTO CRUZ CALCULADO POR UN DETERMINANTE
Sean $\mathbf{u} = \langle u_1, u_2, u_3 \rangle$ y $\mathbf{v} = \langle v_1, v_2, v_3 \rangle$ vectores. Entonces el producto cruz $\mathbf{u} \times \mathbf{v}$ está dado por
$$\mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix} = \begin{vmatrix} u_2 & u_3 \\ v_2 & v_3 \end{vmatrix} \mathbf{i} – \begin{vmatrix} u_1 & u_3 \\ v_1 & v_3 \end{vmatrix} \mathbf{j} + \begin{vmatrix} u_1 & u_2 \\ v_1 & v_2 \end{vmatrix} \mathbf{k}$$EJEMPLO ILUSTRATIVO 10.4_7. Usando la notación de determinante para encontrar p × q
Sean p = ⟨− 1, 2, 5⟩ y q = ⟨4, 0, −3⟩. Encuentra p × q.
Solución:
Configuramos nuestro determinante colocando los vectores unitarios estándar en la primera fila, los componentes de u en la segunda fila y los componentes de v en la tercera fila. Entonces tenemos

Ejercicio de control 10.4.7
Use la notación de determinante para encontrar $\mathbf{a} \times \mathbf{b}$, donde $\mathbf{a} = \langle 8, 2, 3 \rangle$ y $\mathbf{b} = \langle -1, 0, 4 \rangle$.
Usando el producto cruz
El producto cruza es muy útil para varios tipos de cálculos, que incluyen encontrar un vector ortogonal a dos vectores dados, calcular áreas de triángulos y paralelogramos, e incluso determinar el volumen de la forma geométrica tridimensional hecha de paralelogramos conocidos como paralelepípedos.
EJEMPLO ILUSTRATIVO 10.4_8. Encontrar un vector unitario ortogonal a dos vectores dados
Sea a = ⟨5, 2, −1⟩ y b = ⟨0, −1, 4⟩. Encuentre un vector unitario ortogonal a a y b.
Solución:
El producto cruz a × b es ortogonal a ambos vectores a y b. Podemos calcularlo con un determinante:

Normalice este vector para encontrar un vector unitario en la misma dirección:
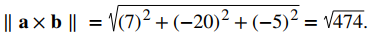
Así,

es un vector unitario ortogonal a a y b.
Ejercicio de control 10.4.8
Encuentre un vector unitario ortogonal tanto a $\mathbf{a}$ como a $\mathbf{b}$, donde $\mathbf{a} = \langle 4, 0, 3 \rangle$ y $\mathbf{b} = \langle 1, 1, 4 \rangle$.
Para usar el producto cruz para calcular áreas, establecemos y probamos el siguiente teorema.
TEOREMA 10.4_3. Área de un paralelogramo
Si ubicamos los vectores u y v de manera que formen lados adyacentes de un paralelogramo, entonces el área del paralelogramo viene dada por ∥u × v∥ (Figura 10.4_5).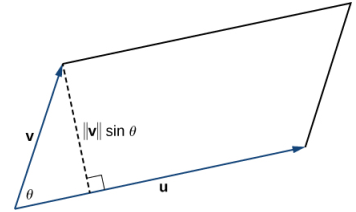
(Figura 10.4_5 El paralelogramo con lados adyacentes u y v tiene una base ∥u∥ y una altura ∥v∥senθ.)
Prueba:
Mostramos que la magnitud del producto cruz es igual a la base por la altura del paralelogramo.
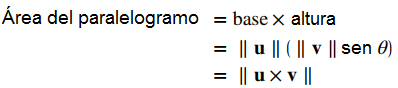
EJEMPLO ILUSTRATIVO 10.4_9. Encontrar el área de un triángulo
Sean P = (1, 0, 0), Q = (0, 1, 0) y R = (0, 0, 1) los vértices de un triángulo (Figura 10.4_6). Encuentra su área.

Solución:
Tenemos
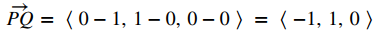
y
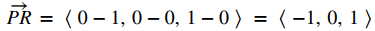
El área del paralelogramo con lados adyacentes
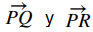
está dado por


El área de ΔPQR es la mitad del área del paralelogramo, o √3 / 2.
Ejercicio de control 10.4.9
Encuentre el área del paralelogramo $PQRS$ con vértices $P(1, 1, 0)$, $Q(7, 1, 0)$, $R(9, 4, 2)$ y $S(3, 4, 2)$.
El producto escalar triple
Debido a que el producto cruz de dos vectores es un vector, es posible combinar el producto escalar y el producto cruz. El producto escalar de un vector con el producto cruz de otros dos vectores se llama producto escalar triple porque el resultado es un escalar.
DEFINICIÓN. Producto escalar triple
El producto escalar triple de los vectores u, v y w es
u⋅ (v × w).
TEOREMA 10.4_4. Cálculo de un producto triple escalar
El producto escalar triple de los vectores u = u₁i + u₂j + u₃k, v = v₁i + v₂j + v₃k, y w = w₁i + w₂j + w₃k es el determinante de la matriz 3 × 3 formada por los componentes de los vectores:
Prueba:El cálculo es sencillo.
|
EJEMPLO ILUSTRATIVO 10.4_10. Cálculo del producto escalar triple
Sea u = ⟨1, 3, 5⟩, v = ⟨2, −1, 0⟩ y w = ⟨− 3, 0, −1⟩. Calcule el producto escalar triple u⋅ (v × w).
Solución:
Aplicar el cálculo de un producto escalar triple directamente:
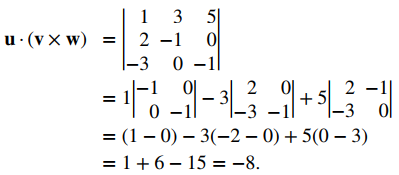
Ejercicio de control 10.4.10
Calcule el triple producto escalar $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$, donde $\mathbf{a} = \langle 2, -4, 1 \rangle$, $\mathbf{b} = \langle 0, 3, -1 \rangle$ y $\mathbf{c} = \langle 5, -3, 3 \rangle$.
Cuando creamos una matriz a partir de tres vectores, debemos tener cuidado con el orden en que enumeramos los vectores. Si los enumeramos en una matriz en un orden y luego reorganizamos las filas, el valor absoluto del determinante permanece sin cambios. Sin embargo, cada vez que dos filas cambian de lugar, el determinante cambia de signo:

Verificar este hecho es sencillo, pero bastante engorroso. Echemos un vistazo a esto con un ejemplo:
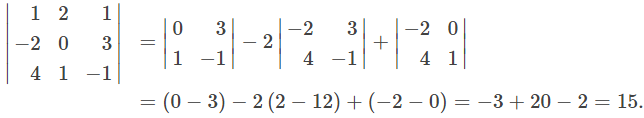
Cambiando las dos filas superiores obtenemos
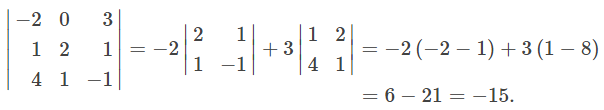
Reorganizar los vectores en los productos triples es equivalente a reordenar las filas en la matriz del determinante. Sea u = u = u₁i + u₂j + u₃k, v = v₁i + v₂j + v₃k, y w = w₁i + w₂j + w₃k. Aplicando el cálculo de un producto escalar triple, tenemos
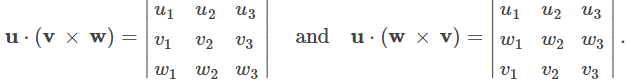
Podemos obtener el determinante para calcular u⋅ (w × v) cambiando las dos filas inferiores de u⋅ (v × w). Por lo tanto, u⋅ (v × w) = – u⋅ (w × v).
Siguiendo este razonamiento y explorando las diferentes formas en que podemos intercambiar variables en el producto triple escalar, se obtienen las siguientes identidades:
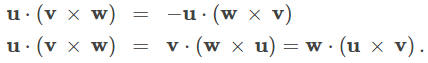
Sean u y v dos vectores en posición estándar. Si u y v no son múltiplos escalares entre sí, entonces estos vectores forman lados adyacentes de un paralelogramo. Vimos en el Área de un paralelogramo que el área de este paralelogramo es ∥u × v∥. Ahora supongamos que agregamos un tercer vector w que no se encuentra en el mismo plano que u y v pero que aún comparte el mismo punto inicial. Luego, estos vectores forman tres lados de un paralelepípedo, un prisma tridimensional con seis caras que son cada uno paralelogramos, como se muestra en la Figura 10.4_7. El volumen de este prisma es el producto de la altura y el área de su base. El producto escalar triple de u, v y w proporciona un método simple para calcular el volumen del paralelepípedo definido por estos vectores.
TEOREMA 10.4_5. Volumen de un paralelepípedo
El volumen de un paralelepípedo con bordes adyacentes dados por los vectores u, v, y w es el valor absoluto del producto escalar triple:
V = | u⋅ (v × w) |.
Ver figura 10.4_7
Tenga en cuenta que, como su nombre lo indica, el producto escalar triple produce un escalar. La fórmula de volumen que se acaba de presentar utiliza el valor absoluto de una cantidad escalar.
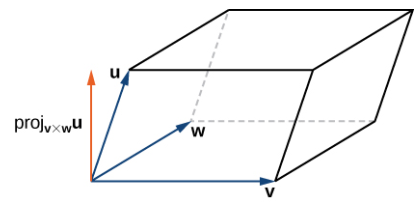
Prueba:El área de la base del paralelepípedo viene dada por ∥v × w∥. La altura de la figura viene dada por ∥projv × wu∥. El volumen del paralelepípedo es el producto de la altura y el área de la base, por lo que tenemos
|
EJEMPLO ILUSTRATIVO 10.4_11. Cálculo del volumen de un paralelepípedo
Sea u = ⟨− 1, −2, 1⟩, v = ⟨4, 3,2 ⟩ y w = ⟨0, −5, −2⟩. Encuentre el volumen del paralelepípedo con bordes adyacentes u, v y w (Figura 10.4_8).

Solución:
Tenemos

Por lo tanto, el volumen del paralelepípedo es | −40 | = 40 unidades³.
Ejercicio de control 10.4.11
Encuentre el volumen del paralelepípedo formado por los vectores $\mathbf{a} = 3\mathbf{i} + 4\mathbf{j} – \mathbf{k}$, $\mathbf{b} = 2\mathbf{i} – \mathbf{j} – \mathbf{k}$ y $\mathbf{c} = 3\mathbf{j} + \mathbf{k}$.
Aplicaciones del producto cruz
El producto cruza aparece en muchas aplicaciones prácticas en matemáticas, física e ingeniería. Examinemos algunas de estas aplicaciones aquí, incluida la idea del torque, con el que comenzamos esta sección. Otras aplicaciones aparecen en capítulos posteriores, particularmente en nuestro estudio de campos vectoriales como los campos gravitacionales y electromagnéticos (Introducción al cálculo vectorial).
Ejercicio de control 10.4.12
¿Son coplanares los vectores $\mathbf{a} = \mathbf{i} + \mathbf{j} – \mathbf{k}$, $\mathbf{b} = \mathbf{i} – \mathbf{j} + \mathbf{k}$ y $\mathbf{c} = \mathbf{i} + \mathbf{j} + \mathbf{k}$?
EJEMPLO ILUSTRATIVO 10.4_12. Uso del producto escalar triple
Use el producto escalar triple para mostrar que los vectores u = ⟨2, 0, 5⟩, v = ⟨2, 2, 4⟩ y w = ⟨1, −1, 3⟩ son coplanares, es decir, demuestre que estos vectores se encuentran en el mismo plano.
Solución:
Comience calculando el producto escalar triple para encontrar el volumen del paralelepípedo definido por u, v, y w:
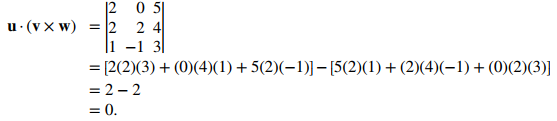
El volumen del paralelepípedo es de 0 unidades³, por lo que una de las dimensiones debe ser cero. Por lo tanto, los tres vectores se encuentran en el mismo plano.
EJEMPLO ILUSTRATIVO 10.4_13. Encontrar un vector ortogonal
Únicamente un solo plano puede pasar a través de cualquier conjunto de tres puntos no colineales. Encuentre un vector ortogonal al plano que contenga los puntos P = (9, −3, −2), Q = (1, 3, 0) y R = (- 2, 5, 0).
Solución:
El plano debe contener los vectores
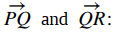
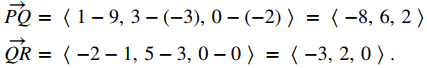
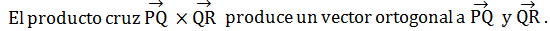
Por lo tanto, el producto cruz es ortogonal al plano que contiene estos dos vectores:
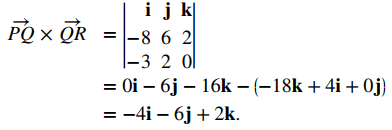
Hemos visto cómo usar el producto escalar triple y cómo encontrar un vector ortogonal a un plano. Ahora aplicamos el producto cruz a situaciones del mundo real.
Algunas veces una fuerza hace que un objeto gire. Por ejemplo, girar un destornillador o una llave crea este tipo de efecto de rotación, llamado torque.
DEFINICIÓN. Torque
Torque, τ (la letra griega tau), mide la tendencia de una fuerza a producir rotación alrededor de un eje de rotación. Sea r un vector con un punto inicial ubicado en el eje de rotación y con un punto terminal ubicado en el punto donde se aplica la fuerza, y deje que el vector F represente la fuerza. Entonces el torque es igual al producto cruzado de r y F:
τ = r × F.
Ver Figura 10.4_9.
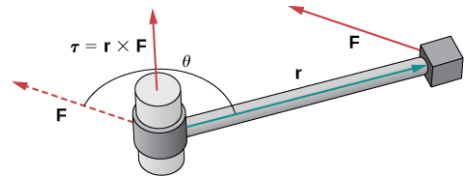
Piense en usar una llave para apretar un tornillo. El torque τ aplicado al perno depende de cuán fuerte empujemos la llave (fuerza) y cuán lejos del mango apliquemos la fuerza (distancia). El torque aumenta con una mayor fuerza sobre la llave a una mayor distancia del perno. Las unidades comunes de torque son el newton-metro o pie-libra. Aunque el torque es dimensionalmente equivalente al trabajo (tiene las mismas unidades), los dos conceptos son distintos. El torque se usa específicamente en el contexto de rotación, mientras que el trabajo generalmente implica movimiento a lo largo de una línea recta.
EJEMPLO ILUSTRATIVO 10.4_14. Evaluando el torque
Se aprieta un perno aplicando una fuerza de 6 N a una llave de 0,15 m (Figura 10.4_10). El ángulo entre la llave y el vector de fuerza es de 40°. Encuentre la magnitud del torque sobre el centro del perno. Redondea la respuesta a dos decimales.
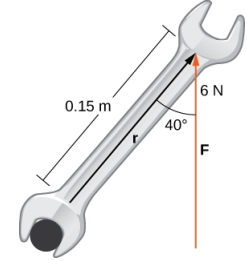
Solución:
Sustituya la información dada en la ecuación que define el torque:
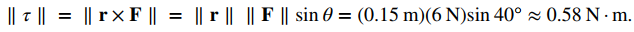
Ejercicio de control 10.4.13
Calcule la fuerza requerida para producir un torque de $15 \text{ N} \cdot \text{m}$ a un ángulo de $30^\circ$ desde una varilla de $150 \text{ cm}$.


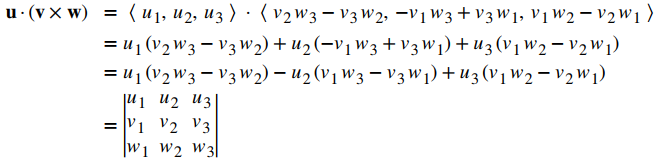
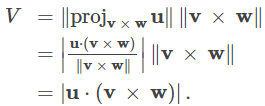
Hey there. I found your website via Google at the same time as searching for a related matter, your web site came up. It seems to be good. I have bookmarked it in my google bookmarks to visit then.
Great content! Super high-quality! Keep it up! 🙂