| 9. Ecuaciones diferenciales | 9.9. Ecuaciones lineales de orden superior | Ejercicios propuestos para el Capítulo 9.9.2 |

9.9.2  Ecuaciones homogéneas de coeficientes constantes de orden superior

Si a₀, a₁, . . . , a_n son constantes y a₀ ≠ 0, entonces

a₀y⁽ⁿ⁾ + a₁y^{(n − 1)} + · · · + a_ny = F(x)

se dice que es una se dice que es una ecuación de coeficientes constantes. En esta sección consideramos la ecuación de coeficientes constantes homogénea

a₀y⁽ⁿ⁾ + a₁y^{(n − 1)} + · · · + a_ny = 0        (9.9.2.1)

Dado que (9.9.2.1) es normal en (−∞, ∞), todos los teoremas de la Sección 9.9.1 se aplican con (a, b) = (−∞, ∞).

      Como en la Sección 9.5.2, llamamos

p(r) = a₀rⁿ + a₁r^{n − 1} + · · · + a_n         (9.9.2.2)

el polinomio característico de (9.9.2.1). Vimos en la Sección 9.5.2 que cuando n = 2 las soluciones de (9.9.2.1) están determinadas por los ceros del polinomio característico. Esto también es cierto cuando n > 2, pero la situación es más complicada en este caso. En consecuencia, adoptamos un enfoque diferente aquí que en la Sección 9.5.2.

Si k es un entero positivo, sea D^k el k-ésimo operador derivador; esto es

D^ky = y^(k).

Si

q(r) = b₀r^m + b₁r^{m − 1} + · · · + b_m

      Si k es un entero positivo, sea D^k el k-ésimo operador derivador; esto es

D^ky = y^(k).

Si

q(r) = b₀r^m + b₁r^{m − 1} + · · · + b_m

es un polinomio arbitrario, defina el operador

q(D) = b₀D^m + b₁D^{m − 1} + · · · + b_m

tal que

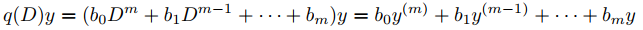
siempre que y sea una función con m derivadas. Llamamos a q(D) un operador polinomial.

      Con p como en (9.9.2.2),

p(D) = a₀Dⁿ + a₁D^{n − 1} + · · · + a_n,

entonces (9.9.2.1) se puede escribir como p(D)y = 0. Si r es una constante entonces

esto es

p(D)(e^rx) = p(r)e^rx.

Esto muestra que y = e^rx es una solución de (9.9.2.1) si p(r) = 0. En el caso más simple, donde p tiene n ceros reales distintos r₁, r₂,. . . , r_n, este argumento produce n soluciones

y₁ = e^r₁x,   y₂ = e^r₂x, . . .,   y_n = e^r_nx.

Se puede demostrar (Ejercicio 39) que el Wronskiano de {e^r₁x, e^r₂x, . . ., e^r_nx} es distinto de cero si r₁, r₂, . . . , r_n son distintos; por lo tanto, {e^r₁x, e^r₂x, . . ., e^r_nx} es un conjunto fundamental de soluciones de p(D)y = 0 en este caso.

Ejemplo ilustrativo 9.9.2.1

(a) Encuentre la solución general de

y′′′ − 6y′′ + 11y′ − 6y = 0.        (9.9.2.3)

(b) Resuelva el problema de valor inicial

y′′′ − 6y′′ + 11y′ − 6y = 0,  y(0) = 4,  y′(0) = 5,  y′′(0) = 9.        (9.9.2.4)

Solución:

(a) El polinomio característico de (9.9.2.3) es

p(r) = r³ − 6r² + 11r − 6 = (r − 1)(r − 2)(r − 3).

Por tanto {e^x, e^2x, e^3x} es un conjunto de soluciones de (9.9.2.3). Es un conjunto fundamental, ya que su Wronskiano es

Por tanto la solución general de (9.9.2.3) es

y = c₁e^x + c₂e^2x + c₃e^3x.        (9.9.2.5)

(b) Debemos determinar c₁, c₂ y c₃ en (9.9.2.5) para que y satisfaga las condiciones iniciales en (9.9.2.4). Diferenciar (9.9.2.5) dos veces produce

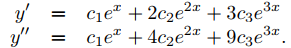        (9.9.2.6)

Estableciendo x = 0 en (9.9.2.5) y (9.9.2.6) e imponiendo las condiciones iniciales se obtiene

La solución de este sistema es c₁ = 4, c₂ = −1, c₃ = 1. Por lo tanto la solución de (9.9.2.4) es

y = 4e^x − e^2x + e^3x

Figura 9.9.2.1 y = 4e^x − e^2x + e^3x ♦

        Consideremos ahora el caso en el que el polinomio característico (9.9.2.2) no tiene n ceros reales distintos. Para ello es útil definir qué entendemos por factorización de un operador polinómial.
Comenzamos con un ejemplo.

Ejemplo ilustrativo 9.9.2.2

Considere el polinomio

p(r) = r³ − r² + r − 1

y el operador polinomial asociado

p(D) = D³ − D² + D − 1.

Dado que p(r) puede factorizarse como

p(r) = (r − 1)(r² + 1) = (r² + 1)(r − 1),

es razonable esperar que p(D) pueda factorizarse como

p(D) = (D − 1)(D² + 1) = (D² + 1)(D − 1).         (9.9.2.7)

Sin embargo, antes de que podamos hacer esta afirmación debemos definir qué queremos decir con que dos operadores son iguales y qué queremos decir con los productos de los operadores en (9.9.2.7). Decimos que dos operadores son iguales si se aplican a las mismas funciones y siempre producen el mismo resultado. La definición de los productos en (9.9.2.7) es la siguiente: si y es una función cualquiera tres veces diferenciable, entonces

(a) (D − 1)(D² + 1)y es la función obtenida aplicando primero D² + 1 a y y luego aplicando D − 1 a la función resultante

(b) (D − 1)(D² + 1)y es la función obtenida aplicando primero D − 1 a y y luego aplicando D² + 1 a la función resultante.

A partir de (a),

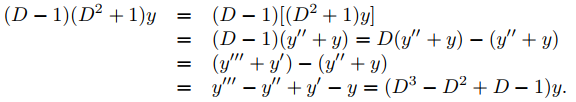      (9.9.2.8)

Esto implica que

(D − 1)(D² + 1) = (D³ − D² + D − 1).

De (b)

      (9.9.2.9)

(D² + 1)(D − 1) = (D³ − D² + D − 1),

lo que completa la justificación de (9.9.2.7). ♦

Ejemplo ilustrativo 9.9.2.3

Utilice el resultado del Ejemplo 9.9.2.2 para encontrar la solución general de

y′′′ − y′′ + y′ − y = 0.        (9.9.2.10)

Solución:

De (9.9.2.8), podemos reescribir (9.9.2.10) como

(D − 1)(D² + 1)y = 0,

lo que implica que cualquier solución de (D² + 1)y = 0 es una solución de (9.9.2.10). Por lo tanto y₁ = cosx e y₂ = senx son soluciones de (9.9.2.10).

      De (9.9.2.9), podemos reescribir (9.9.2.10) como

(D² + 1)(D − 1)y = 0,

lo que implica que cualquier solución de (D − 1)y = 0 es una solución de (9.9.2.10). Por lo tanto y₃ = e^x es la solución de (9.9.2.10).

        El wronskiano de {e^x, cosx, senx} es

Ya que

{cosx, senx, e^x} es linealmente independiente y

y = c₁cosx + c₂senx + c₃e^x

es la solución general de (9.9.2.10). ♦

Ejemplo ilustrativo 9.9.2.4

Encuentre la solución general de

y⁽⁴⁾ − 16y = 0.         (9.9.2.11)

Solución:

El polinomio característico de (9.9.2.11) es

p(r) = r⁴ − 16 = (r² − 4)(r² + 4) = (r − 2)(r + 2)(r² + 4).

Mediante argumentos similares a los utilizados en los ejemplos 9.9.2.2 y 9.2.3, se puede demostrar que (9.9.2.11) se puede escribir como

(D² + 4)(D + 2)(D − 2)y = 0

o

(D² + 4)(D − 2)(D + 2)y = 0

o

(D − 2)(D + 2)(D² + 4)y = 0.

Por lo tanto y es solución de (9.9.2.11) si es solución de cualquiera de las tres ecuaciones

(D − 2)y = 0,  (D + 2)y = 0,  (D² + 4)y = 0.

Por tanto, {e^2x, e^−2x, cos2x, sen2x} es un conjunto de soluciones de (9.9.2.11). El wronskiano de este conjunto es

Ya que

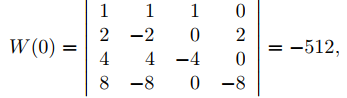
{e^2x, e^−2x, cos2x, sen2x} es linealmente independiente y

y₁ = c₁e^2x + c₂^2x + c₃cos2x + c₄sen2x

es la solución general de (9.9.2.11). ♦

      Se sabe por álgebra que todo polinomio

p(r) = a₀rⁿ + a₁r^{n − 1} + · · · + a_n

con coeficientes reales se puede factorizar como

p(r) = a₀p₁(r)p₂(r) · · · p_k(r),

donde ningún par de polinomios p₁, p₂, . . . , p_k tiene un factor común y cada uno tiene la forma

p_j(r) = (r − r_j)^m_j,        (9.9.2.12)

donde r_j es real y m_j es un entero positivo, o

p_j(r) = [(r − λ_j)² + ω_j²]^m_j ,        (9.9.2.13)

donde λ_j y ω_j son reales, ω_j ≠ 0 y m_j es un entero positivo. Si se cumple (9.9.2.12), entonces r_j es un cero real de p, mientras que si se cumple (9.9.2.13), entonces λ + iω y λ − iω son ceros conjugados complejos de p. En cualquier caso, m_j es la multiplicidad de los ceros.

        Mediante argumentos similares a los utilizados en nuestros ejemplos, se puede demostrar que

p(D) = a₀p₁(D)p₂(D) · · · p_k(D)        (9.9.2.14)

y que el orden de los factores de la derecha puede elegirse arbitrariamente. Por lo tanto, si p_j(D)y = 0 para algún j entonces p(D)y = 0. Para ver esto, simplemente reescribimos (9.9.2.14) de modo que p_j(D) se aplique primero. Por lo tanto, el problema de encontrar soluciones de p(D)y = 0 con p como en (9.9.2.14) se reduce a encontrar soluciones de cada una de estas ecuaciones

p_j(D)y = 0,  1 ≤ j ≤ k,

donde p_j es una potencia de un término de primer grado o de una cuadrática irreducible. Para encontrar un conjunto fundamental de soluciones {y₁, y₂, . . ., y_n} de p(D)y = 0, encontramos el conjunto fundamental de soluciones de cada una de las ecuaciones y tomamos {y₁, y₂, . . ., y_n} como el conjunto de todas las funciones en estos conjuntos fundamentales separados. En el ejercicio 40 bosquejamos la prueba de que {y₁, y₂, . . ., y_n} es linealmente independiente y, por tanto, un conjunto fundamental de soluciones de p(D)y = 0.

        Para aplicar este procedimiento a ecuaciones generales homogéneas de coeficientes constantes, debemos poder encontrar conjuntos fundamentales de soluciones de ecuaciones de la forma

(D − a)^m y = 0

y

[(D − λ)² + ω²]^m y = 0,

donde m es un número entero positivo arbitrario. Los dos teoremas siguientes muestran cómo hacer esto.

Teorema 9.9.2.1

Si m es un entero positivo, entonces

{e^ax, xe^ax, . . ., x^{m − 1}e^ax}         (9.9.2.15)

es un conjunto fundamental de soluciones de

(D − a)^m y = 0.         (9.9.2.16)  ♦

Prueba:

Demostraremos que si

f (x) = c₁ + c₂x + · · · + c_mx^{m − 1}

es un polinomio arbitrario de grado ≤ m − 1, entonces y = e^axf es una solución de (9.9.2.16). Primero tenga en cuenta que si g es cualquier función diferenciable, entonces

(D − a)e^axg = De^axg − ae^axg = ae^axg + e^axg′ − ae^axg,

por lo que

(D − a)e^axg = e^axg′.         (9.9.2.17)

Por lo tanto

Como f ^(m) = 0, la última ecuación implica que y = e^axf es una solución de (9.9.2.16) si f es cualquier polinomio de grado ≤ m − 1. En particular, cada función en (9.9.2.15) es una solución de (9.9.2.16). Para ver que (9.9.2.15) es linealmente independiente (y por lo tanto un conjunto fundamental de soluciones de (9.9.2.16)), observe que si

c₁e^ax + c₂xe^ax + · · · + c_{m − 1}x^{m − 1}e^ax = 0

para todo x en algún intervalo (a, b), entonces

c₁ + c₂x + · · · + c_{m − 1}x^{m − 1} = 0

para todo x en (a, b). Sin embargo, sabemos por álgebra que si este polinomio tiene más de m − 1 ceros entonces c₁ = c₂ = · · · = c_n = 0. ♦

Ejemplo ilustrativo 9.9.2.5

Encuentre la solución general de

y′′′ + 3y′′ + 3y′ + y = 0.        (9.9.2.18)

Solución:

El polinomio característico de (9.9.2.18) es

p(r) = r³ + 3r² + 3r + 1 = (r + 1)³.

Por lo tanto (9.9.2.18) se puede escribir como

(D + 1)³y = 0,

entonces el Teorema 9.9.2.1 implica que la solución general de (9.9.2.18) es

y = e^−x(c₁ + c₂x + c₃x²). ♦

La demostración del siguiente teorema se esboza en el ejercicio 41.

Teorema 9.9.2.2

Si ω ≠ 0 y m es un entero positivo, entonces

{e^λx cosωx, xe^λx cosωx, . . ., x_{m − 1}e^λx cosωx, e^λx senωx, xe^λx senωx, . . ., x_{m − 1}e^λx senωx}

es un conjunto fundamental de soluciones de

[(D − λ)² + ω²]^my = 0. ♦

Ejemplo ilustrativo 9.9.2.6

Encuentre la solución general de

(D² + 4D + 13)³y = 0.        (9.9.2.19)

Soución:

El polinomio característico de (9.9.2.19) es

p(r) = (r² + 4r + 13)³ = (r + 2)² + 9)³ .

Por lo tanto (9.9.2.19) se puede escribir como

[(D + 2)² + 9]³y = 0,

entonces el Teorema 9.9.2.2 implica que la solución general de (9.9.2.19) es

y = (a₁ + a₂x + a₃x²)e^−2x cos3x + (b₁ + b₂x + b₃x²)e^−2x sen3x. ♦

Ejemplo ilustrativo 9.9.2.7

Encuentre la solución general de 

y⁽⁴⁾ + 4y′′′ + 6y′′ + 4y′ = 0.         (9.9.2.20)

Solución:

El polinomio característico de (9.9.2.20) es

Por lo tanto (9.9.2.20) se puede escribir como

[(D + 1)² + 1](D + 2)Dy = 0.

Conjuntos fundamentales de soluciones de

[(D + 1)² + 1] y = 0, (D + 2)y = 0  y  Dy = 0.

están dados por

{e^−x cosx, e^−x senx}, {e^−2x} y {1},

respectivamente. Por tanto la solución general de (9.9.2.20) es

y = e^−x(c₁ cosx + c₂ senx) + c₃e^−2x + c₄. ♦

Ejemplo ilustrativo 9.9.2.8

Encuentre un conjunto fundamental de soluciones de

[(D + 1)² + 1]²(D − 1)³(D + 1)D²y = 0.         (9.9.2.21)

Solución:

Se puede obtener un conjunto fundamental de soluciones de (9.9.2.21) combinando conjuntos fundamentales de soluciones de

Los conjuntos fundamentales de soluciones de estas ecuaciones están dados por

respectivamente. Estas diez funciones forman un conjunto fundamental de soluciones de (9.9.2.21). ♦